11  Cópulas

Hasta el momento hemos visto como construir modelos univariados. Pero existen aplicaciones donde dos riesgos están correlacionados.

Es decir, a partir de la correlación lineal $\rho$ entre dos variables $X$ y $Y$, podríamos describir su comportamiento. Sin embargo, en pérdidas nos interesa responder otras preguntas:

• Si un riesgo tiene una pérdida muy grande, ¿es más probable que otro riesgo también tenga una pérdida grande?
• ¿Cuáles son las probabilidades de tener varias pérdidas grandes de diferentes tipos de riesgo?

Estas preguntas se responde a partir del concepto de dependencia en las colas construida a partir de la cópula.

11.1 Definición y construcción de cópulas

El concepto de cópula es una distribución generada a partir de las distribuciones marginales de dos o más variables. Formalmente

Una cópula es una función $C:[0,1{]}^d\mapsto [0,1]$ con las siguientes propiedades:

• Marginales:. Para cualquier $j=1,\cdots ,d$ se tiene que $C(1,\dots ,1,u_j,1,\dots ,1)=u_j$.
• Isotónica: $C(u)\le C(v)$ si $u\le v$, donde $u\le v$ significa que $u_j\le v_j$ para todo $j=1,\cdots ,d$.
• $d$-creciente: para cualquier caja $[a,b]\subset [0,1{]}^d$ con volumen no vacío, $C([a,b])>0$.

En particular una cópula $C$ con $d$-variable es la función de distribución conjunta de $d$ variables aleatorias uniformes $(0,1)$. Si etiquetamos las variables aleatorias $d$ como $U_1,U_2,\dots ,U_d$, entonces podemos escribir la cópula $C$ como

$$C(u_1,\dots ,u_d)=\mathrm{Pr}(U_1\le u_1,\dots ,U_d\le u_d).$$

Ahora considere cualquier variable aleatoria continua $X_1,X_2,\dots ,X_d$ con funciones de distribución $F_1,F_2,\dots ,F_d$, respectivamente.

Construya una función de distribución multivariada de la siguiente manera:

$$\begin{array}{rl}F(x_1,\dots ,x_d)& =C[F_1\left(x_1\right),\dots ,F_d\left(x_d\right)]\\ & =\mathrm{Pr}(U_1\le F_1\left(x_1\right),\dots ,U_d\le F_d\left(x_d\right)).\end{array}$$

Primero hay que verificar dos cosas

$F$ es una función de distribución.

Prueba. Note que cada argumento es no decreciente ya que conforme crece cada $x_i$ la función $F_i(x_i)$ correspondiente no decrece (por ser una distribución). Como la función $C$ fue construida a partir de la definición de una distribución conjunta, entonces $F$ también lo es.

Note que el Teorema 11.1 (Sklar) nos dice que siempre se puede construir esta función $C$ a partir de las distribuciones marginales y que esta es única.

Teorema 11.1 (Teorema de Sklar) Para un vector aleatorio $X$ con distribución $F$ y marginales univariadas $F_1,\cdots ,F_d$. Existe una cópula $C$ tal que $$F(x_1,\cdots ,x_d)=C(F_1\left(x_1\right),\cdots ,F_d\left(x_d\right)).$$ Si $X$ es continua, entonces tal cópula $C$ es única.

Las marginales de $F$ son también funciones de distribución.

Prueba. Para una variable $X_1$ se tiene que: $$\begin{array}{rl}\mathrm{Pr}(X_1\le x_1)& =F(x_1,\mathrm{\infty },\dots ,\mathrm{\infty })\\ & =\mathrm{Pr}[U_1\le F_1\left(x_1\right),U_2\le F_2(\mathrm{\infty }),\dots ,U_d\le F_d(\mathrm{\infty })]\\ & =\mathrm{Pr}[U_1\le F_1\left(x_1\right),U_2\le 1,\dots ,U_d\le 1]\\ & =\mathrm{Pr}[U_1\le F_1\left(x_1\right)]\\ & =F_1\left(x_1\right)\end{array}$$

Las ventajas de usar cópulas es que en un problema podemos reconocer el riesgo individual y que este está ligado con otros. Pero no tenemos idea como. El Teorema 11.1 nos dice que podemos experimentar con los riesgos individuales para constuir ese riesgo conjunto desconocido.

11.2 Medidas de asociación

La forma más sencilla de construir una cópula es basado en su correlación

11.2.1 $\rho$ de Spearman

Para dos variables aleatoarios $(X_1,X_2)$, esta cópula se define como

$${\rho }_S(X_1,X_2)=\rho (F_1\left(X_1\right),F_2\left(X_2\right)),$$

donde $\rho$ es la correlación lineal clásica.

Si recordamos que la distribución es una variable uniforme $(0,1)$ con media 1/2 y varianza 1/12 entonces:

$$\begin{array}{rl}{\rho }_S(X_1,X_2)& =\frac{\mathrm{E}\left[F_1\left(X_1\right)F_2\left(X_2\right)\right]-\mathrm{E}\left[F_1\left(X_1\right)\right]\mathrm{E}\left[F_2\left(X_2\right)\right]}{\sqrt{\mathrm{Var}\left(F_1\left(X_1\right)\right)\mathrm{Var}\left(F_2\left(X_2\right)\right)}}\\ & =12\mathrm{E}\left[F_1\left(X_1\right)F_2\left(X_2\right)\right]-3.\end{array}$$

Más concretamente, la $\rho$ de Spearman se puede escribir como $$\begin{array}{rl}{\rho }_S(X_1,X_2)& =12\mathrm{E}[UV]-3\\ & =12{\int }_0^1{\int }_0^{1}uvdC(u,v)-3\\ & =12{\int }_0^1{\int }_0^{1}C(u,v)dudv-3.\end{array}$$

Ejercicio 11.1 Muestre que $${\int }_0^1{\int }_0^{1}uvdC(u,v)={\int }_0^1{\int }_0^{1}C(u,v)dudv.$$ usando integración por partes.

11.2.2 $\tau$ de Kendall

Considere dos variables aleatorias bivariadas continuas independientes e idénticamente distribuidas $(X_1,X_2)$ y $(X_1^{\ast },X_2^{\ast })$ con distribución marginal $F_1(x_1)$ para $X_1$ y $X_1^{\ast }$ y distribución marginal $F_2\left(x_2\right)$ para $X_2$ y $X_2^{\ast }$.

La medida de asociación, de la $\tau$ de Kendall, ${\tau }_K(X_1,X_2)$, está dada por $${\tau }_K(X_1,X_2)=\mathrm{Pr}[(X_1-X_1^{\ast })(X_2-X_2^{\ast })>0]-\mathrm{Pr}[(X_1-X_1^{\ast })(X_2-X_2^{\ast })<0]$$

Es claro que esta medida se puede reescribir como $${\tau }_K(X_1,X_2)=\mathrm{E}\left[\mathrm{sign}(X_1-X_1^{\ast })(X_2-X_2^{\ast })\right].$$

Además se puede reescribir como función de la cópula misma

$$\begin{array}{rl}{\tau }_K(X_1,X_2)& =4{\int }_0^1{\int }_0^{1}C(u,v)dC(u,v)-1\\ & =4\mathrm{E}[C(U,V)]-1.\end{array}$$

Ejercicio 11.2 Pruebe la igualdad anterior haciendo lo siguiente:

1. Recuerde que $\mathrm{Pr}[(X_1-X_1^{\ast })(X_2-X_2^{\ast })<0]=1-\mathrm{Pr}[(X_1-X_1^{\ast })(X_2-X_2^{\ast })>0]$
2. Separe en dos probabilidades distintas $\mathrm{Pr}[(X_1-X_1^{\ast })(X_2-X_2^{\ast })>0]$.
3. Reconstruya cada termino en terminos de $C$.

Si la cópula es absolutamente continua, entonces la ecuación anterior se puede reescribir como $${\tau }_K(X_1,X_2)=4{\int }_0^1{\int }_0^{1}C(u,v)c(u,v)dudv-1$$

donde $c(u,v)=\frac{{\partial }^{2}C(u,v)}{\partial u\partial v}$ es la función de densidad.

11.3 Dependencia en las colas

El interés de construir estos objetos es en caso de que haya pérdidas grandes en una variable, entonces reconocer que también lo existe en las otras.

Considere dos variables aleatorias continuas $X$ y $Y$ con distribuciones marginales $F(x)$ y $G(y)$. El índice de dependencia de la cola superior ${\lambda }_U$ se define como:

$${\lambda }_U=\underset{u\to 1}{lim}\mathrm{Pr}[X>F^{-1}(u)\mid Y>G^{-1}(u)].$$

En resumen, si $X$ es muy grande, dado que $Y$ lo es, entonces podemos identificar cierta dependencia.

Podemos reescribir esta igualdad como

$$\begin{array}{rl}{\lambda }_U& =\underset{u\to 1}{lim}\mathrm{Pr}[F(X)>u\mid G(Y)>u]\\ & =\underset{u\to 1}{lim}\mathrm{Pr}[U>u\mid V>u]\end{array}$$

Haciendo un poco más de álgebra se puede escribir así (¿por qué?):

$$\begin{array}{rl}{\lambda }_U& =\underset{u\to 1}{lim}\frac{1-\mathrm{Pr}(U\le u)-\mathrm{Pr}(V\le u)+\mathrm{Pr}(U\le u,V\le u)}{1-\mathrm{Pr}(V\le u)}\\ & =\underset{u\to 1}{lim}\frac{1-2u+C(u,u)}{1-u}\end{array}$$

De acá observamos que la dependencia de las colas puede ser explicada completamente partir de la cópula y no de las distribuciones marginales.

11.4 Generación de cópulas

El punto clave en la discusión de modelos de cópulas es la construcción de la función $C(u,v)$. En esta sección veremos algunas formas de construirla.

11.4.1 Cópulas arquimedianas

La forma de esta cópula es,

$$C(u_1,\dots ,u_d)={\varphi }^{-1}[\varphi \left(u_1\right)+\cdots +\varphi \left(u_d\right)],$$ donde $\varphi (x)$ es llamado generador.

Propiedades de un generador

• Es una función estrictamente decreciente, convexa y continua.
• Se tiene que $\varphi :[0,1]\to [0,\mathrm{\infty }]$.
• $\varphi (1)=0$.
• La inversa del generador ${\varphi }^{-1}(t)$ debe ser completamente monótona en $[0,\mathrm{\infty }]$. Es decir debe cumplir que $$(-1{)}^n\frac{d^n}{d{x}^n}{\varphi }^{-1}(x)\ge 0,n=1,2,3,\dots$$

Para el caso de dos variables, se puede describir,

• ${\tau }_K$ de kendall: Haciendo los respectivos cálculos se tiene que
  $${\tau }_K(X_1,X_2)=1+4{\int }_0^t\frac{\varphi (u)}{{\varphi }^{\prime }(u)}du.$$

• Dependencia de la colas: $$\begin{array}{rl}\lambda & =\underset{u\to 1}{lim}\frac{1-2u+C(u,u)}{1-u}\\ & =\underset{u\to 1}{lim}\frac{1-2u+{\varphi }^{-1}[2\varphi (u)]}{1-u}\\ & =2-2\underset{t\to 0}{lim}\frac{\frac{d}{dt}{\varphi }^{-1}(2t)}{\frac{d}{dx}{\varphi }^{-1}(t)}\end{array}$$ con la condición que $\underset{t\to 0}{lim}\frac{d}{dt}dt{\varphi }^{-1}(t)=-\mathrm{\infty }$.

Ejercicio 11.3 Prueben esta propiedad usando el teorema de l’Hopital.

11.4.2 Cópulas independientes

Una caso particular de las arquimedianas es cuando $\varphi (u)=-\ln (u)$. Acá se obtiene que

$$C(u_1,\dots ,u_d)=\prod _{j=1}^d{u}_j$$

Ejercicio 11.4 Para este caso en el caso de dos variables se tiene que

• ${\tau }_K=0$.
• ${\lambda }_U=0$.

¿Por qué se da este fenómeno?

11.4.3 Cópula de Gumbel

Usando $\varphi (u)=(-\ln u{)}^{\theta },\theta \ge 1$ se obtiene

$$C(u_1,\dots ,u_d)=\exp \{-{[{(-\ln u_1)}^{\theta }+\cdots +{(-\ln u_d)}^{\theta }]}^{1/\theta }\}$$

En este caso se debe ajustar el parametro $\theta$.

Ejercicio 11.5 Para este caso en el caso de dos variables se tiene que

• ${\tau }_K=1-\frac{1}{\theta }$.
• ${\lambda }_U=2-2^{\frac{1}{\theta }}$.

11.4.4 Otras cópulas

Nombre	Generador	$C(u_1,\dots ,u_d)$	${\lambda }_U$
Joe	$-\ln [1-(1-u{)}^{\theta }],\theta \ge 1$	$1-{[\sum _{j=1}^d{(1-u_j)}^{\theta }-\prod _{j=1}^d{(1-u_j)}^{\theta }]}^{1/\theta }$	$2-2^{\frac{1}{\theta }}$
BB1	${(u^{-5}-1)}^{\theta },\delta >0,\theta \ge 1$	${\{1+{\left[\sum _{j=1}^d{(u_j^{-\delta }-1)}^{\theta }\right]}^{1/\theta }\}}^{-1/\delta }$	$2-2^{1/(\delta \theta )}$

11.5 Cópulas elípticas

Estas son generadas principalmente por distribuciones elípticas.

11.5.1 Cópula gaussiana

$$C(u_1,\dots ,u_d)={\mathrm{\Phi }}_{\mathbf{P}}({\mathrm{\Phi }}^{-1}\left(u_1\right),\dots ,{\mathrm{\Phi }}^{-1}\left(u_d\right))$$

donde $\mathrm{\Phi }(x)$ es la cdf normal univariada estándar y ${\mathbf{\Phi }}_{\mathbf{P}}(x_1,\dots ,x_d)$ es la cdf multivariada de la distribución normal multivariada estándar (con media cero y varianza de 1 para cada componente) y matriz de correlación $\mathbf{P}$. Debido a que la matriz de correlación contiene $d(d-1)/2$ correlaciones por pares, este es el número de parámetros en la cópula.

No existe una forma cerrada simple para la cópula. En el caso bidimensional (con un solo elemento de correlación $\rho$ ), la cópula gaussiana se puede escribir como $$C(u_1,u_2)={\int }_{-\mathrm{\infty }}^{{\mathrm{\Phi }}^{-1}\left(u_1\right)}{\int }_{-\mathrm{\infty }}^{{\mathrm{\Phi }}^{-1}\left(u_2\right)}\frac{1}{2\pi \sqrt{1-{\rho }^2}}\exp \{-\frac{x^2-2\rho xy+y^2}{2(1-{\rho }^2)}\}dydx$$

Aunque su forma teórica es algo difícil de construir, es muy fácil de simular.

Para dos variable se tiene que $${\tau }_K(X_1,X_2)=\frac{2}{\pi }\arcsin (\rho )$$ si $\rho =0$ entonces se obtiene la cópula independiente.

Además, ${\lambda }_U=0$ por lo que esta cópula no es adecuada para modelado de riesgo por este motivo.

11.5.2 Cópula $t$-student

La cópula $t$ viene dada por $$C(u_1,\dots ,u_d)={\mathbf{t}}_{\nu ,\mathbf{P}}(t_{\nu }^{-1}\left(u_1\right),\dots ,t_{\nu }^{-1}\left(u_d\right)),$$ donde $t_{\nu }(x)$ es el cdf de la distribución estándar $t$ con $\nu$ grados de libertad y ${\mathbf{t}}_{\nu ,\mathbf{P}}(x_1,\dots ,x_d)$ es la cdf conjunta de la distribución estándar multivariada $t$ con $\nu$ grados de libertad para cada componente y donde $\mathbf{P}$ es una matriz de correlación. En el caso bidimensional (con un solo elemento de correlación $\rho$ ), la cópula $t$ se puede escribir como$$C(u_1,u_2)={\int }_{-\mathrm{\infty }}^{t_{\nu }^{-1}\left(u_1\right)}{\int }_{-\mathrm{\infty }}^{t_{\nu }^{-1}\left(u_2\right)}\frac{1}{2\pi \sqrt{1-{\rho }^2}}{\{1+\frac{x^2-2\rho xy+y^2}{\nu (1-{\rho }^2)}\}}^{-1-\frac{\nu }{2}}dydx.$$

Se puede estimar que $${\tau }_K(X_1,X_2)=\frac{2}{\pi }\arcsin \rho$$ pero si $\rho =0$ no implica la cópula independiente.

Para este caso, $${\lambda }_U=2t_{\nu +1}(-\sqrt{\frac{1-\rho }{1+\rho }(\nu +1)}).$$

11.6 Laboratorio

Para este ejercicio vamos a usar el siguiente paquete

library(copula)
set.seed(123)

1. Abra la ayuda en la función ellipCopula y describa que tipo de entradas se necesita y que objeto voy a obtener.
2. Construya una cópula gauassiana, de dimensión 3 y $\rho =0.4$. Use getSigma para ver la matriz de correlación.
3. Haga lo mismo con cópula $t$ con 8 df, pero use dispstr='toep' y param = c(0.8, 0.5). Qué ocurrió?
4. Finalmente use la función archmCopula y construya una cópula gumbel con parámetro 3.

Ejercicio 11.6 En este ejemplo se generarán datos que tengan marginales Gamma con una cópula elíptica.

CopulaModelo <-
  mvdc(
    copula = ellipCopula(family = "normal", param = 0.5),
    margins = c("gamma", "gamma"),
    paramMargins = list(list(shape = 2, scale = 1), list(shape = 3, scale = 2))
  )

contour(CopulaModelo, dMvdc, xlim = c(-1, 6), ylim = c(-1, 14))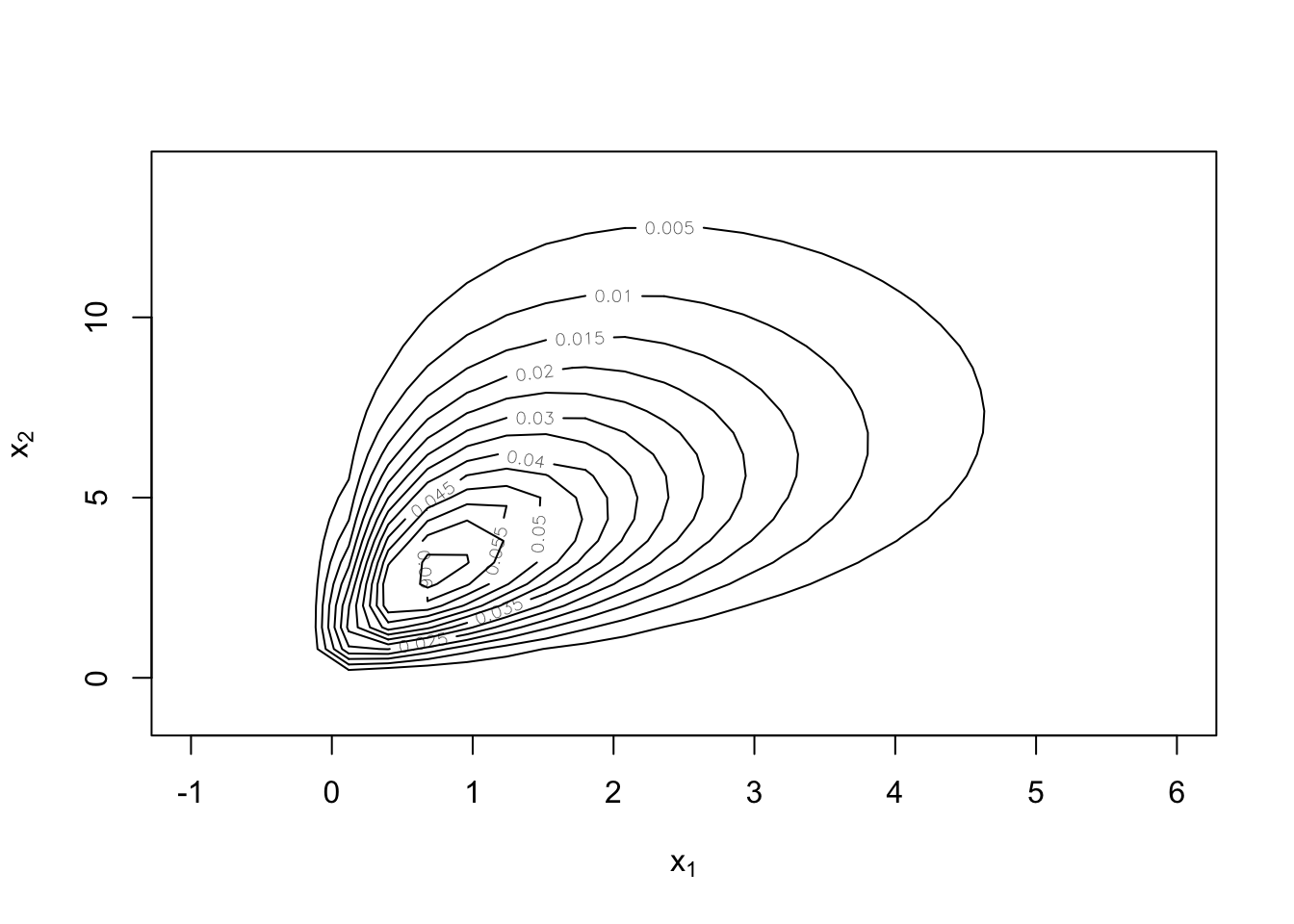

n <- 1000
dat <- rMvdc(mvdc = CopulaModelo, n = n)

1. Cuál es la fórmula exacta para calcular los parámetros shape y scale usando los datos.

2. Construya la ${\tau }_K$ para estos datos

3. Use la función fitMvdc para ajustar la cópula sin valores iniciales. ¿Qué parámetros necesita?
4. Usando los valores iniciales calculados anteriormente vuelva a hacer el ajuste.
5. Vuelva a dibujar la copula, pero usando los valores ajustados del punto anterior.

11.7 Cópulas de valor extremo

Una cópula de este tipo tiene la propiedad de tener estabilidad en el máximo. Para entender esta propiedad veamos esta proposición:

Proposición 11.1 Una cópula de valor extremo satisface la igualdad,

$$C(u_1^n,\dots ,u_d^n)=C^n(u_1,\dots ,u_d),$$

para todo $(u_1,\dots ,u_d)$ y para todo $n\ge 0$.

Prueba. Para demostrar esta propiedad, considere el caso bivariado. Supongamos que $(X_1,Y_1),(X_2,Y_2),\dots ,(X_n,Y_n)$ son $n$ pares aleatorios independientes e idénticamente distribuidos extraídas de la distribución conjunta $F(x,y)$, con distribuciones marginales $F_X(x)$ y $F_Y(y)$ y cópula $C(x,y)$.

Sea $M_X=max(X_1,\dots ,X_n)$ y $M_Y=max(Y_1,\dots ,Y_n)$ los máximos por en cada margen.

Entonces la función de distribución del par aleatorio $(M_X,M_Y)$ es $$\begin{array}{rl}\mathrm{Pr}(M_X\le x,M_Y\le y)& =\mathrm{Pr}(X_i\le x,{\mathrm{Y}}_i\le y,\text{ para todo }i)\\ & =F^n(x,y)\end{array}$$

De manera similar, las distribuciones marginales de $M_X$ y $M_Y$ son $F_X^n(x)$ y $F_Y^n(y)$. Entonces, dado que $$F(x,y)=C[F_X(x),F_Y(y)],$$ podemos escribir la distribución conjunta de los máximos como $$\begin{array}{rl}{F}^n(x,y)& =C^n[F_X(x),F_Y(y)]\\ & =C^n\{{[F_X^n(x)]}^{1/n},{[F_Y^n(y)]}^{1/n}\}.\end{array}$$ Por tanto, la cópula de los máximos viene dada por $$C_{max}(u_1,u_2)=C^n(u_1^{1/n},u_2^{1/n})$$ o equivalente, $$C_{max}(u_1^n,u_2^n)=C^n(u_1,u_2).$$

El resultado anterior dice que si $C_{max}$ es del mismo tipo que la cópula original $C$, entonces la cópula tiene la estabilidad del máximo.

En otras palabras, esta propiedad dice la copula asociados con $(M_X,M_Y)$ es la misma que $C(x,y)$

Se puede probar que la forma general de estas cópulas es

$$C(u_1,u_2)=\exp \{\ln \left(u_1{u}_2\right)A\left(\frac{\ln u_1}{\ln \left(u_1{u}_2\right)}\right)\},$$

donde $A(w)$ es una función de dependencia,

$$A(w)={\int }_0^{1}max[x(1-w),w(1-x)]dH(x)$$

para cualquier $w\in [0,1]$ y $H$ es una función de distribución sobre $[0,1]$. Resulta que $A(w)$ debe ser una función convexa que satisfaga $$max(w,1-w)\le A(w)\le 1,0<w<1$$ y que cualquier función convexa diferenciable $A(w)$ que satisfaga esta desigualdad puede usarse para construir una cópula. Tenga en cuenta que la cópula de independencia resulta de establecer $A(w)$ en su límite superior $A(w)=1$. En el otro extremo, si $A(w)=max(w,1-w)$, entonces hay correlación perfecta y, por tanto, dependencia perfecta con $C(u,u)=u$.

La dependencia de la cola superior se puede escribir como

$$\begin{array}{rl}{\lambda }_U& =\underset{u\to 1}{lim}\frac{1-2u+C(u,u)}{1-u}\\ & =\underset{u\to 1}{lim}\frac{1-2u+u^{2A(1/2)}}{1-u}\\ & =\underset{u\to 1}{lim}2-2A(1/2)u^{2A(1/2)-1}\\ & =2-2A(1/2).\end{array}$$

Algunos ejemplos de este tipo de cópulas son

Nombre	$A(w)$	${\lambda }_U$
Gumbel	${[w^{\theta }+(1-w{)}^{\theta }]}^{1/\theta },\theta \ge 0$	si $w=\frac{1}{2}$ entonces $2-2^{\frac{1}{\theta }}$
Galambos	$1-{[w^{-\theta }+(1-w{)}^{-\theta }]}^{-1/\theta },\theta >0$	$2^{-1/\theta }$

11.7.1 Cópulas Archimax

Combinando cópulas arquimedianas y de valor extremos se puede escribir las siguiente representación,

$$C(u_1,u_2)={\varphi }^{-1}\left[\{\varphi \left(u_1\right)+\varphi \left(u_2\right)\}A\left(\frac{\varphi \left(u_1\right)}{\varphi \left(u_1\right)+\varphi \left(u_2\right)}\right)\right],$$ donde $\varphi (u)$ es un generador arquimediano válido y $A(w)$ es una función de dependencia válida.

Nombre	$\varphi (u)$	$A(w)$	$C(u_1,u_2)$
BB4	$u^{-\theta }-1,\theta \ge 0$	$1-{\{w^{-\delta }+(1-w{)}^{-\delta }\}}^{-1/\delta },\theta >0,\delta >0$	${\{u_1^{-\theta }+u_2^{-\theta }-1-{[{(u_1^{-\theta }-1)}^{-\delta }+{(u_2^{-\theta }-1)}^{-\delta }]}^{-1/\delta }\}}^{-1/\theta }$

11.8 Estimación por máxima verosimilitud

Recuerde que la cópula es de la forma $$F(x_1,\dots ,x_d)=C[F_1\left(x_1\right),\dots ,F_d\left(x_d\right)]$$

y su densidad es $$f(x_1,\dots ,x_d)=f_1\left(x_1\right)f_2\left(x_2\right)\cdots f_d\left(x_d\right)c[F_1\left(x_1\right),\dots ,F_d\left(x_d\right)]$$

Nota

La estimación de los parámetros de la cópula depende de la estimación de las marginales.

Entonces se puede escribir para $n$ datos

$$\begin{array}{rl}l& =\sum _{j=1}^n\ln f(x_{1,j},\dots ,x_{d,j})\\ & =\sum _{j=1}^n\sum _{i=1}^d\ln f_i\left(x_{i,j}\right)+\sum _{j=1}^n\ln c[F_1\left(x_{1,j}\right),\dots ,F_d\left(x_{d,j}\right)]\\ & =l_w+l_c.\end{array}$$

Forma de estimación

1. Optimice las $d$ funciones $\ln (f_i(x_{ij})$ individualmente.
2. Use esos valores para construir los pseudo-verosimiludes ${\tilde{u}}_{i,j}={\tilde{F}}_i\left(x_{i,j}\right)$.
3. Optimice la pseudo-verosimilitud de la cópula ${\tilde{l}}_c=\sum _{j=1}^n\ln c({\tilde{u}}_{1,j},\dots ,{\tilde{u}}_{dj})$.

11.9 Medidas de mejor ajuste

Sabemos que $U_1=F_1\left(X_1\right)$ y $U_2=F_2\left(X_2\right)$ son ambas variables aleatorias uniformes $(0,1)$.

Ahora introduzca las variables aleatorias condicionales $V_1=F_{12}(X_1\mid X_2)$ y $V_2=F_{21}(X_2\mid X_1)$. Entonces, las variables aleatorias $V_1$ y $U_2$ son $(0,1)$ variables aleatorias uniformes mutuamente independientes.

Note que la variable aleatoria $V_1=F_{12}(X_1\mid$ $X_2=x$ ). Debido a que es una distribución aplicada a una variable aleatoria, debe tener una distribución uniforme $(0,1)$. Este resultado es cierto para cualquier valor de $x$. Así, la distribución de $V_1$ no depende del valor de $X_2$ y por tanto no depende de $U_2=F_2\left(X_2\right)$.

El valor observado de la función de distribución de la variable aleatoria condicional $X_2$ dada $X_1=x_1$ es $$F_{21}(x_2\mid X_1=x_1)=C_1[F_{X_1}\left(x_1\right),F_{X_2}\left(x_2\right)].$$ El valor observado $v_2$ de la variable aleatoria $V_2$ se puede obtener a partir de los valores observados de las variables aleatorias bivariadas $(X_1,X_2)$ de $$v_2={\hat{F}}_{21}(x_2\mid X_1=x_1)={\hat{C}}_1[{\hat{F}}_{X_1}\left(x_1\right),{\hat{F}}_{X_2}\left(x_2\right)].$$ Por lo tanto, podemos generar un conjunto univariado de datos que debería verse como una muestra de una distribución $(0,1)$ uniforme si la combinación de distribuciones marginales y la cópula se ajusta bien a los datos.

El método sugerido para probar el ajuste es el siguiente

Nota

• Paso 1. Ajuste y seleccione las distribuciones marginales utilizando métodos univariados.
• Paso 2. Pruebe la uniformidad de la distribución condicional de $V_1$.
• Paso 3. Pruebe la uniformidad de la distribución condicional de $V_2$.

Las pruebas a usar son las usuales que hemos visto en el curso.

Para más dimensiones, se pueden probar las variables dos a dos y comprobar el ajuste.

11.9.1 Laboratorio

library(copula)
library(tidyverse)

data(loss)
# loss data loss: pérdida de la compañía hasta cierto límite.
# alae: gastos relacionados con el reclamo (gastos legales, gastos por
# investigaciones, etc. )

ggplot(loss, aes(loss, alae)) +
  geom_point()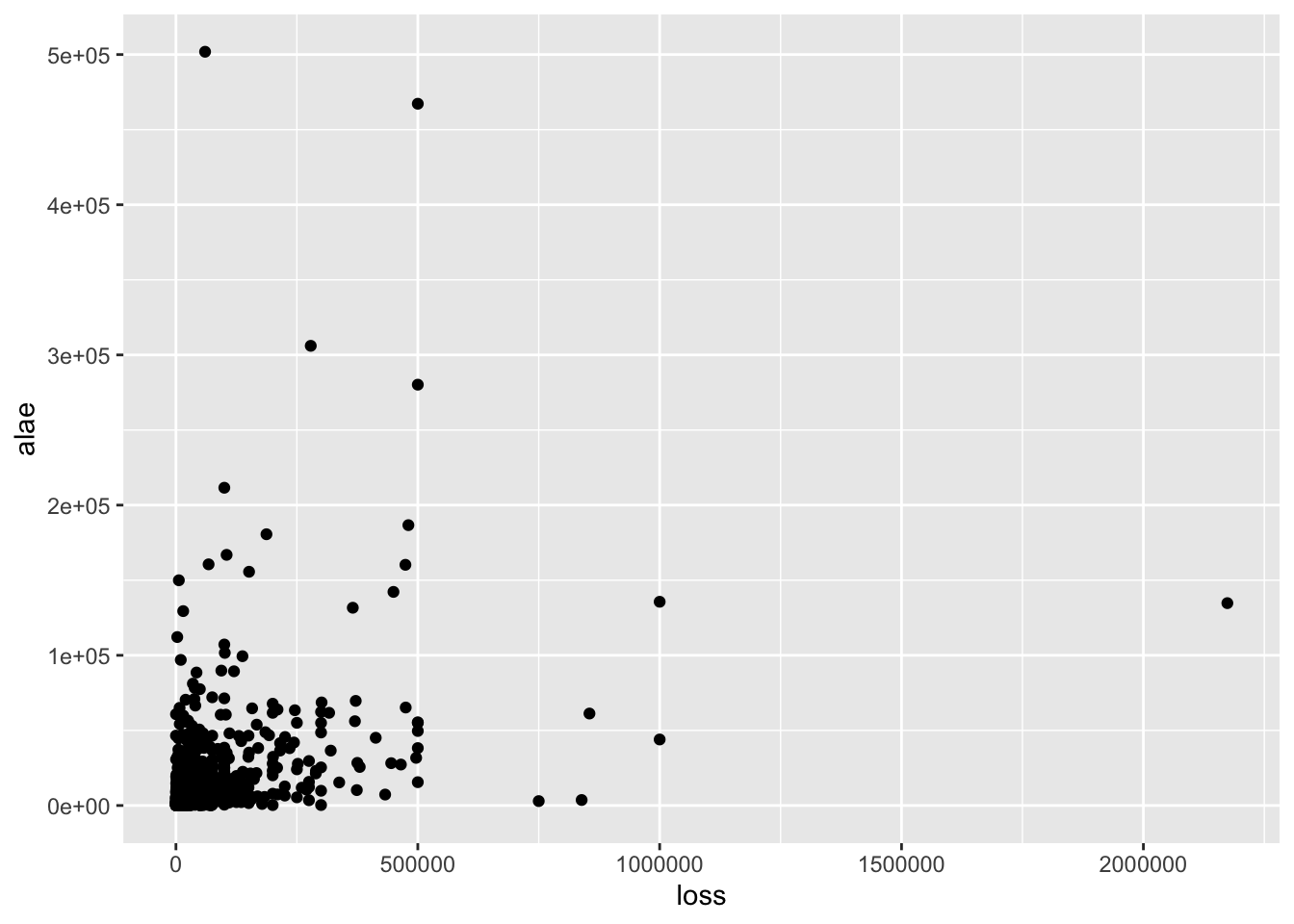

ggplot(loss, aes(log(loss), log(alae))) +
  geom_point()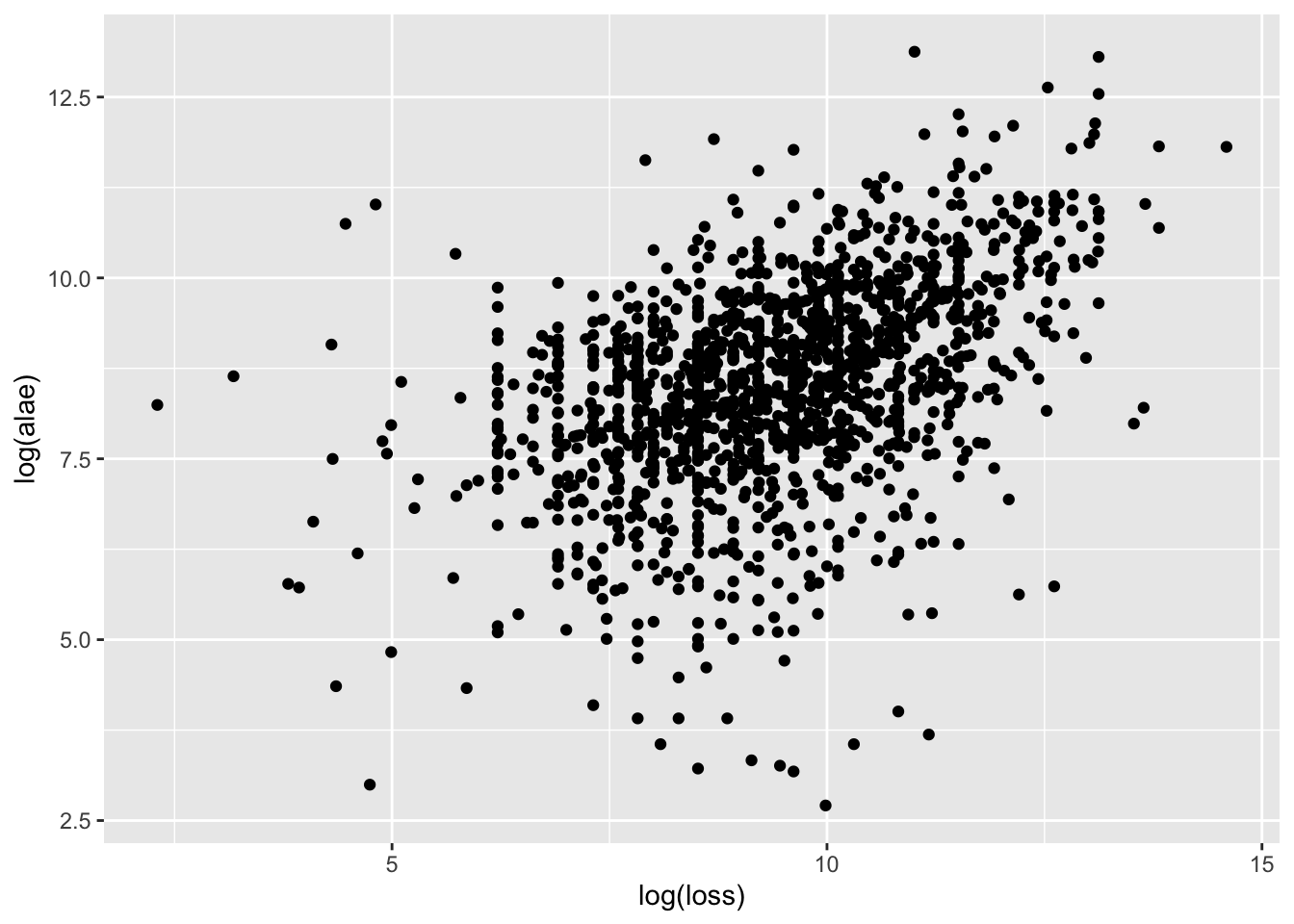

1. Ajuste las variables loss y alae individualmente. Traten Pareto, lognormal, gamma, etc. ¿Cuál es mejor? (Noten que algunos valores están censurados) (usen coef(fit) para obtener los parámetros correctos.)
2. Construya las variables $U_1$ y $U_2$ para cada marginal. Compruebe que la hipotesis de uniformidad se cumple.
3. Use cópulas Frank, Gumbel, Normal y t para modelar la distribución conjunta de $U_1$ y $U_2$. (revise la función archCopula).
4. Use la funciones contour y persp para visualizar la copula.
5. Revisen la tau de Kendall y la dependencia de la cola para caso.
6. Calcule la distribuciones condicionales usando cCopula y verifique el supuesto de uniformidad.
7. Finalmente, calcule el VaR al 95% y 99% de cada margen asumiendo independencia. Usando la función rMvdc genere datos aleatorios de cada margen usando la cópula y calcule los mismos niveles de VaR. Compare los resultados.

11.10 El rol de los deducibles

Cada variable puede tener su propio deducibles y las variables en los margenes podrían ser datos individuales o agrupados. Esto genera diferencias para la construcción del estimador de máxima verosimilitud.

En este caso explicaremos las diferencias en el caso bivariado. Recordemos que

$$\begin{array}{rl}F(x,y)& =C[F_1\left(x_1\right),F_2\left(x_2\right)]\\ f(x,y)& =f_1\left(x_1\right)f_2\left(x_2\right)c[F_1\left(x_1\right),F_2\left(x_2\right)]\end{array}$$

donde $$\begin{array}{rl}{C}_1(u_1,u_2)& =\frac{\partial }{\partial u_1}C(u_1,u_2)\\ C_2(u_1,u_2)& =\frac{\partial }{\partial u_2}C(u_1,u_2),\\ c(u_1,u_2)& =C_{12}(u_1,u_2)=\frac{\partial }{\partial u_1}\frac{\partial }{\partial u_2}C(u_1,u_2).\end{array}$$

En el caso de datos agrupados solo hay que considerar el caso cuando el dato cae sobre intervalo. Llamemos $[a_1,b_1]$ y $[a_2,b_2]$ los intervalos respectivos para $X_1$ y $X_2$.

Consideramos cuatro casos:

• Caso #1: Datos individuales para $X_1$ y $X_2$.

  En este caso, se tiene un factor muy similar al visto para el caso univariado. Si $X_1$ o $X_2$ caen por debajo de su deducibles no son tomadas en cuenta.

$$\begin{array}{rl}& \frac{f(x_1,x_2)}{1-F_1\left(d_1\right)-F_2\left(d_2\right)+F(d_1,d_2)}\\ & =\frac{f_1\left(x_1\right)f_2\left(x_2\right)c[F_1\left(x_1\right),F_2\left(x_2\right)]}{1-F_1\left(d_1\right)-F_2\left(d_2\right)+C[F_1\left(d_1\right),F_2\left(d_2\right)]}.\end{array}$$

• Caso #2: Dato individual para $X_1$ y dato agrupado para $X_2$.

  Tenemos lo siguiente

$$\begin{array}{rl}& \frac{\frac{\partial }{\partial x_1}F(x_1,b_2)-\frac{\partial }{\partial x_1}F(x_1,a_2)}{1-F_1\left(d_1\right)-F_2\left(d_2\right)+F(d_1,d_2)}\\ & =\frac{f_1\left(x_1\right)\{C_1[F_1\left(x_1\right),F_2\left(b_2\right)]-C_1[F_1\left(x_1\right),F_2\left(a_2\right)]\}}{1-F_1\left(d_1\right)-F_2\left(d_2\right)+C[F_1\left(d_1\right),F_2\left(d_2\right)]}.\end{array}$$

• Caso #3: Dato individual para $X_2$ y dato agrupado para $X_1$.

  $$\begin{array}{rl}& \frac{\frac{\partial }{\partial x_2}F(b_1,x_2)-\frac{\partial }{\partial x_2}F(a_1,x_2)}{1-F_1\left(d_1\right)-F_2\left(d_2\right)+F(d_1,d_2)}\\ & =\frac{f_2\left(x_2\right)\{C_2[F_1\left(b_1\right),F_2\left(x_2\right)]-C_1[F_1\left(a_1\right),F_2\left(x_2\right)]\}}{1-F_1\left(d_1\right)-F_1\left(d_2\right)+C[F_1\left(d_1\right),F_2\left(d_2\right)]}.\end{array}$$

• Caso #4: Ambos datos agrupados.

  $$\begin{array}{c}\frac{F(b_1,b_2)-F(a_1,b_2)-F(b_1,a_2)+F(a_1,a_2)}{1-F_1\left(d_1\right)-F_2\left(d_2\right)+F(d_1,d_2)}\\ \{C[F_1\left(b_1\right),F_2\left(b_2\right)]-C[F_1\left(a_1\right),F_2\left(b_2\right)]\\ =\frac{-C[F_1\left(b_1\right),F_2\left(a_2\right)]+C[F_1\left(a_1\right),F_2\left(a_2\right)]\}}{1-F_1\left(d_1\right)-F_2\left(d_2\right)+C[F_1\left(d_1\right),F_2\left(d_2\right))]}.\end{array}$$

11.11 Simulación de copulas

Para efectos de análisis de la cópula y las marginales, es necesario definir un proceso para generación de valores aleatorios.

11.11.1 Cópulas Gaussianas

Un vector gaussiano $d$-dimensional tiene la caracteristica de que

$$X=\mu +LZ$$

donde $\mathrm{\Sigma }=L{L}^{\mathrm{\top }}$. Entonces para generar números aleatorios a partir de la cópula se puede hacer lo siguiente:

1. Calcule el factor de Cholesky $L$ de la matriz de correlación $P$.
2. Genera una muestra $Z_1,\dots ,Z_d\stackrel{\text{ ind. }}{\sim }\mathrm{N}(0,1)$.
3. Calcule $\mathit{X}=L\mathit{Z}$.
4. Devuelve $\mathit{U}=(\mathrm{\Phi }\left(X_1\right),\dots ,\mathrm{\Phi }\left(X_d\right))$.

11.11.2 Cópulas $t$

Este caso es similar al gaussiano, salvo una modificación:

1. Calcule el factor de Cholesky $L$ de la matriz de correlación $P$.
2. Genera una muestra $Z_1,\dots ,Z_d\stackrel{\text{ ind. }}{\sim }\mathrm{N}(0,1)$.
3. Genere una muestra $W\sim IG(\frac{\nu }{2},\frac{\nu }{2})$ independiente de $Z$.
4. Calcule $\mathit{X}=\sqrt{W}L\mathit{Z}$.
5. Devuelve $\mathit{U}=(t_{\nu }\left(X_1\right),\dots ,t_{\nu }\left(X_d\right))$.

11.11.3 Cópulas arquimedianas

Para el caso de las arquimedianas, primero hay que definir lo siguiente.

Sea $V$ una variable aleatoria no negativa con distribución $F$. La transformada de Laplace-Stielties de $F$ está definida por $$\mathcal{LS}[F](t)={\int }_0^{\mathrm{\infty }}\exp (-tv)\mathrm{d}F(v)=\mathbb{E}(\exp (-tV)),t\in [0,\mathrm{\infty }).$$

La función $F$ se puede recuperar a partir de la inversa ${\mathcal{LS}}^{-1}[\psi ]$. El uso de esta función es debido al teorema de Bernstein. Este dice que $\psi$ es completamente monótona si y solo si $\psi$ es la transformada de Laplace-Stielties de una distribución $F$ en los reales positivos con $F(0)=0$.

La variable aleatoria $V\sim F$ se cononce como frailty y $F$ es la distribución frailty.

Se puede probar que

$$\mathit{U}=(\psi \left(\frac{E_1}{V}\right),\dots ,\psi \left(\frac{E_d}{V}\right))\sim C$$

donde $E_1,\dots ,E_d\stackrel{\text{ ind }}{\sim }\mathrm{Exp}(1)$ son independientes de$V$.

El algoritmo general es

1. Muestree $V\sim F=\mathcal{L}{\mathcal{S}}^{-1}[\psi ]$.
2. Muestree $E_1,\dots ,E_d\stackrel{\text{ ind }}{\sim }\mathrm{Exp}(1)$, independiente de $V$.
3. Devuelva $\mathit{U}=(\psi \left(E_1/V\right),\dots ,\psi \left(E_d/V\right))$.

11.11.4 Laboratorio

1. Use el algoritmo de construcción de cópulas gaussianas con matrices covarianza $$\left(\begin{array}{cc}16& 4\\ 4& 2\end{array}\right)\left(\begin{array}{cc}1& 0.5\\ 0.5& 1\end{array}\right)$$ Use 1000 valores. Compare ambos resultados.

2. Construya una copula normal asumiendo que la ${\tau }_K=0.5$. Revise la función iTau para encontrar el parámetro correcto.

3. Genere con rCopula y haga el plot de estos resultados. Comparelos con el punto estos resultados. Comparelos con el punto 1.

4. Suponga que se quiere simular una cópula $t$ con 4 grados de libertad. Repita lo puntos 1 a 3 para este caso. W puede simularse como $W=\nu /T$ con $T\sim {\chi }_{\nu }^2$

5. Para 5 variables, ajuste una cópula Gumbel con ${\tau }_K=0.5$. Use iTau de nuevo.

6. Para generar manualmente los valores aleatorios de la cópula se necesita lo siguiente

family = "Gumbel"
cop <- getAcop(family) 
V <- cop@V0(n, theta = parametro_de_iTau) 

Revise la ayuda de acopula. 7. Compare este resultado con rCopula.