fX <- c(0.15, 0.2, 0.25, 0.125, 0.075, 0.05, 0.05, 0.05, 0.025, 0.025)
knitr::kable(cbind(x = 1:10, f_X = fX))| x | f_X |
|---|---|
| 1 | 0.150 |
| 2 | 0.200 |
| 3 | 0.250 |
| 4 | 0.125 |
| 5 | 0.075 |
| 6 | 0.050 |
| 7 | 0.050 |
| 8 | 0.050 |
| 9 | 0.025 |
| 10 | 0.025 |
Una compañía tiene un plan dental para los empleados y sus familias.
Se tiene la distribución de los pagos (en unidades de 25)
fX <- c(0.15, 0.2, 0.25, 0.125, 0.075, 0.05, 0.05, 0.05, 0.025, 0.025)
knitr::kable(cbind(x = 1:10, f_X = fX))| x | f_X |
|---|---|
| 1 | 0.150 |
| 2 | 0.200 |
| 3 | 0.250 |
| 4 | 0.125 |
| 5 | 0.075 |
| 6 | 0.050 |
| 7 | 0.050 |
| 8 | 0.050 |
| 9 | 0.025 |
| 10 | 0.025 |
La distribución de los eventos
pn <- matrix(c(0.05, 0.1, 0.15, 0.2, 0.25, 0.15, 0.06, 0.03, 0.01), nrow = 1)
knitr::kable(cbind(n = 0:8, t(pn)))| n | |
|---|---|
| 0 | 0.05 |
| 1 | 0.10 |
| 2 | 0.15 |
| 3 | 0.20 |
| 4 | 0.25 |
| 5 | 0.15 |
| 6 | 0.06 |
| 7 | 0.03 |
| 8 | 0.01 |
Para entender el siguiente calculo recuerde que necesitamos calcular
\[\begin{equation*} f_S(x)=\sum_{n=0}^8 p_n f_X^{* n}(x) \end{equation*}\]
con los valores iniciales \(f_X^{*0}(x)\) es 1 si \(x=0\) y 0 si \(x\neq 0\). Luego \(f_{X}^{*1}(x)=f_X(x)\).
\[\begin{align*} f_X^{*2}(0) &= 0 \\ f_X^{*2}(1) &= f_X^{*1}(1) f_X^{(0)} + f_X^{*1}(0) f_X^{1}= 0 \\ f_X^{*2}(2) &= f_X^{*1}(2) f_X^{(0)} + f_X^{*1}(1) f_X^{1} + f_X^{*1}(0) f_X^{2}= 0+0.15^2+0= 0.0225 \\ \end{align*}\]
Calcule a mano para \(x=4\), \(f_X^{*3}(x)\), \(f_X^{*4}(x)\) y \(f_X^{*5}(x)\).
El cálculo general sería este
library(tictoc)
ncolumnas <- length(pn) - 1
nfilas <- 200
tabla_convolucion <- matrix(0, nrow = nfilas + 1, ncol = ncolumnas + 1)
tabla_convolucion[1, 1] <- 1
tictoc::tic()
for (nc in 1:ncolumnas) {
for (nf in 1:nfilas) {
s <- 0
for (k in seq_len(min(nf, length(fX)))) {
s <- s + tabla_convolucion[nf - k + 1, nc] * fX[k]
}
tabla_convolucion[nf + 1, nc + 1] <- s
}
}
tictoc::toc()0.022 sec elapsedpn_tabla <- kronecker(matrix(1, nrow = nfilas + 1), pn)
fS <- rowSums(pn_tabla * tabla_convolucion)
plot(0:nfilas, fS, type = "l", xlab = "payment", ylab = "aggregate density")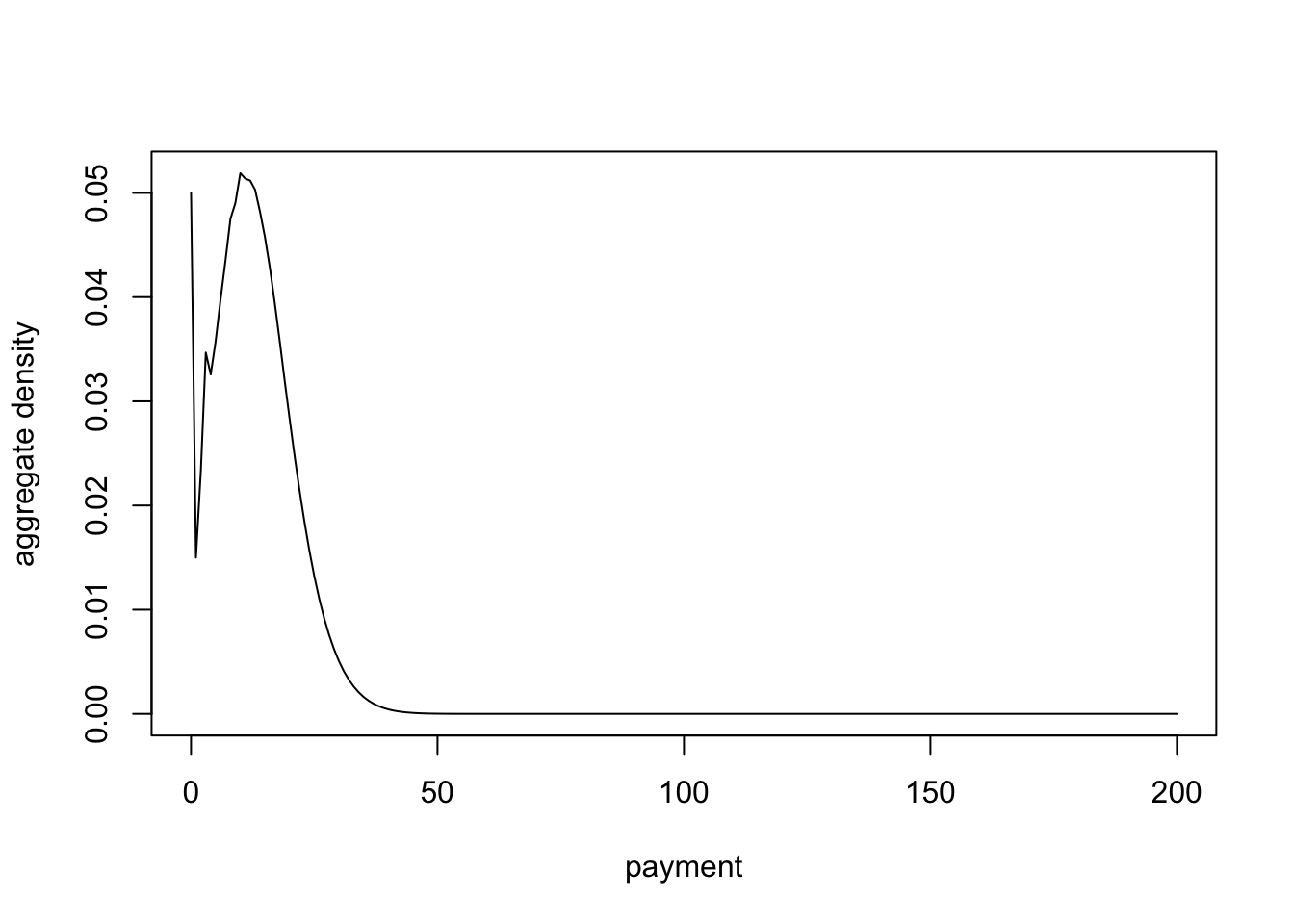
(EN <- sum(pn * (0:ncolumnas)))[1] 3.4(EX <- sum(fX * (1:10)))[1] 3.7(ES <- EN * 25 * EX)[1] 314.5(ES_usando_fS <- 25 * sum((0:nfilas) * fS))[1] 314.5Para esto primero debemos definir la clase de la distribución de conteo.
pn <- as.numeric(pn)
dfpn <- data.frame(k = (1:8), r = (1:8) * pn[2:9] / pn[1:8])
plot(dfpn)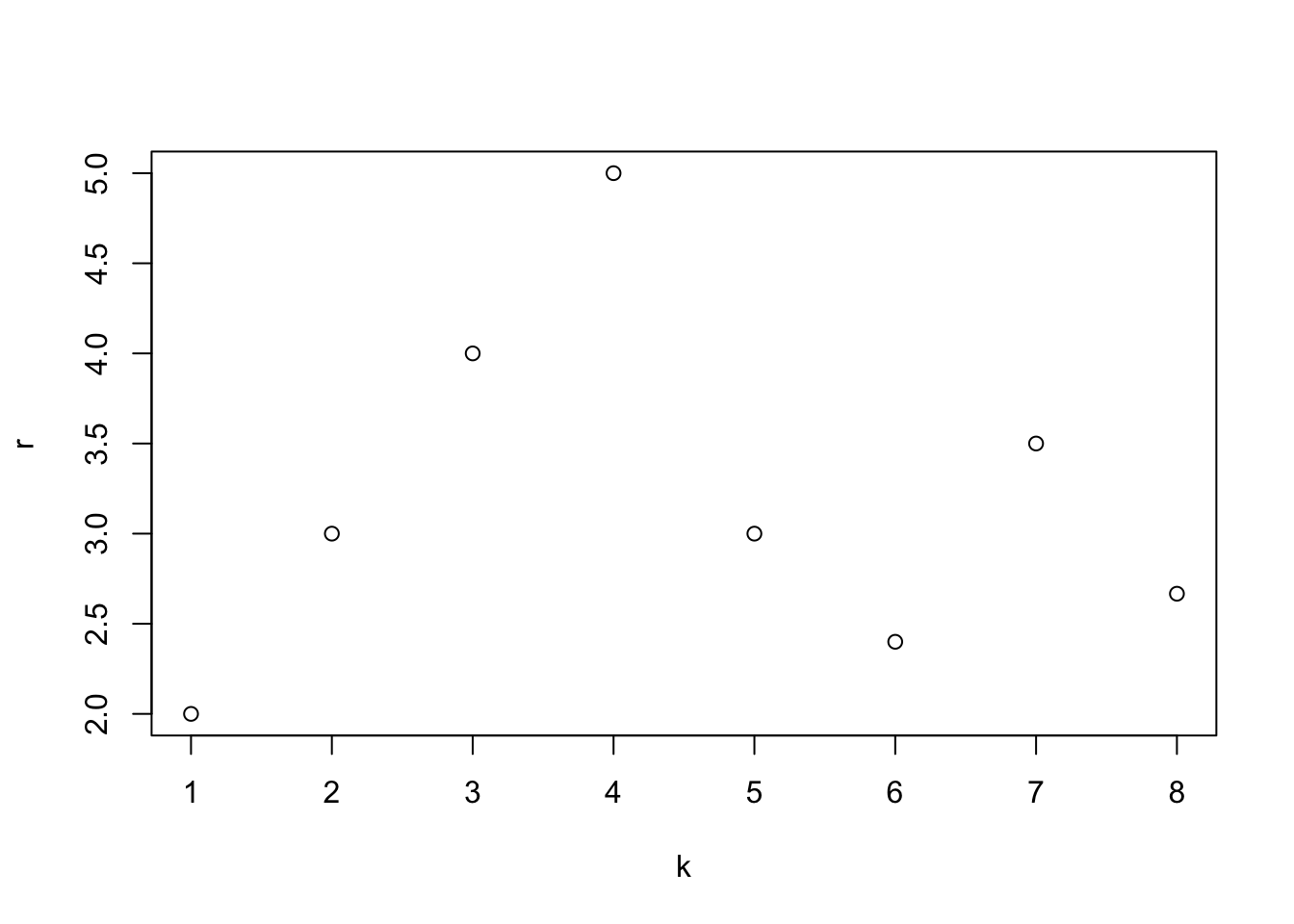
fitpn <- lm(r ~ k, data = dfpn)
fitpn_wo_intercept <- lm(r ~ k - 1, data = dfpn)
dfpn <- cbind(dfpn,
w_intercept = predict(fitpn, newdata = data.frame(k = 1:8)),
wo_intercept = predict(fitpn_wo_intercept, newdata = data.frame(k = 1:8))
)dfpn <- dfpn %>%
pivot_longer(-k)ggplot(dfpn, aes(x = k, y = value, color = name)) +
geom_line()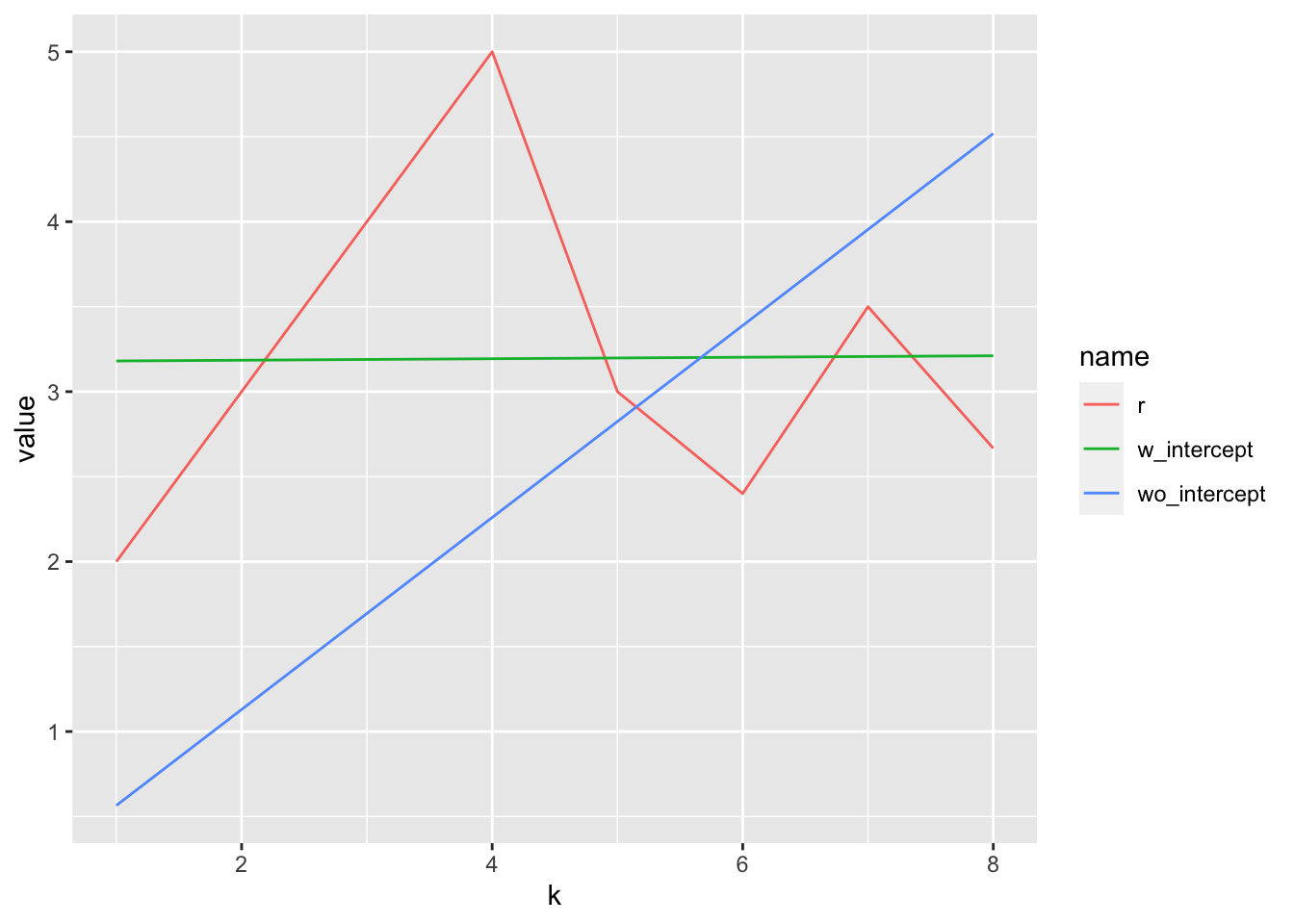
En este caso se está tomando una Poisson de clase \((a,b,0)\) para simplificar el ejemplo. El coeficiente \(b\) es igual a 3.18.
Necesitamos calcular esta recursión
\[\begin{equation*} f_S(x)=\frac{\sum_{y=1}^{x \wedge m}(a+b y / x) f_X(y) f_S(x-y)}{1-a f_X(0)} \end{equation*}\]
donde necesariamente necesitamos el valor de \(f_S(0)=P_N\left[f_X(0)\right]\).
Pruebe que para el caso Poisson el calculo se simplifica a
\[\begin{equation*} f_S(x)=\frac{\lambda}{x} \sum_{y=1}^{x \wedge m} y f_X(y) f_S(x-y), \quad x=1,2, \ldots \end{equation*}\]
con \(f_S(0)=e^{-\lambda\left[1-f_X(0)\right]}\)
Usando el valor de \(b=3.18\) calcule \(f_S(1)\), \(f_S(2)\) y \(f_S(3)\) a mano.
b <- coefficients(fitpn)[1]
lambda <- b
fS_recursive <- exp(-lambda)
tictoc::tic()
for (x in 1:200) {
s <- 0
for (y in 1:10) {
if (x - y >= 0) {
s <- s + y * fX[y] * fS_recursive[x - y + 1]
}
}
fS_recursive[x + 1] <- lambda / x * s
}
tictoc::toc()0.013 sec elapsedES_usando_fS_recursive <- sum((0:nfilas)*fS_recursive)
25*ES_usando_fS_recursive[1] 293.7976ES2_usando_fS_recursive <- sum((0:nfilas)^2*fS_recursive)
sqrt(25^2*(ES2_usando_fS_recursive - ES_usando_fS_recursive^2))[1] 194.4647Note que los valores obtenidos no se acercan a los resultados del ejemplo anterior. Para esto considere cambiar la distribución de la clase \((a,b,0)\) y ver si pueden mejorar los resultados.
Para las severidades continuas se usan dos métodos
Método de rendondeo: Sea \(f_j\) la probabilidad en el punto \(j h, j=0,1,2, \ldots\). Entonces asignamos \[\begin{equation*} \begin{aligned} f_0 &=\operatorname{Pr}\left(X<\frac{h}{2}\right)=F_X\left(\frac{h}{2}-0\right) \\ f_j &=\operatorname{Pr}\left(j h-\frac{h}{2} \leq X<j h+\frac{h}{2}\right) \\ &=F_X\left(j h+\frac{h}{2}-0\right)-F_X\left(j h-\frac{h}{2}-0\right), \quad j=1,2, \ldots . \end{aligned} \end{equation*}\]
Método de los momentos: En este caso se construyen una distribución aritmética de modo que calcen los \(p\)-momentos teórica con los empíricos.
Considere un intervalo arbitrario de longitud \(p h\), denotado por \(\left[x_k, x_k+p h\right)\). Ubicamos las masas puntuales \(m_0^k, m_1^k, \ldots, m_p^k\) en los puntos \(x_k, x_k+h, \ldots, x_k+p h\) de modo que los primeros \(p\) momentos se conservan. El sistema de ecuaciones \(p+1\) que refleja estas condiciones es
\[\begin{equation*} \sum_{j=0}^p\left(x_k+j h\right)^r m_j^k=\int_{x_k^{-}}^{x_k+p h^{-}} x^r d F_X(x), \quad r=0,1,2, \ldots, p \end{equation*}\]
Luego se ordenan los intervalos de modo que \(x_{k+1}=x_k+ph\).
Por ejemplo suponga que \(x_0=0\)
Entonces el sistema de ecuaciones queda
\[\begin{equation*} \sum_{j=0}^p\left(j h\right)^r m_j^0=\int_{0^{-}}^{ph^{-}} x^r d F_X(x), \quad r=0,1,2, \ldots, p \end{equation*}\]
Podemos escribir los puntos de las distribución como
\[\begin{equation*} \begin{array}{lll} f_0=m_0^0, & f_1=m_1^0, & f_2=m_2^0, \ldots \\ f_p=m_p^0+m_0^1, & f_{p+1}=m_1^1, & f_{p+2}=m_2^1, \ldots . \end{array} \end{equation*}\]
\[\begin{equation*} m_j^k=\int_{x_k-0}^{x_k+p h-0} \prod_{i \neq j} \frac{x-x_k-i h}{(j-i) h} d F_X(x), \quad j=0,1, \ldots, p . \end{equation*}\]
Supongamos que \(X\) tiene la distribución exponencial con pdf \(f(x)=0.1 e^{-0.1 x}\). Use un lapso de \(h=2\) para discretizar esta distribución por el método de redondeo y haciendo coincidir el primer momento. Para el método de redondeo, las fórmulas generales son
Para el método del rendondeo las fórmulas son \[\begin{equation*} \begin{array}{l} f_0=F(1)=1-e^{-0.1(1)}=0.09516 \\ f_j=F(2 j+1)-F(2 j-1)=e^{-0.1(2 j-1)}-e^{-0.1(2 j+1)} \end{array} \end{equation*}\]
h <- 0.1
f_redondeo <- pexp(q = 1 , rate = 0.1)
f_redondeo[2:51] <- pexp(q = (h * (1:50)) + 1, rate = 0.1) -
pexp(q = (h * (1:50)) - 1, rate = 0.1)
plot(f_redondeo, type="l")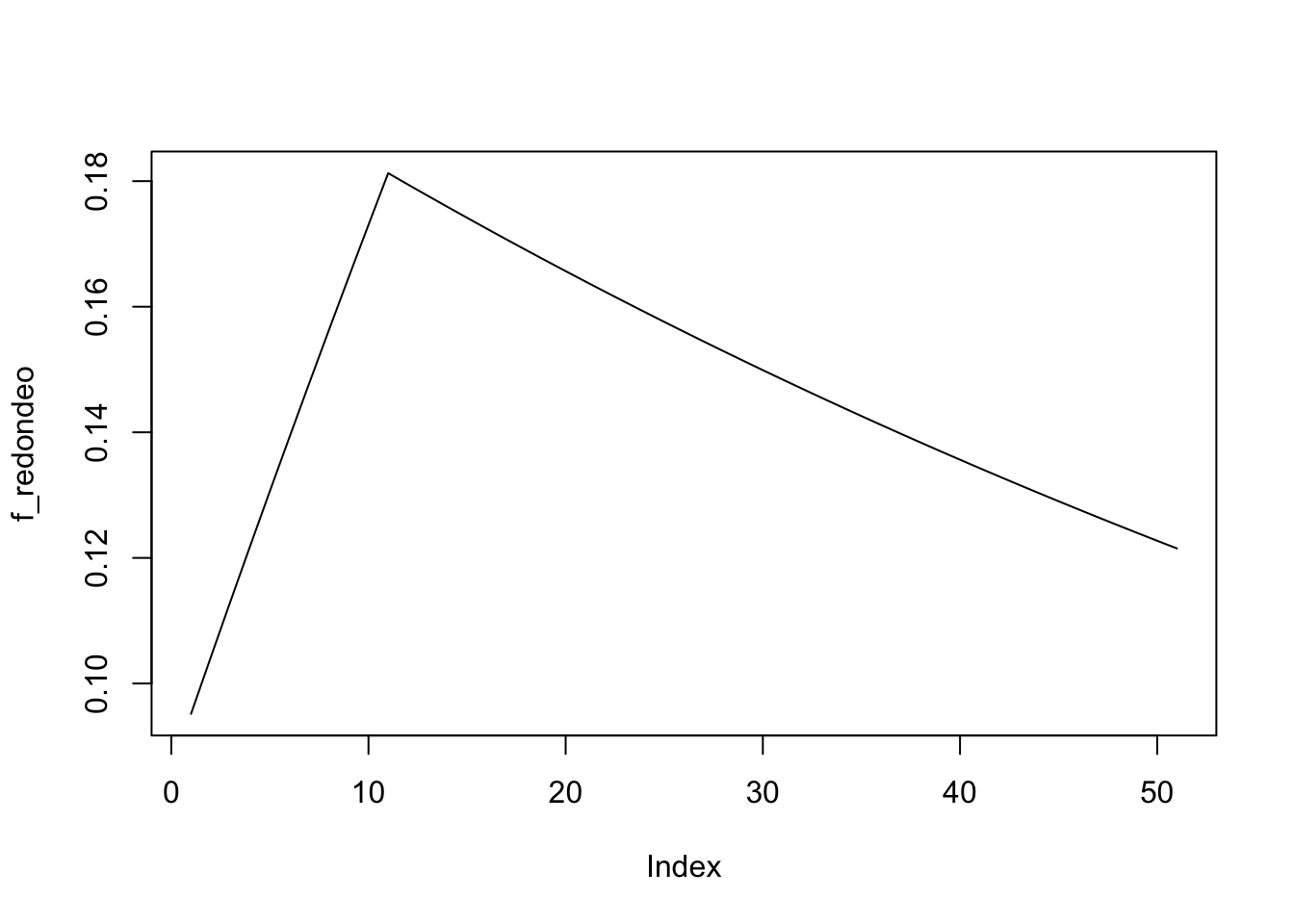
h <- 5
f_redondeo <- pexp(q = 1 , rate = 0.1)
f_redondeo[2:51] <- pexp(q = (h * (1:50)) + 1, rate = 0.1) -
pexp(q = (h * (1:50)) - 1, rate = 0.1)
plot(f_redondeo, type="l")
h <- 2
f_redondeo <- pexp(q = 1 , rate = 0.1)
f_redondeo[2:51] <- pexp(q = (h * (1:50)) + 1, rate = 0.1) -
pexp(q = (h * (1:50)) - 1, rate = 0.1)
plot(f_redondeo, type="l")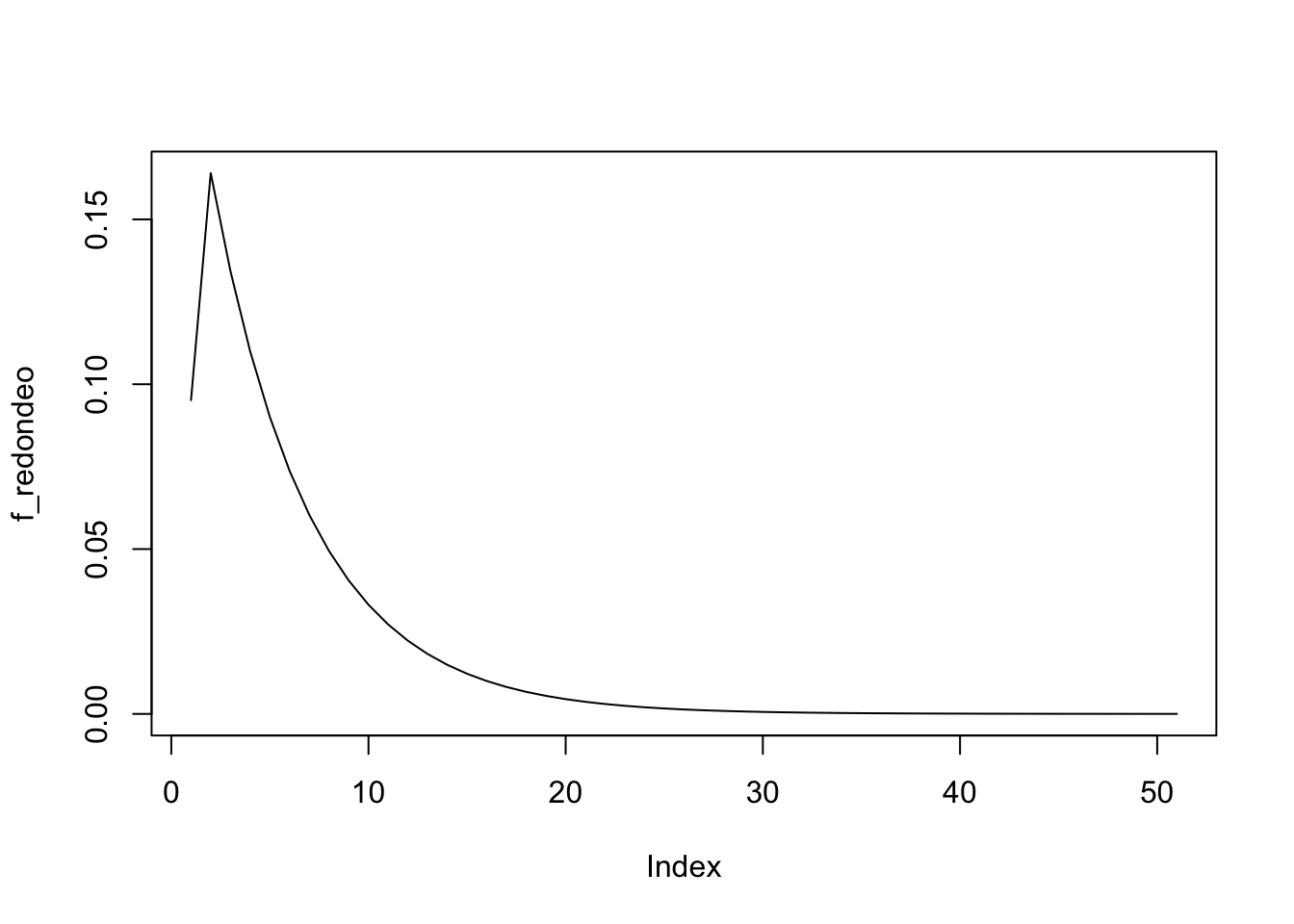
Para igualar el primer momento tenemos \(p=1\) y \(x_k=2 k\). Las ecuaciones clave se convierten en
\[\begin{equation*} \begin{array}{l} m_0^k=\int_{2 k}^{2 k+2} \frac{x-2 k-2}{-2}(0.1) e^{-0.1 x} d x=5 e^{-0.1(2 k+2)}-4 e^{-0.1(2 k)}, \\ m_1^k=\int_{2 k}^{2 k+2} \frac{x-2 k}{2}(0.1) e^{-0.1 x} d x=-6 e^{-0.1(2 k+2)}+5 e^{-0.1(2 k)} \end{array} \end{equation*}\] and then \[\begin{equation*} \begin{aligned} f_0 &=m_0^0=5 e^{-0.2}-4=0.09365 \\ f_j &=m_1^{j-1}+m_0^j=5 e^{-0.1(2 j-2)}-10 e^{-0.1(2 j)}+5 e^{-0.1(2 j+2)} \end{aligned} \end{equation*}\] Para este caso tome \(x_k=2k\) y \(p=1\)
Entonces \[\begin{align*} m_0^k & = 5e^{-0.1(2k+2)} -4e^{-0.1(2k)} \\ m_1^k & = -6e^{-0.1(2k+2)} +6e^{-0.1(2k)} \\ \end{align*}\]
m0k <- function(k) {
5 * exp(-0.1 * (2 * k + 2)) - 4 * exp(-0.1 * (2 * k))
}
m1k <- function(k) {
-6 * exp(-0.1 * (2 * k + 2)) + 5 * exp(-0.1 * (2 * k))
}
f_momentos <- m0k(0)
f_momentos[2:51] <- m1k(0:99) + m0k(1:50)Warning in f_momentos[2:51] <- m1k(0:99) + m0k(1:50): number of items to replace
is not a multiple of replacement lengthplot(f_momentos, type = "l")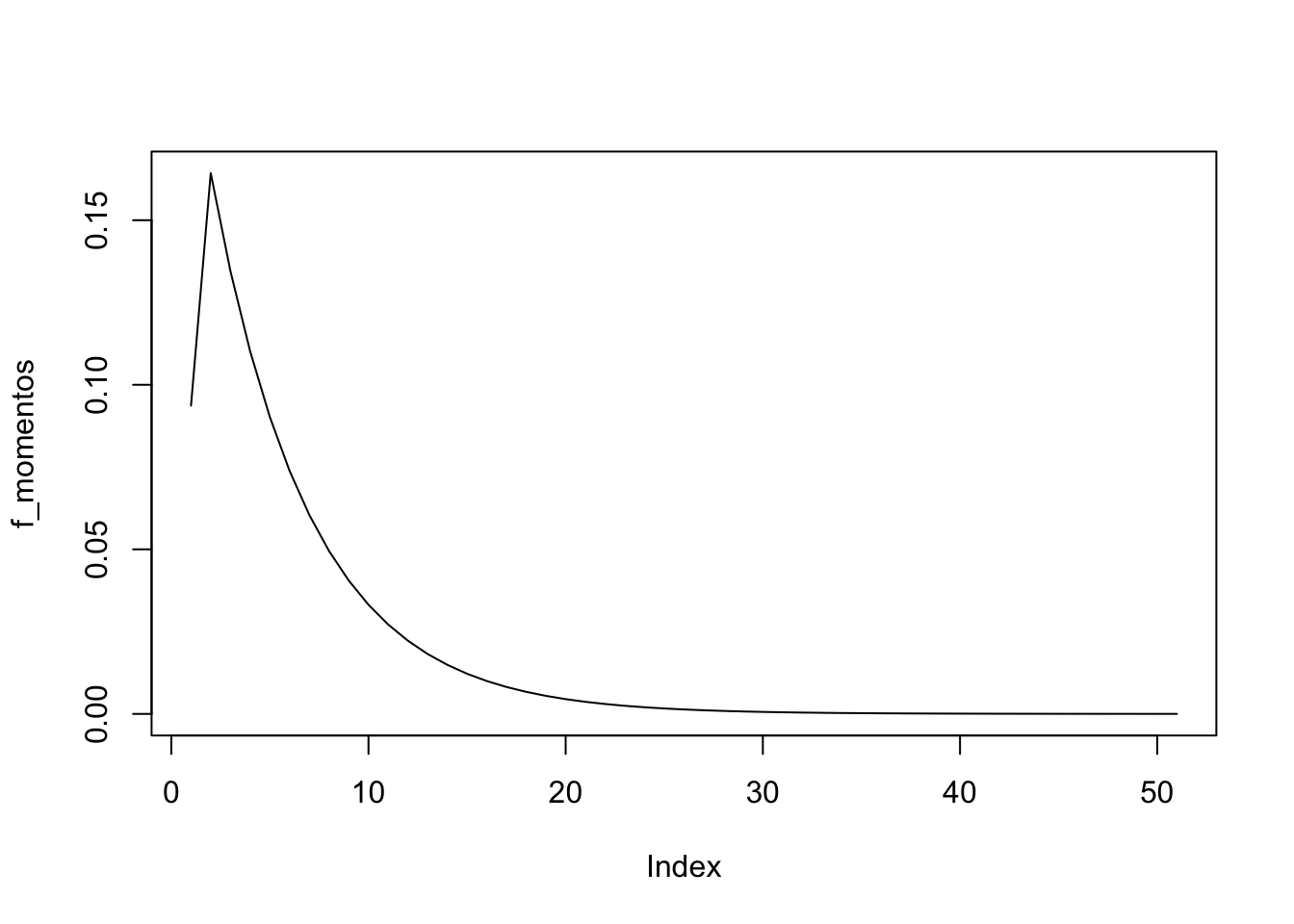
df_severidad_continua <- data.frame(k = 0:50, Redondeo = f_redondeo, Momentos = f_momentos) %>%
gather("tipo metodo", "densidad", -k)
ggplot(df_severidad_continua, aes(x = k, y = densidad, color = `tipo metodo`)) +
geom_line(size = 3) +
facet_wrap(~`tipo metodo`)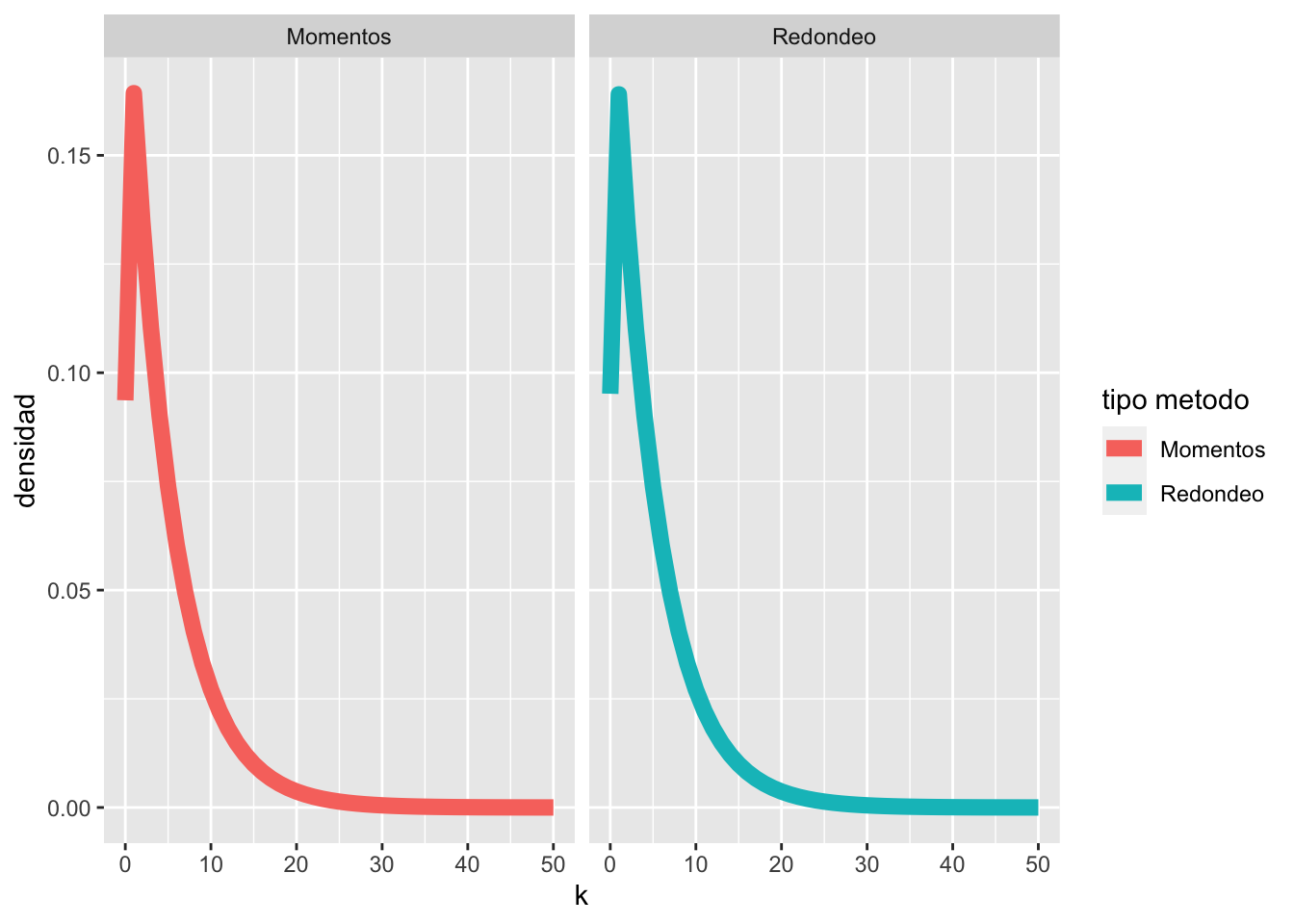
Para el caso de pérdidas agregadas lo que tenemos es para la variable de pérdidas \[\begin{equation*} S=Y_1^L+Y_2^L+\cdots+Y_{N^L}^L \end{equation*}\] con \(S=0\) si \(N^L=0\).
Además se puede construir la suma agregada de pagos como
\[\begin{equation*} S=Y_1^P+Y_2^P+\cdots+Y_{N^P}^P \end{equation*}\] con \(S=0\) si \(N^P=0\),
La función generadora de momentos para \(S\) se puede expresar para las pérdidas como \[\begin{equation*} M_S(z)=\mathrm{E}\left(e^{z S}\right)=P_{N^L}\left[M_{Y^L}(z)\right], \end{equation*}\] y para los pagos como \[\begin{equation*} M_S(z)=\mathrm{E}\left(e^{z S}\right)=P_{N^P}\left[M_{Y^P}(z)\right] \end{equation*}\]
De la misma forma que antes, \[\begin{equation*} P_{N^L}\left[M_{Y^L}(z)\right]=P_{N^L}\left[1-v+v M_{Y^P}(z)\right]=P_{N^P}\left[M_{Y^P}(z)\right] . \end{equation*}\]
Es decir, lo análisis para las pérdidas agregadas, se deben hacer usando las distribuciones compuestas respectivas.
El número de pérdidas de una compañía tiene una distribución de Poisson con media \(\lambda=3\). La distribución de pérdidas individuales es Pareto con parámetros \(\alpha=4\) y \(\theta=10\). Se aplica un deducible ordinario individual de 6 , un coaseguro de \(75 \%\), y un límite de pérdida individual de 24 (antes de la aplicación del deducible y coaseguro). Determine la media, la varianza y la distribución de los pagos agregados.
Solución. Primero calculamos la media y la varianza por pérdida. El número medio de pérdidas es \(\mathrm{E}\left(N^L\right)=3\), y el pago individual medio por pérdida es (usando el teorema \(8.7\) con \(r=0\) y la distribución de Pareto \()\)
\[\begin{equation*} \mathrm{E}\left(Y^L\right)=0.75[\mathrm{E}(X \wedge 24)-\mathrm{E}(X \wedge 6)]=0.75(3.2485-2.5195)=0.54675 \end{equation*}\] La media de los pagos agregados es entonces
\[\begin{equation*} \mathrm{E}(S)=\mathrm{E}\left(N^L\right) \mathrm{E}\left(Y^L\right)=(3)(0.54675)=1.64 \end{equation*}\] El segundo momento de los pagos individuales en una base por pérdida es, usando el Teorema 8.8 (página 128) del libro con \(r=0\) y la distribución de Pareto, \[\begin{equation*} \begin{aligned} \mathrm{E}\left[\left(X^L\right)^2\right]=&(0.75)^2\left\{\mathrm{E}\left[(X \wedge 24)^2\right]-\mathrm{E}\left[(X \wedge 6)^2\right]\right.\\ &-2(6) \mathrm{E}(X \wedge 24)+2(6) \mathrm{E}(X \wedge 6)\} \\ =&(0.75)^2[26.3790-10.5469-12(3.2485)+12(2.5195)] \\ =& 3.98481 \end{aligned} \end{equation*}\]
Para calcular la distribución (aproximada) de \(S\), usamos la base por pago. Primero tenga en cuenta que \(v=\operatorname{Pr}(X>6)=[10 /(10+6)]^4=0.15259\), y el número de pagos \(N^P\) tiene una distribución de Poisson con media \(\mathrm{E}\left(N^P\right)=\lambda v=3(0.15259)=0.45776\). Sea \(Z=X-6 \mid X>6\), de modo que \(Z\) es la variable aleatoria de pago individual con solo un deducible de 6 . Después \[\begin{equation*} \operatorname{Pr}(Z>z)=\frac{\operatorname{Pr}(X>z+6)}{\operatorname{Pr}(X>6)} . \end{equation*}\] Con coaseguro de \(75 \%, Y^P=0.75 Z\) tiene función de distribución acumulativa\[\begin{equation*} F_{Y_P}(y)=1-\operatorname{Pr}(0.75 Z>y)=1-\frac{\operatorname{Pr}(X>6+y / 0.75)}{\operatorname{Pr}(X>6)} . \end{equation*}\] Es decir, para \(y\) menos que el pago máximo de \((0.75)(24-6)=13.5\), \[\begin{equation*} F_{Y^P}(y)=\frac{\operatorname{Pr}(X>6)-\operatorname{Pr}(X>6+y / 0.75)}{\operatorname{Pr}(X>6)}, y<13.5 \end{equation*}\] y \(F_{Y_P}(y)=\) I para \(y \geq 13.5\). Luego, discretizamos la distribución de \(Y^l\) (por lo tanto, primero aplicamos las modificaciones de la política y luego discretizamos) usando un rango de \(2.25\) y el método de redondeo. Este enfoque produce \(f_0=F_{Y_P}(1.125)=0.30124, f_1=\) \(F_{Y^p}(3.375)-F_{Y^P}(1.125)=0.32768\), y así sucesivamente . En esta situación se debe tener cuidado en la evaluación de \(f_6\), y tenemos \(f_6=F_{Y^P}(14.625)-F_{Y^P}(12.375)=\) \(1- 0,94126=0,05874\). Entonces \(f_n=1-1=0\) para \(n=7,8, \ldots\).
La distribución aproximada de \(S\) se puede calcular usando la fórmula recursiva compuesta de Poisson, a saber, \(f_S(0)=e^{-0.45776(1-0.30124)}=0.72625\), y\[\begin{equation*} f_S(x)=\frac{0.45776}{x} \sum_{y=1}^{x \wedge 6} y f_y f_S(x-y), \quad x=1,2,3, \ldots \end{equation*}\]
Suponga que se tiene las mismas características del ejercicio anterior, pero con datos para N y X.
Con esto construya,
Este modelo asume que se tienen una suma fija de independientes (pero no necesariamente idénticamente distribuidas) variables aleatorias.
La suma correspondiente es \[\begin{equation*} S=X_1+X_2+\cdots+X_n. \end{equation*}\]
Es el caso de \(n\) personas diferentes, cubiertas bajo un grupo de polizas.
Para derivar el la distribución de pérdidas se tiene que para \(j-\)ésima póliza, suponga que se tiene la probabilidad de un evento \(q_j\) y un beneficio pagado en el evento \(j-\)ésimo de \(b_j\).
\[\begin{equation*} f_{X_{j}}(x)=\left\{\begin{array}{ll} 1-q_j, & x=0 \\ q_j, & x=b_j . \end{array}\right. \end{equation*}\]
La media y varianza son \[\begin{equation*} \mathrm{E}(S)=\sum_{j=1}^n b_j q_j \end{equation*}\] y \[\begin{equation*} \operatorname{Var}(S)=\sum_{j=1}^n b_j^2 q_j\left(1-q_j\right) \end{equation*}\]
como se supone que las \(X_j\) son independientes. Entonces, la pgf de las pérdidas agregadas es \[\begin{equation*} P_S(z)=\prod_{j=1}^n\left(1-q_j+q_j z^{b_j}\right) \end{equation*}\] En el caso especial donde todos los riesgos son idénticos con \(q_j=q\) y \(b_j=1\), el pgf se reduce a \[\begin{equation*} P_S(z)=[1+q(z-1)]^n . \end{equation*}\] y en este caso \(S\) tiene una distribución binomial.
Podemos generalizar este modelo definiendo \(X_j=I_j B_j\), con \(I_1 \ldots, I_n, B_1, \ldots, B_n\) son independientes.
La variable \(I_j\) se define como \[\begin{equation*} I_j = \begin{cases} 1 & \text{con probabilidad \(q_j\)} \\ 0 & \text{con probabilidad \(1-q_j\).} \end{cases} \end{equation*}\]
Mientras que \(B_j\) es una variable aleatoria (de cualquier distribución) que representa el \(j-\)ésimo pago. En el caso de un seguro de vida, se tiene que \(\mathbb{P}(B_{j}=b_{j})=1\).
La función generadora de momentos sería \[\begin{equation*} M_S(z)=\prod_{j=1}^n\left[1-q_j+q_j M_{B j}(z)\right] \end{equation*}\]
Si \(\mu_j=\mathrm{E}\left(B_j\right)\) y \(\sigma_j^2=\operatorname{Var}\left(B_j\right)\), entonces \[\begin{equation*} \mathrm{E}(S)=\sum_{j=1}^n q_j \mu_j \end{equation*}\] and \[\begin{equation*} \operatorname{Var}(S)=\sum_{j=1}^n\left[q_j \sigma_j^2+q_j\left(1-q_j\right) \mu_j^2\right] \end{equation*}\]
Para aproximar la distribución de \(S\) en el modelo de riesgo individual, se puede usar aproximaciones parametricas, o usar las mismas fórmulas de recursión del modelo colectivo en el individual.
Suponga que se tiene 14 empleados y cada uno de ellos es asegurado por el monto de su salario redondeado a los siguientes 1000 dólares. Para cada uno de ellos se tiene la siguiente información
tabla9.16 <- read.csv(text = "Empleado,Edad,Genero,Beneficio,Mortalidad
1,20,M ,15000,0.00149
2,23,M ,16000,0.00142
3,27,M ,20000,0.00128
4,30,M ,28000,0.00122
5,31,M ,31000,0.00123
6,46,M ,18000,0.00353
7,47,M ,26000,0.00394
8,49,M ,24000,0.00484
9,64,M ,60000,0.02182
10,17,F ,14000,0.0005
11,22,F ,17000,0.0005
12,26,F ,19000,0.00054
13,37,F ,30000,0.00103
14,55,F ,55000,0.00479
")
knitr::kable(tabla9.16)| Empleado | Edad | Genero | Beneficio | Mortalidad |
|---|---|---|---|---|
| 1 | 20 | M | 15000 | 0.00149 |
| 2 | 23 | M | 16000 | 0.00142 |
| 3 | 27 | M | 20000 | 0.00128 |
| 4 | 30 | M | 28000 | 0.00122 |
| 5 | 31 | M | 31000 | 0.00123 |
| 6 | 46 | M | 18000 | 0.00353 |
| 7 | 47 | M | 26000 | 0.00394 |
| 8 | 49 | M | 24000 | 0.00484 |
| 9 | 64 | M | 60000 | 0.02182 |
| 10 | 17 | F | 14000 | 0.00050 |
| 11 | 22 | F | 17000 | 0.00050 |
| 12 | 26 | F | 19000 | 0.00054 |
| 13 | 37 | F | 30000 | 0.00103 |
| 14 | 55 | F | 55000 | 0.00479 |
Si el patrono quisiera agregar un 45% extra a los costos del seguro, ¿Cuales son las probabilidades de que pierda dinero el próximo año?
La media está dada por \[\begin{equation*} \mathrm{E}(S)=\sum_{j=1}^{14} b_j q_j \end{equation*}\]
mu_S <- tabla9.16 %>%
mutate(prod = Beneficio * Mortalidad) %>%
summarise(sum(prod))
mu_S sum(prod)
1 2054.41La varianza
\[\begin{equation*} \operatorname{Var}(S)=\sum_{j=1}^{14} b_j^2 q_j\left(1-q_j\right) \end{equation*}\]
var_S <- tabla9.16 %>%
mutate(prod = Beneficio^2 * Mortalidad * (1 - Mortalidad)) %>%
summarise(sum(prod))
var_S sum(prod)
1 102533562Con la información anterior calcule la probabilidad que \(\mathbb{P}(S>\mu_S)\) asumiendo que la distribución de \(S\) es normal y lognormal. ¿Por qué hay una diferencia?
Ahora si uno desea usar la fórmulas recursivas, el truco se encuentra en cambiar el supuesto de que \(I_j\) es binomial con parámetros \(m=1\) y \(q=q_j\) a una Poisson con parámetro \(\lambda=q_j\). Otras aproximacioens para \(\lambda_j\) son \(-\log(1-q_j)\) o \(\frac{q_j}{1-q_j}\).
En todo caso,
\[\begin{equation*} M_S(z)=\prod_{j=1}^n \exp \left\{\lambda_j\left[M_{B_j}(z)-1\right]\right\}=\exp \left\{\lambda\left[M_X(z)-1\right]\right\} \end{equation*}\] con \[\begin{equation*} \begin{aligned} \lambda &=\sum_{j=1}^n \lambda_j \\ M_X(z) &=\lambda^{-1} \sum_{j=1}^n \lambda_j M_{B_j}(z) \end{aligned} \end{equation*}\] y \(X\) tiene distribución, \[\begin{equation*} f_X(x)=\lambda^{-1} \sum_{j=1}^n \lambda_j f_{B_j}(x) \end{equation*}\] la cual es un promedio ponderado de \(n\) severidades individuales.
Usando una aproximación Poisson, replique los valores de la tabla 9.17 del texto.
Para esto defina \(\lambda=\sum \lambda_{j} = \sum q_j\)