10 Análisis Exploratorio de Datos

Antes de comenzar con cualquier análisis estadístico, es fundamental realizar un análisis exploratorio de los datos (AED). Este proceso implica explorar y comprender los datos antes de aplicar cualquier técnica estadística o modelo. El AED es crucial para identificar errores, evaluar supuestos, seleccionar modelos y determinar las relaciones entre las variables.

Por qué debemos escuchar nuestros datos.

Comprobación de errores.
Revisión de patrones anómalos.
Revisar los supuestos de los datos.
Generar hipótesis del modelo.
Selección preliminar del modelo a usar.
Determinar las relaciones entre las distintas variables.

Primero recordemos que existen distintos de tipos de datos:

graph TD
    categoricos[Categóricos]
    cuantitativos[Cuantitativos]
    categoricos --> binarios[Binarios\nDos categorías]
    categoricos --> nominales[Nominales\n Más de dos categorías]
    categoricos --> ordinales[Ordinales\n El orden importa]
    cuantitativos --> discretos[Discretos\n Enteros]
    cuantitativos --> continuos[Continuos\n Reales]

Podemos clasificar el AED en dos categorías: No gráficos y los gráficos.

10.1 AED no gráfico

10.1.1 Tablas de frecuencia

En este tipo de arreglos es usado principalmente para variables categóricas o variables continuas con pocos valores distintos. En este contaremos las ocurrencias de cada una de las categorías de las variables y las ordenaremos en un arreglo rectangular. Además, podemos calcular la proporción o peso que representa cada una de las categorías con respecto al total.También se puede agregar los totales marginales de cada variable.

library(tidyverse)

data <-read_csv("data/edades.csv")
head(data)

# A tibble: 6 × 2
  genero  edad
  <chr>  <dbl>
1 F         21
2 F         35
3 F         40
4 F         30
5 F         25
6 F         39

Podemos crear los grupos de edad con la función cut y luego usar la función table para obtener la tabla de frecuencias.

data <- data |>
  mutate(grupo_edad = cut(edad, breaks = c(20, 42, 62, 82), labels = c("(21,42]", "(42,62]", "(62,82]")))
table(data$genero, data$grupo_edad)

   
    (21,42] (42,62] (62,82]
  F      13       9      10
  M       6       6      10

prop.table(table(data$genero, data$grupo_edad))

   
      (21,42]   (42,62]   (62,82]
  F 0.2407407 0.1666667 0.1851852
  M 0.1111111 0.1111111 0.1851852

10.1.2 Medidas de tendencia central

Asumamos que la serie de datos para una variable es $x_1,\ldots,x_n$.

Media empírica: Esta cantidad mide la tendencia central de los datos y se calcula de la siguiente forma \[\hat{\mu} = \bar{x} = \frac{1}{n} \sum_{i=1}^n x_i.\]

Esta pondera todos los datos en caso de tengan una ponderación igualitaria. Existen otros tipos de medias donde se puede dar más valor a ciertos datos dependiendo de ciertas características. Otra forma de
Mediana empírica: Esta es otra medida de tendencia central y se obtiene ordenando $x_1,\ldots,x_n$ y tomando justamente el valor que se encuentre en la mitad de la lista. El valor de la mediana dependerá del valor de $n$:
- Si $n$ es par: Entonces \[\hat{m} = \frac{x_{\frac{n}{2}} + x_{\frac{n}{2}+1}}{2}\]
- Si $n$ es impar: Entonces \[\hat{m} = x_{\frac{n+1}{2}}\]
  
  Si hubiera un numero par de datos, entonces se toma la media de los dos valores medios.
Moda: Esta medida casi no se usa; ya que, a veces no existe en los datos. El valor más frecuente de la serie de datos o “Picos que tiene la distribución”

En caso de distribuciones simétricas, la media y la mediana empíricas coinciden. Para datos asimétricos unimodales, la media se encuentra más cerca de la cola más larga.

La medida es robusta, es decir, cambiar unos cuantos valores no afecta el valor del estimado.

Código

# Cargar las librerías necesarias
library(ggplot2)
library(cowplot)
library(dplyr)

set.seed(123)

# Generar datos para la distribución simétrica (normal)
datos_normales <- rnorm(100, mean = 50, sd = 10)

# Generar datos para la distribución asimétrica (exponencial)
datos_exponenciales <- rexp(100, rate = 0.1) + 30

# Calcular media y mediana para la distribución normal
estadisticas_normales <- data.frame(
  Estadistica = c("Media", "Mediana"),
  Valor = c(mean(datos_normales), median(datos_normales))
)

# Calcular media y mediana para la distribución exponencial
estadisticas_exponenciales <- data.frame(
  Estadistica = c("Media", "Mediana"),
  Valor = c(mean(datos_exponenciales), median(datos_exponenciales))
)

# Crear histograma para la distribución normal
p1 <- ggplot() +
  geom_histogram(aes(x = datos_normales), binwidth = 5, fill = "skyblue",
                 color = "black") +
  geom_vline(data = estadisticas_normales,
             aes(xintercept = Valor, color = Estadistica), linetype = "dashed",
             linewidth = 2) +
  scale_color_manual(values = c("Media" = "red", "Mediana" = "blue")) +
  theme_minimal() +
  ggtitle("Distribución Simétrica") +
  labs(x = "", y = "") +
  theme(legend.position = "none") +
  cowplot::theme_cowplot()

# Crear histograma para la distribución exponencial
p2 <- ggplot() +
  geom_histogram(aes(x = datos_exponenciales), binwidth = 5, fill = "skyblue",
                 color = "black", ) +
  geom_vline(data = estadisticas_exponenciales,
             aes(xintercept = Valor, color = Estadistica), linetype = "dashed",
             linewidth = 2) +
  scale_color_manual(values = c("Media" = "red", "Mediana" = "blue")) +
  theme_minimal() +
  ggtitle("Distribución Asimétrica") +
  labs(x = "", y = "") +
  cowplot::theme_cowplot()

legend <- get_legend(
  # create some space to the left of the legend
  p1 + theme(legend.box.margin = margin(0, 0, 0, 12))
)

# Combinar los gráficos con cowplot para una comparación directa
plot_final <- plot_grid(
  p1 + theme(legend.position = "none"),
  p2 + theme(legend.position = "none"),
  labels = "AUTO"
)
plot_final <- plot_grid(plot_final, legend, ncol = 2, rel_widths = c(1, .2))
# Mostrar el gráfico combinado
print(plot_final)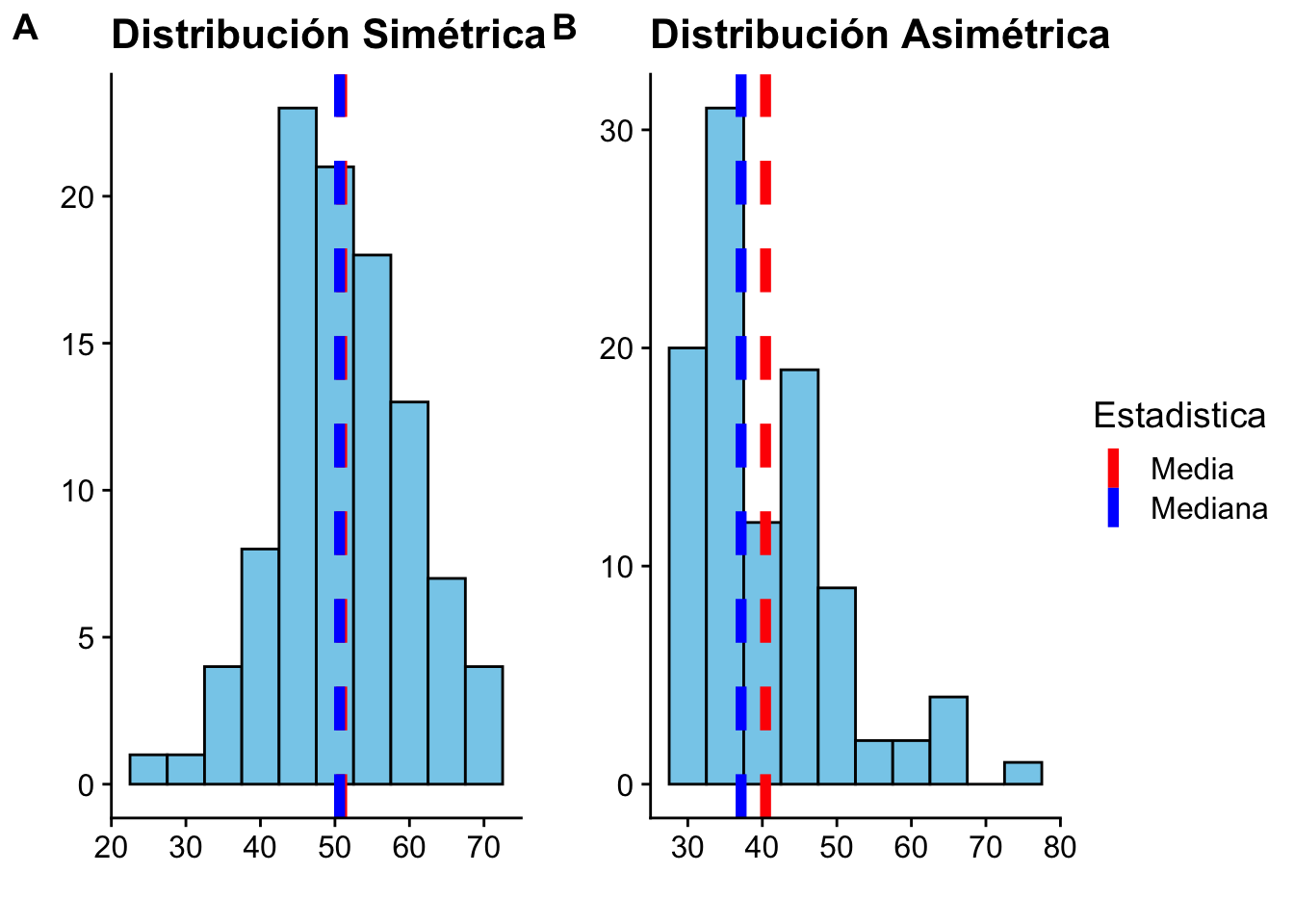

10.1.3 Medidas de desviación

Mide que tan lejos se encuentran los datos, los unos de los otros.

Varianza: Se obtiene promediando los errores al cuadrado de nuestros datos, mediante las siguientes ecuaciones:

\[\begin{equation*} \begin{aligned} \hat{\sigma}^2 & = \frac{1}{n} \sum_{i=1}^n {(X_i - \hat{\mu})}^{2}.\ \text{\bf{Sesgado}} \\ \hat{s}^2 & = \frac{1}{n-1} \sum_{i=1}^n {(X_i - \hat{\mu})}^{2}.\ \text{\bf{Insesgado}} \end{aligned} \end{equation*}\]

Desviación Estandar: Es la raíz cuadrada de la varianza. \[s = \sqrt{\hat{s}^2} = \sqrt{\frac{1}{n-1} \sum_{i=1}^n {(X_i - \hat{\mu})}^2.}\] El valor $s$ mide cuanto en promedio los datos se alejan de la media.
Rango interquantil: Un quantil de valor $\alpha$ es el valor que tal que: \[\mathbb{P}(X \leq q) = \alpha\] \[0<p<1\] \[q(\alpha)=F^{-1} (p)=\inf{x\colon F(x)\geq p}\] Definimos $Q_1 , Q_2 , Q_3$ de la siguiente forma: \[\mathbb{P}(X \leq Q_1)=0.25\] \[\mathbb{P}(X \leq Q_2)=0.5\] \[\mathbb{P}(X \leq Q_3)=0.75\]

La función fivenum genera los 5 números de Tukey que representan \[\{\min{X}, Q_1, Q_2, Q_3, \max{X}\}.\]

El IQR se define como: \[IQR=Q_3 - Q_1\]

Al igual que la mediana, el IQR es una medida robusta de esparcimiento. Para encontrar “outliers” en los datos se puede comparar el $Q_1$ y $Q_2$ con el minimo y máximo de los datos.

10.1.4 Medidas de Asimetría y curtosis

Asimetría: es el indicador que dice que tan ladeada está la distribución. La fórmula para la asimetría es: \[\begin{align*} \gamma_1 &= \mathbb{E}\left[\left(\frac{X-\mu}{\sigma}\right)^3\right] \\ &= \frac{\mu_3}{\sigma^3} \\ \end{align*}\]
Curtosis: es una medida de que tan alta es la distribucion se define con: \[\gamma=\frac{\mu_3}{(\mu_2 )^\frac{3}{2}}\] \[\begin{align*} \kappa &= \mathbb{E}\left[\left(\frac{X-\mu}{\sigma}\right)^4\right] \\ &= \frac{\mu_4}{\sigma^4} \\ \end{align*}\]

Sin embargo esta medida para distribuciones normales es 3. Por lo que para normalizarlo, se puede definir la curtosis de exceso como:

\[\begin{equation*} \gamma_2 = \frac{\mu_4}{\sigma_4}-3 = \kappa - 3. \end{equation*}\]

10.1.5 Covarianza y correlación

Teóricamente para dos v.a $X$, $Y$ se puede calcular el nivel de relación que existe entre estas. A esa medida se denomina Covarianza. Esta medida debe la escala de cada variable.

\[\begin{align*} \sigma_{xy} &= Cov(X,Y) = \mathbb{E}[(\mathbb{E}(X)-X)(\mathbb{E}(Y)-Y)] \\ &=\mathbb{E}(XY) - \mathbb{E}(X)\mathbb{E}(Y) \\ \hat{\sigma}_{xy}&= \frac{1}{n-1}\sum_{i=1}^n (X_i - \overline{X})(Y_i - \overline{Y}) \end{align*}\]

Ahora, se define la correlación como la covarianza estandarizada en el intervalo [-1,1], donde la relación positiva perfecta es 1, y la relación perfecta negativa -1.

\[\begin{align*} \rho &= Corr(X,Y)= \frac{Cov(X,Y)}{\sigma_x \sigma_y} \\ \hat{\rho} &= \frac{\sum_{i=1}^{n} (X_i - \overline{X})(Y_i - \overline{Y})}{\sqrt{\sum_{i=1}^{n} (X_i - \overline{X})^2}\sqrt{\sum_{i=1}^{n} (Y_i - \overline{Y})^2}} \\ \end{align*}\]

10.2 AED gráfico

10.2.1 Datos univariados

10.2.1.1 Histograma

Es una combinación de la tabla de contingencias y los diagramas de tallo y hoja pero para cualquier tipo de variable. Este gráfico proporciona el conteo o a totalidad de los datos:

Seleccionar un origen $x_0$ y defina los intervalos

\[B_j =(x_0 + (j-1)h,x_0 +jh)\quad j\in\mathbb{Z} \quad h>0\]
Cuento cuantas observaciones caen en cada intervalo $B_j$, llame ese numero $n_j$.
Divida cada $n_j$ entre el total de observaciones $n$ y defina:

\[f_j = \frac{n_j}{n} \]
Para cada uno de los intervalos, $B_i$, dibuje una barra de altura $f_i$ y ancho h.

Finalmente definimos el histograma como función $dx$. $F$ es la densidad verdadera (desconocida) de $x$

\[\hat{F_n}(x)= \frac{1}{nh}\sum_{i=1}^n\sum_{j}I(X_i\in B_j)I(x\in B_j) \\ (X_i\in B_j)=\left\{ \begin{array}{l l} 1 & \quad \text{Si $X_i \in B_j$}\\ 0 & \quad \text{Otro caso} \end{array} \right.\]

El ancho de la caja afecta la presentación de los datos; ya que, pueden mostrar distribuciones muy planas o muy picadas. El histograma es un estimador no parammetrico de la densidad.

# Generar datos de ejemplo
set.seed(123)
datos <- rnorm(1000, mean = 50, sd = 10)

# Definir origen y ancho del intervalo
# Un poco menor que el mínimo valor para incluir todos los datos
x0 <- min(datos) - 0.5
# Ancho de intervalo elegido
h <- 5

# Crear el histograma ggplot2 ajusta automáticamente los intervalos, pero para
# este ejemplo, definiremos el ancho de bin manualmente
ggplot(data.frame(datos), aes(x = datos)) +
  geom_histogram(
    binwidth = h, color = "black",
    fill = "skyblue", boundary = x0
  ) +
  xlab("Valor") +
  ylab("Frecuencia relativa") +
  ggtitle("Histograma con Ancho de Intervalo Definido") +
  cowplot::theme_cowplot()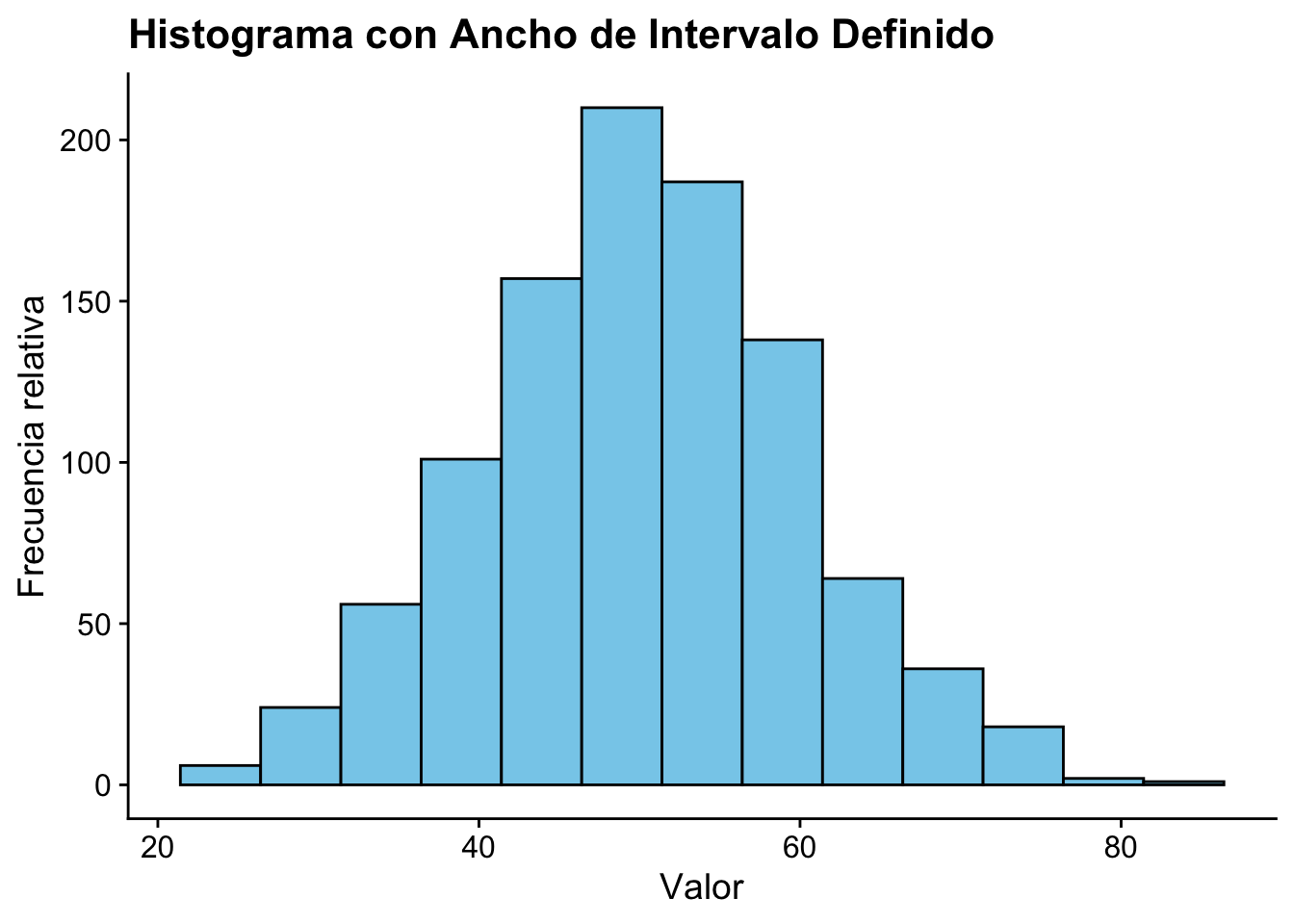

10.2.2 Gráficos de caja (Boxplot)

Son gráficos que resumen casi de inmediato elementos de la distribución de una muestra como el IQR, la mediana, la asimetría y los outlers.
Estos no logran percibir la multimodalidad.

datos <- c(-3.2, -1.7, -0.4, 0.2, 0.3, 1.2,
           1.5, 1.8, 2.4, 3.0, 4.3, 6.8, 9.0)
ggplot() +
  geom_boxplot(aes(y = datos))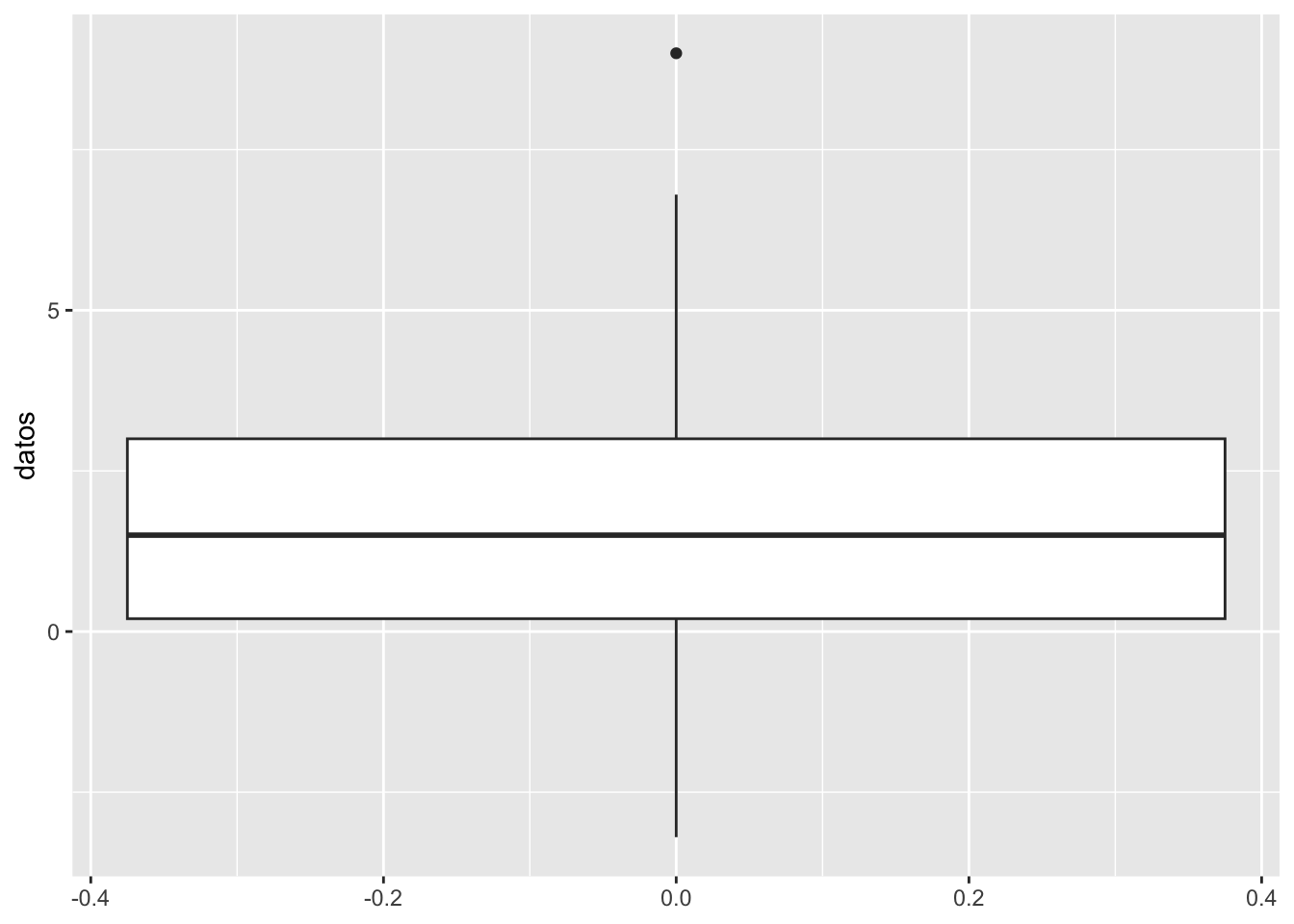

Código

datos <- c(-3.2, -1.7, -0.4, 0.2, 0.3, 1.2, 1.5, 1.8, 2.4, 3.0, 4.3, 6.8, 9.0)


Q1 <- quantile(datos, 0.25)
Q3 <- quantile(datos, 0.75)
mediana <- median(datos)
limite_inferior_lim <- Q1 - 1.5 * IQR(datos)
limite_superior_lim <- Q3 + 1.5 * IQR(datos)

limite_superior <- max(datos[datos <= limite_superior_lim])
limite_inferior <- min(datos[datos >= limite_inferior_lim])

# Identificar outliers
outliers <- datos[datos < limite_inferior | datos > limite_superior]
size_label <- 5
# Crear el boxplot con anotaciones y flechas
ggplot(mapping = aes(y = datos)) +
  geom_boxplot(color = "blue") +
  ggtitle("Boxplot Anotado con Flechas") +
  ylab("Valor") +
  xlab("") +
  theme_minimal() +
  geom_label(aes(
    x = 0.7,
    y = Q3,
    label = paste("Q3 =", round(Q3, 2))
  ), hjust = 0, nudge_x = 0, size = size_label, label.size = NA) +
  geom_label(aes(
    x = 0.7,
    y = Q1,
    label = paste("Q1 =", round(Q1, 2))
  ), hjust = 0, nudge_x = 0, size = size_label, label.size = NA) +
  geom_label(aes(
    x = 0.7,
    y = mediana,
    label = paste("Mediana =", round(mediana, 2))
  ), hjust = 0, nudge_x = 0, size = size_label, label.size = NA) +
  geom_label(aes(
    x = 0.7,
    y = limite_superior,
    label = paste("Bigote sup. =", round(limite_superior, 2))
  ),
  hjust = 0,
  nudge_x = 0,
  color = "red",
  size = size_label,
  label.size = NA) +
  geom_label(aes(
    x = 0.7,
    y = limite_inferior,
    label = paste("Bigote inf. =", round(limite_inferior, 2))
  ),
  hjust = 0,
  nudge_x = 0,
  color = "red",
  size = size_label,
  label.size = NA) +
  geom_label(
    aes(
      x = 0.7,
      y = outliers[1],
      label = paste("Outliers =", round(outliers[1], 2))
    ),
    color = "red",
    hjust = 0,
    size = size_label,
    label.size = NA
  ) +
  geom_segment(aes(
    x = 0.7,
    y = Q3,
    xend = 0.4,
    yend = Q3
  ), arrow = arrow(type = "closed", length = unit(0.2, "inches")),
  color = "red") +
  geom_segment(aes(
    x = 0.7,
    y = Q1,
    xend = 0.4,
    yend = Q1
  ), arrow = arrow(type = "closed", length = unit(0.2, "inches")),
color = "red") +
  geom_segment(aes(
    x = 0.7,
    y = mediana,
    xend = 0.4,
    yend = mediana
  ),
 arrow = arrow(type = "closed", length = unit(0.2, "inches")), color = "red") +
  geom_segment(
    aes(
      x = 0.7,
      y = limite_superior,
      xend = 0.05,
      yend = limite_superior
    ),
    arrow = arrow(type = "closed", length = unit(0.2, "inches")),
    color = "red"
  ) +
  geom_segment(aes(
    x = 0.7,
    y = limite_inferior,
    xend = 0.05,
    yend = limite_inferior
  ), arrow = arrow(type = "closed", length = unit(0.2, "inches")),
color = "red") +
  geom_segment(aes(
    x = 0.7,
    y = outliers[1],
    xend = 0.05,
    yend = outliers[1]
  ), arrow = arrow(type = "closed", length = unit(0.2, "inches")),
color = "red") +
  coord_cartesian(xlim = c(-0.5, 1)) +
  cowplot::theme_nothing()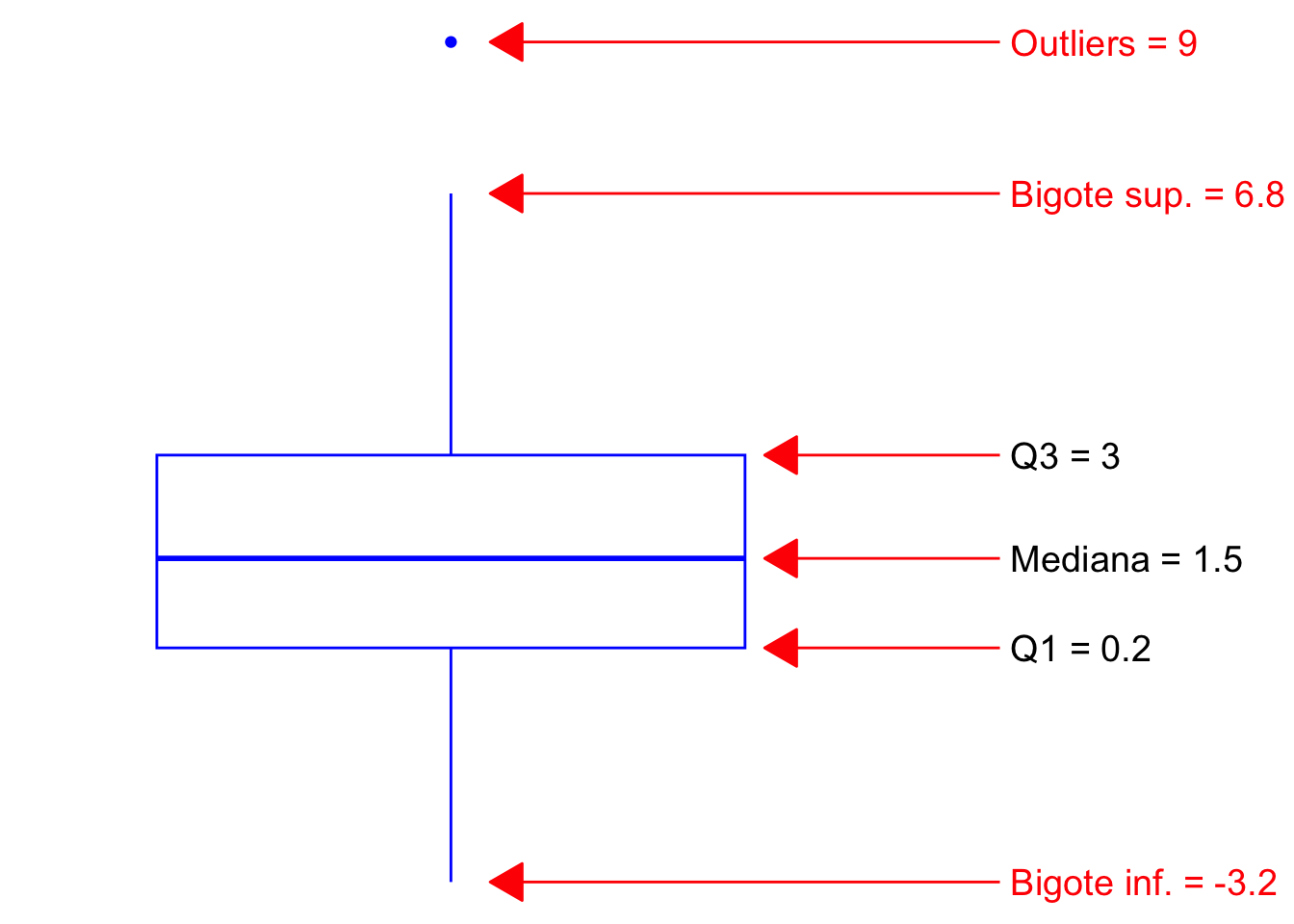

Tukey definió que un punto extremo es aquel que estuvieron fuera del rango: \[(Q_1 - 1.5 \times IQR, Q_3 + 1.5 \times IQR)\]

Esta regla fue basada en la distribución normal donde alrededor 1 de 100 puntos se declararían como extremos

Observación. ¿Que pasaría si la regla fuera 2 IQR?

Entonces en el ejemplo

\[\begin{align*} Q_3 + 1.5\times IQR &= 3 + 1.5 \times 2.8 = 7.2 \\ Q_1 -1.5\times IQR &= 3 -1.5 \times 2.8 = -4 \end{align*}\]

Entonces el bigote superior sería al valor máximo que sea menor a 7.2 y el bigote inferior sería el valor mínimo que sea mayor a -4. En este caso serían 6.8 y -3.2 respectivamente.

10.2.3 QQ-plots

Los quantile-quantile (QQ) plots son herramientas gráficas utilizadas para evaluar si una muestra sigue una distribución teórica específica. Comúnmente, se emplean para comparar si una muestra se ajusta a una distribución gaussiana (normal).

Nota Importante: Un QQ-plot no se limita solo a dibujar pares ordenados de datos de la muestra contra valores teóricos esperados bajo una distribución específica. Esta técnica es fundamental en estadística ya que muchos modelos, como los de regresión, asumen normalidad en los residuos. Es crucial verificar este supuesto para validar adecuadamente un modelo estadístico.

Lo primero es seleccionar los cuantiles muestrales tal y como lo explicamos anteriormente. Es decir, cuál es el punto de corte de modo que podamos acumular cierta probabilidad.

Los puntos teóricos se pueden seleccionar de la siguiente manera: \[p_i = \frac{i - \frac{1}{2}}{n}\] O alternativamente, usando: \[p_{i,\alpha,\beta} = \frac{i-\alpha}{n+1-\alpha-\beta}\] Donde $\alpha, \beta \in \mathbb{R}$.

Según Hyndman (1996), es crucial analizar el comportamiento de $p_{i,\alpha,\beta}$ para distintos valores de $\alpha$ y $\beta$. En este estudio, se demuestra que establecer $\alpha=\beta=\frac{1}{2}$ cumple con varias propiedades deseables para la estimación de cuantiles. Por otro lado, Blom (1958) sugiere que $\alpha=\beta=\frac{3}{8}$ ofrece un mejor ajuste para distribuciones normales, aunque no satisface todas las condiciones ideales.

Para datos que se aproximan a una distribución normal, se utiliza la fórmula: \[p_i=\frac{i-\frac{3}{8}}{n-\frac{1}{4}}\]

Ahora, el objetivo es comparar los datos con otra distribución teórica. Para ello, se usa la recta $y = x$ como referencia. La lógica detrás es simple: si los puntos de nuestra muestra se alinean cercanamente a la recta $y = x$, entonces se puede inferir que los datos siguen la distribución teórica.

Ejemplo 10.1 Siguiendo con el ejemplo anterior, se muestra cómo realizar un QQ-plot en con las funciones base de R con un conjunto de datos y compararlos con una distribución normal teórica:

datos <- c(-3.2, -1.7, -0.4, 0.2, 0.3, 1.2, 1.5, 1.8, 2.4, 3.0, 4.3, 6.8, 9.0)

qqnorm(datos, col = "blue", pch = 19)
qqline(datos, col = "red")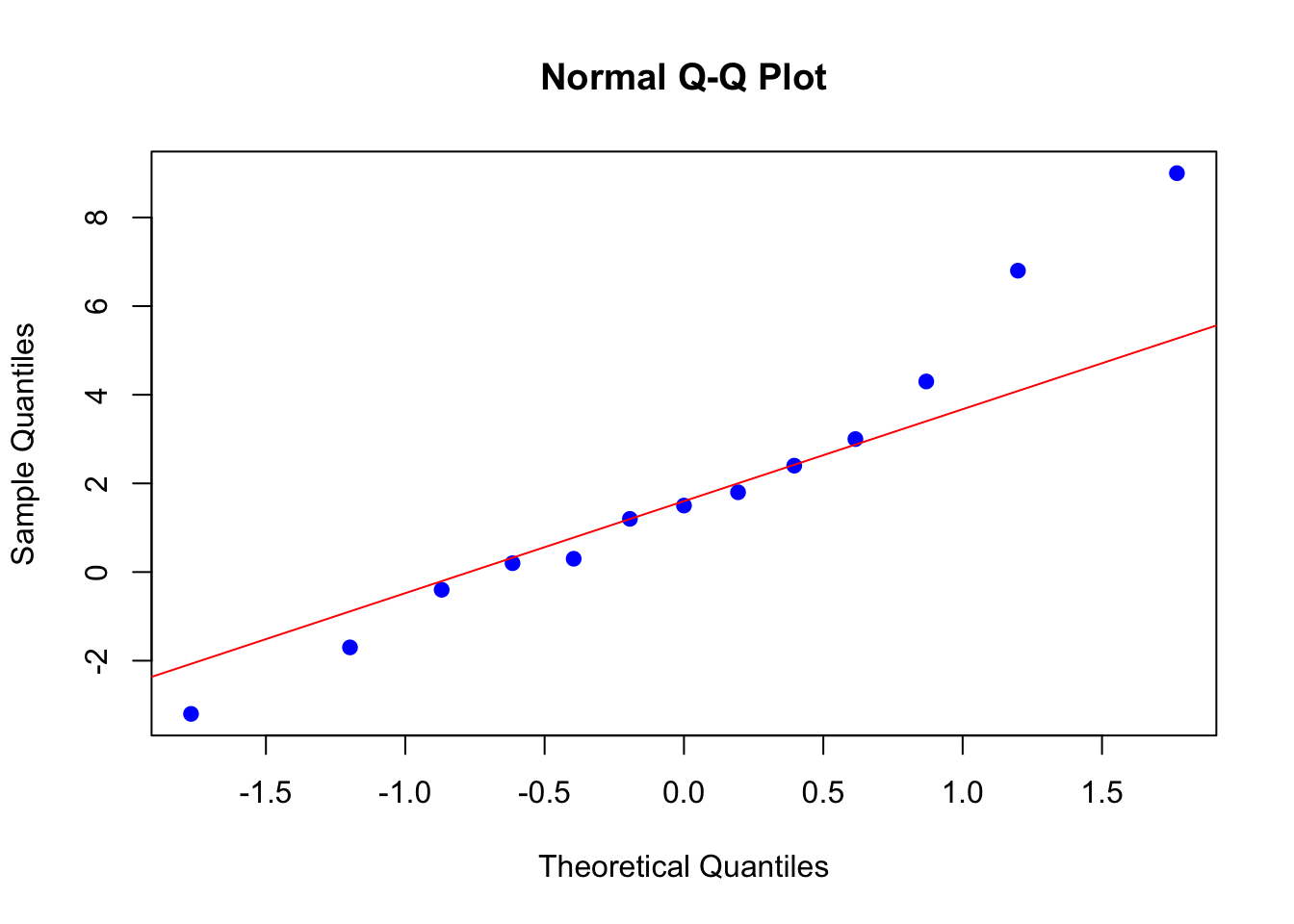

Si lo queremos hacer en ggplot2, podemos usar la función geom_qq:

df <- data.frame(y = datos)
ggplot(df, aes(sample = y)) +
  geom_qq(color = "blue") +
  geom_qq_line(color = "red") +
  cowplot::theme_cowplot()

Ejemplo 10.2 A continuación, se muestra cómo realizar un QQ-plot en R con un conjunto de datos lognormales y compararlos con una distribución normal teórica:

set.seed(123)
datos_lognormales <- rlnorm(100, meanlog = 0, sdlog = 1)

qqnorm(datos_lognormales, col = "blue", pch = 19)
qqline(datos_lognormales, col = "red")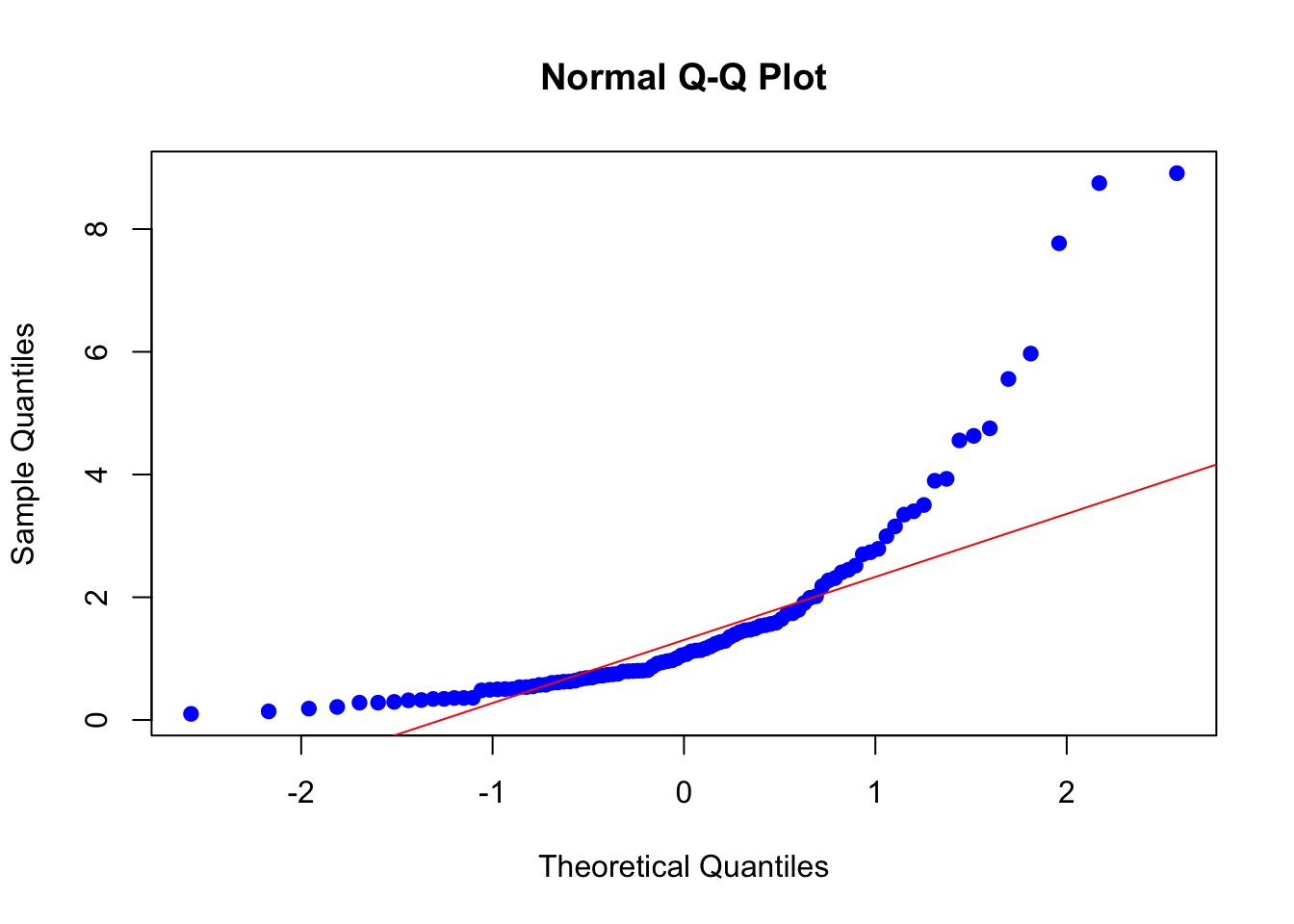

set.seed(123)
datos_normales <- rnorm(100, mean = 0, sd = 1)

qqnorm(datos_normales, col = "blue", pch = 19)
qqline(datos_normales, col = "red")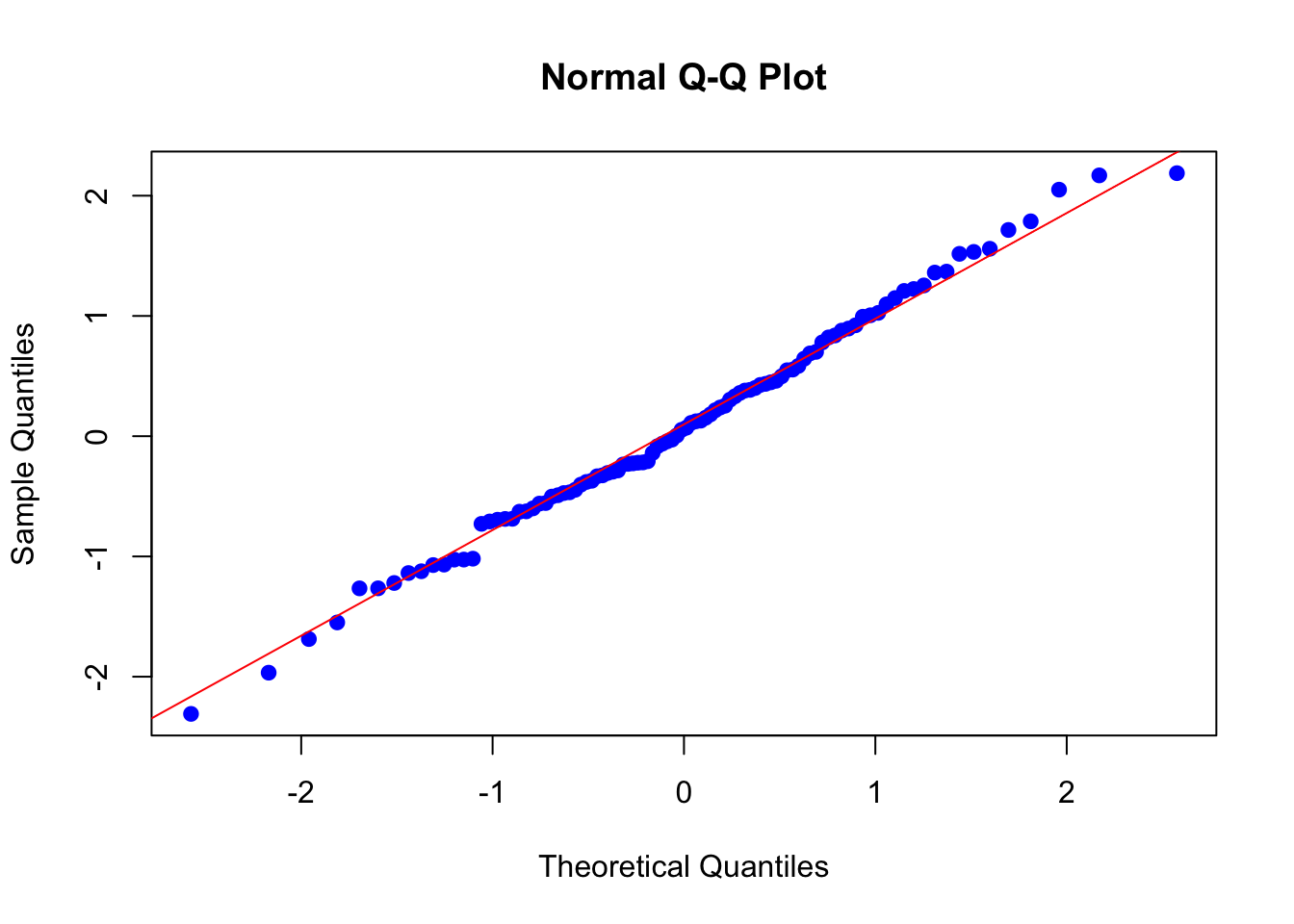

10.2.4 Datos bivariados

Para los datos bivariados podemos usar la siguiente tabla de referencia

Variable 1	Variable 2	Tipo de gráfico
Categórica	Categórica	Barras (stacked)
Categórica	Continua	Boxplot
Continua	Continua	Puntos / Líneas

10.2.4.1 Gráficos de Barras

Los gráficos de barras son esenciales para comparar cantidades entre categorías distintas. Aquí algunos puntos clave y buenas prácticas para su creación:

Representación de Categorías: Cada barra representa una categoría diferente, haciendo fácil la comparación visual entre ellas.
Longitud Proporcional: La longitud de cada barra es proporcional a la magnitud que representa, facilitando la comparación de valores.
Ancho Uniforme: Las barras deben tener el mismo ancho para evitar distorsiones visuales.
Espaciado Uniforme: Mantener una distancia igual entre las barras mejora la claridad.
Base Cero: Iniciar el eje de valores en cero asegura una representación fiel de las magnitudes. Hay que tener cuidado en este punto ya que en ocasiones se puede perder información relevante.
Evitar Margenes: Los márgenes en las barras pueden complicar la interpretación visual de los datos.
Etiquetas Claras: Asegúrate de que las categorías y valores sean fáciles de leer y entender.

Hay que tener

Ejemplo 10.3

# Datos de ejemplo
datos <- data.frame(
  Categoria = c("A", "B", "C", "D"),
  Valor = c(23, 45, 10, 30)
)

ggplot(datos, aes(x = Categoria, y = Valor)) +
  geom_bar(stat = "identity", fill = "skyblue", color = "black") +
  theme_minimal() +
  labs(title = "Gráfico de Barras", x = "Categoría", y = "Valor")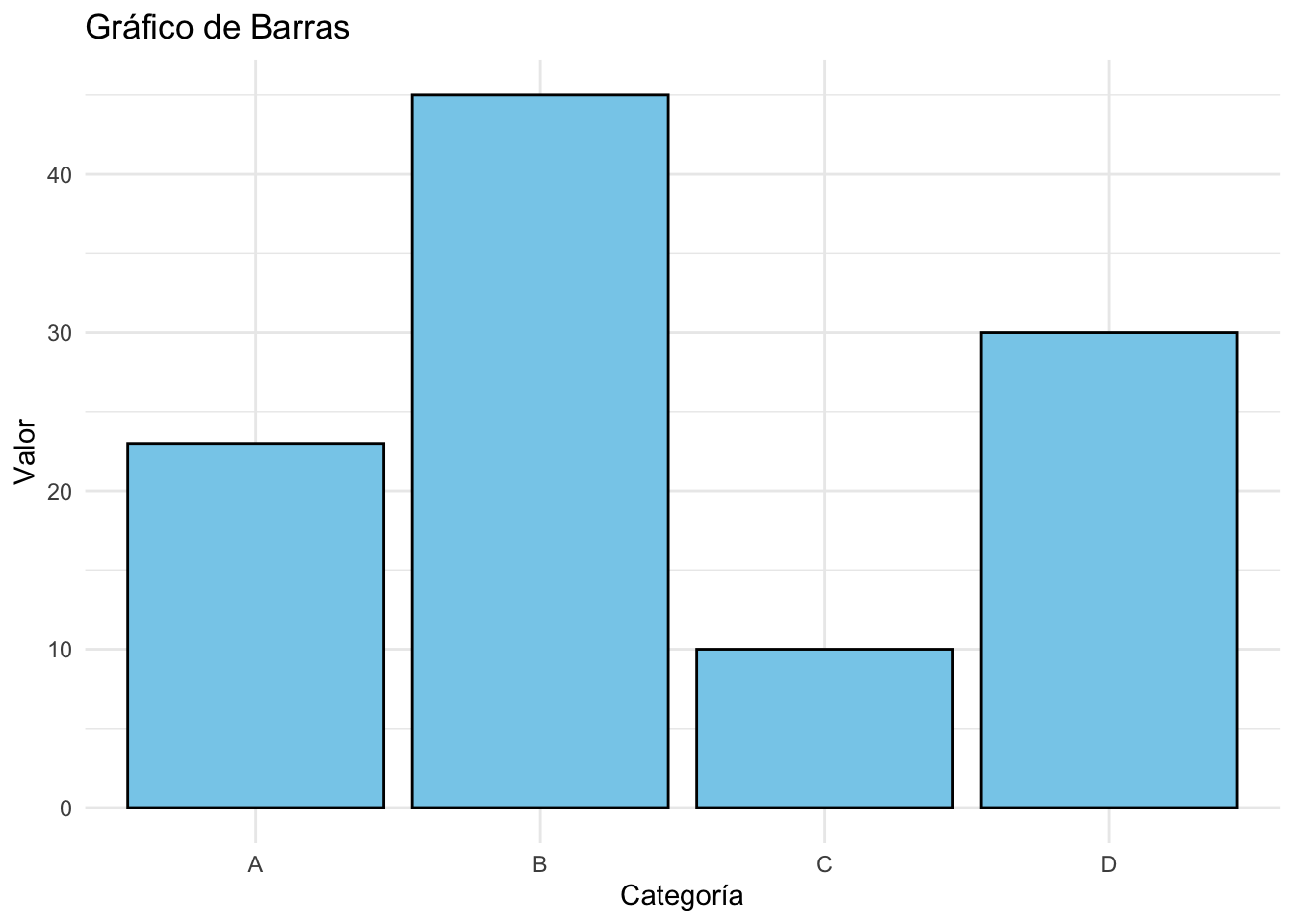

10.2.4.2 Gráficos de Líneas

Los gráficos de líneas son una herramienta fundamental en la visualización de datos, especialmente útiles para mostrar tendencias o cambios a lo largo del tiempo. Este tipo de gráfico conecta puntos de datos individuales con líneas, lo que facilita la percepción de la dirección y el ritmo de cambio en los datos.

Se debe considerar lo siguiente:

Escala Temporal: El eje X representa el tiempo, con puntos igualmente espaciados.
Variables Continuas: Adecuados para cualquier par de variables cuantitativas donde una es continua.
Proporcionalidad: El eje Y debe reflejar la magnitud real de los datos, preferentemente iniciando en cero para evitar distorsiones visuales.
Base Cero: Mantener el eje Y comenzando en cero, a menos que se quieran destacar pequeñas variaciones.
Diferenciación: Usar colores y estilos de línea distintos para múltiples series de datos.
Claridad: Evitar el exceso de series en un solo gráfico para mantener la interpretación sencilla.
Leyendas y Anotaciones: Proporcionar contexto con leyendas claras y anotaciones cuando sea necesario.

Ejemplo 10.4

ventas <- data.frame(
  Mes = factor(1:12, labels = month.abb),
  Ventas = c(120, 150, 130, 170, 160, 180, 200, 220, 210, 230, 240, 260)
)

# Gráfico de líneas
ggplot(ventas, aes(x = Mes, y = Ventas, group = 1)) +
  geom_line(color = "blue", linewidth = 1) + # Línea azul
  geom_point(color = "red", size = 2) + # Puntos rojos
  theme_minimal() +
  scale_y_continuous(limits = c(0, 300)) + # Manteniendo la base cero
  labs(title = "Ventas Mensuales a lo Largo del Año",
       x = "Mes", y = "Ventas ($)") +
  theme(legend.position = "none") # Sin leyenda en este caso simple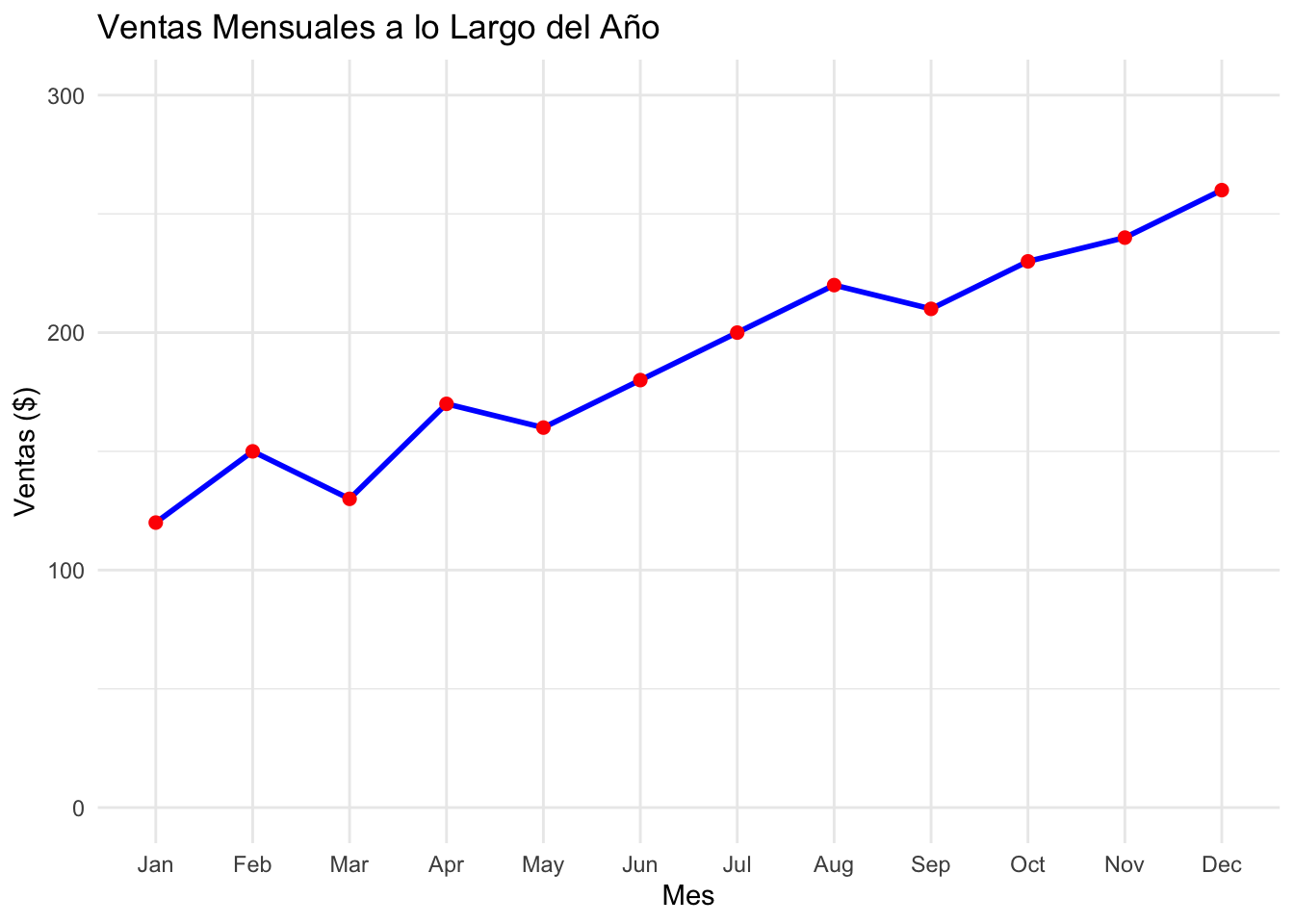

10.2.4.3 Gráfico de Dispersión (Scatterplot)

Los gráficos de dispersión son esenciales en estadística para explorar la relación entre dos variables cuantitativas, permitiendo identificar patrones, tendencias y posibles correlaciones.

Variables Cuantitativas: Los gráficos de dispersión son ideales para comparar dos variables cuantitativas, donde cada punto representa un par de valores.
Correlación: Una de las principales utilidades de los gráficos de dispersión es evaluar la presencia y dirección de una correlación entre las variables.
Identificación de Outliers: Permiten identificar valores atípicos que podrían influir en el análisis.
Escala Adecuada: Asegúrate de que ambos ejes reflejen adecuadamente el rango de datos para cada variable, evitando distorsiones.
Marcadores Diferenciados: Si el gráfico incluye categorías (datos agrupados), utiliza colores o formas de marcadores diferentes para distinguir entre grupos.
Evitar Sobrecarga: Demasiados puntos sobre una pequeña área pueden hacer que el gráfico sea difícil de leer. Considera usar transparencia o jittering si es necesario.
Análisis Complementario: A menudo, los gráficos de dispersión revelan la necesidad de análisis estadísticos adicionales, como ajustes de línea o modelos de regresión.

set.seed(42)
x <- rnorm(100)
y <- x + rnorm(100, mean = 0.1)
datos <- data.frame(
  x = x,
  y = y,
  Categoria = as.factor(sample(c("Grupo 1", "Grupo 2"), 100, replace = TRUE))
)

ggplot(datos, aes(x = x, y = y, color = Categoria)) +
  geom_point(size = 3) +
  labs(title = "Gráfico de Dispersión con Categorías") +
  scale_color_manual(values = c("Grupo 1" = "blue", "Grupo 2" = "red")) +
  cowplot::theme_cowplot()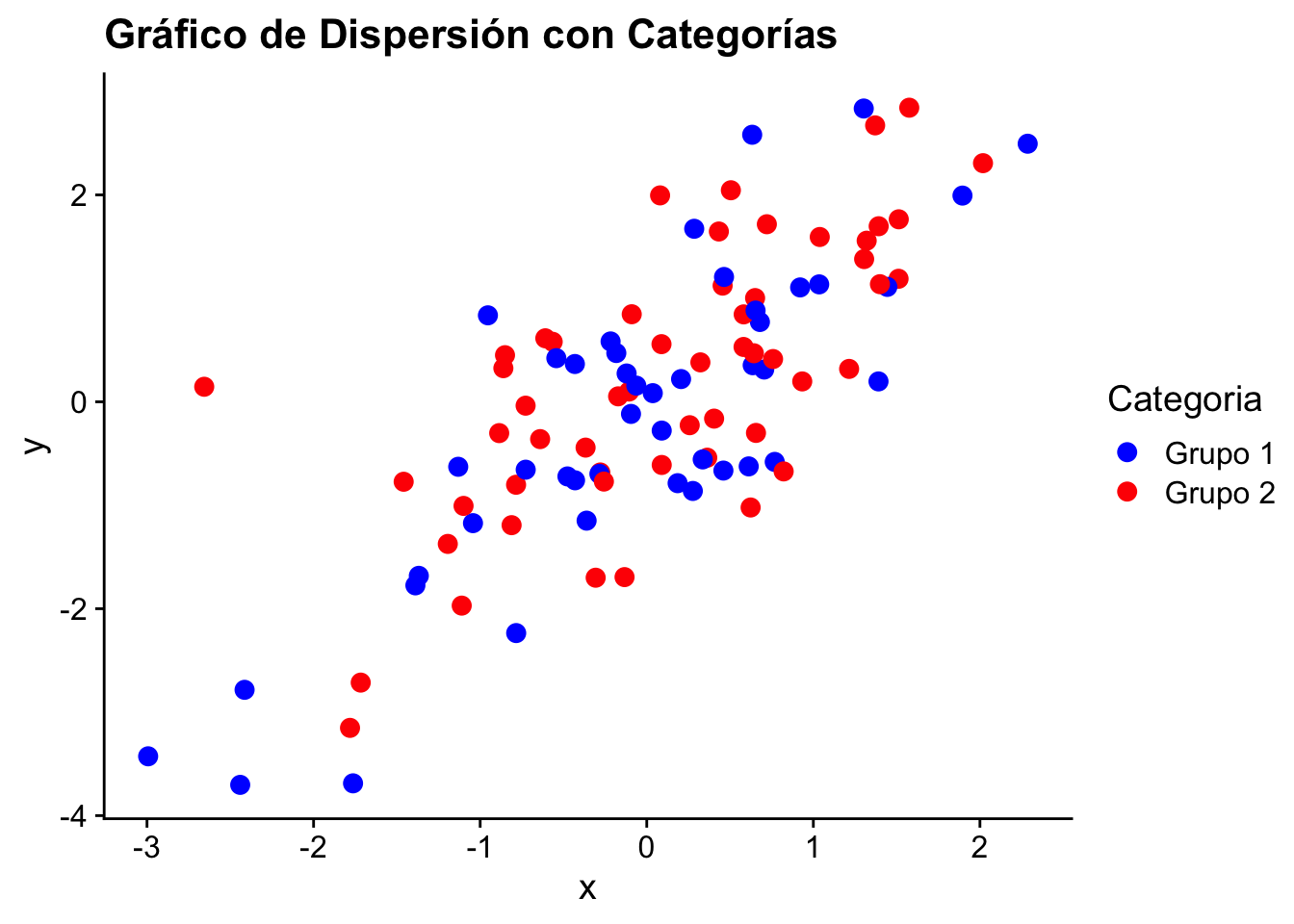

10.2.4.4 Gráficos pastel

Advertencia

Nunca use gráficos de pastel. Los gráficos de barras son superiores en casi todos los aspectos. Los gráficos de barras son más fáciles de leer, menos engañosos y menos susceptibles a la manipulación.

Código

# Libraries
library(tidyverse)
library(hrbrthemes)
library(viridis)
library(patchwork)

# create 3 data frame:
data1 <- data.frame( name=letters[1:5], value=c(17,18,20,22,24) )
data2 <- data.frame( name=letters[1:5], value=c(20,18,21,20,20) )
data3 <- data.frame( name=letters[1:5], value=c(24,23,21,19,18) )

# Plot
plot_pie <- function(data, vec){

ggplot(data, aes(x="name", y=value, fill=name)) +
  geom_bar(width = 1, stat = "identity") +
  coord_polar("y", start=0, direction = -1) +
  scale_fill_viridis(discrete = TRUE,  direction=-1) +
  geom_text(aes(y = vec, label = rev(name), size=4, color=c( "white", rep("black", 4)))) +
  scale_color_manual(values=c("black", "white")) +
  theme_ipsum() +
  theme(
    legend.position="none",
    plot.title = element_text(size=14),
    panel.grid = element_blank(),
    axis.text = element_blank(),
    legend.margin=unit(0, "null")
  ) +
  xlab("") +
  ylab("")

}

a <- plot_pie(data1, c(10,35,55,75,93))

Warning: `legend.margin` must be specified using `margin()`
ℹ For the old behavior use `legend.spacing`

b <- plot_pie(data2, c(10,35,53,75,93))

Warning: `legend.margin` must be specified using `margin()`
ℹ For the old behavior use `legend.spacing`

c <- plot_pie(data3, c(10,29,50,75,93))

Warning: `legend.margin` must be specified using `margin()`
ℹ For the old behavior use `legend.spacing`

a + b + c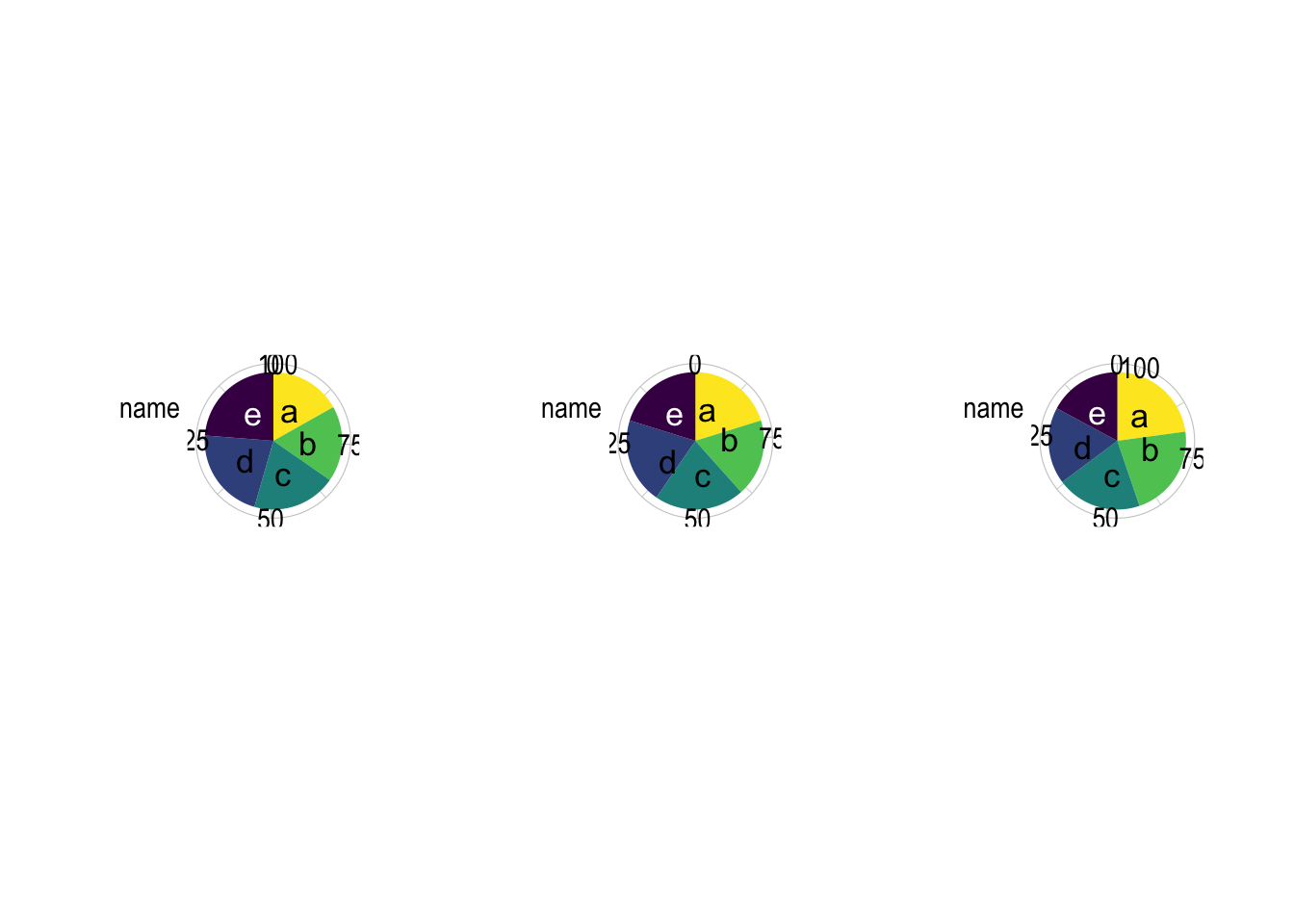

Ejercicio 10.1 Revisar este sitio https://www.data-to-viz.com/caveats.html y comentar cuales son los ejemplos que más le llamaron la atención.