4 Densidades previas conjugadas y estimadores de Bayes
4.1 Distribución previa (distribución a priori)
Cuando trabajamos con un modelo estadístico con un parámetro desconocido \(\theta\), es común en el enfoque bayesiano considerar a \(\theta\) como una variable aleatoria. La distribución que describe nuestras creencias o conocimientos previos sobre \(\theta\) antes de observar cualquier dato se llama densidad previa y se denota por \(\pi(\theta)\).
Observación. La función de distribución previa \(\pi\) tiene las siguientes características.
- Está definida en \(\Omega\) (espacio paramétrico).
- Se establece antes de obtener cualquier muestra.
Hagamos algunos ejemplos para entender como funciona la densidad previa.
Ejemplo 4.1 (Componentes eléctricos) Consideremos el tiempo de vida de ciertos componentes que sigue una distribución exponencial \(X_1,\dots, X_n \sim \text{Exp}(\theta)\). Si suponemos que \(\theta\) es una variable aleatoria que sigue una distribución Gamma con parámetros \(\alpha = 1\) y \(\beta = 2\), entonces la densidad previa de \(\theta\) es:
\[\begin{equation*} \pi(\theta) = \dfrac{1}{\Gamma(\alpha)}\beta^\alpha\theta^{\alpha-1}e^{\beta\theta} = 2e^{2\theta}, \quad \theta > 0 \end{equation*}\]
Ejemplo 4.2 (Lanzamiento de una moneda) Supongamos que estamos interesados en averiguar la probabilidad de obtener cara al lanzar una moneda, en un experimento donde hay dos tipos de monedas: las monedas justas y las monedas alteradas. Sin embargo, hay incertidumbre sobre qué moneda se va a utilizar en la siguiente lanzada, podría ser una moneda justa o una moneda alterada que siempre cae en cara, pero se sabe que su densidad previa sigue una distribución Gamma, por lo que antes de observar cualquier lanzamiento, modelamos nuestras creencias sobre \(\theta\), asumiendo la densidad previa calculada en el ejercicio anterior, de la siguiente manera:
- Moneda justa: La probabilidad de que \(\theta = \dfrac{1}{2}\) es \(0.8\), i.e. , \(\pi(\frac{1}{2}) = 0.8\)
- Moneda alterada: La probabilidad de que \(\theta = 1\) es \(0.2\), i.e. , \(\pi(1) = 0.2\).
Esto significa que si tuviéramos 100 monedas, esperaríamos que 20 de ellas fueran alterada y 80 fueran justas.
Ejemplo 4.3 (Componentes eléctricos (cont.)) Supongamos que estamos interesados en el tiempo de vida de un componente eléctrico. Sabemos que este tiempo se puede modelar con una distribución exponencial con parámetro \(\theta\). Además, basándonos en la experiencia de un experto, creemos que \(\theta\) tiene una distribución previa Gamma. El experto nos proporciona la siguiente información:
\[ \mathbb{E}[\theta] = 0.0002, \quad \sqrt{\text{Var}(\theta)} = 0.0001 \]
Dada la distribución Gamma, sus momentos están definidos en función de sus parámetros \(\alpha\) (forma) y \(\beta\) (tasa). Específicamente, para una variable aleatoria $ $ que sigue una distribución Gamma, sus momentos están dados por:
\[\begin{align*} \mathbb{E}[\theta] &= \frac{\alpha}{\beta} = 0.0002 \\ \text{Var}(\theta) &= \frac{\alpha}{\beta^2} = 0.0001^2 \end{align*}\]
Por lo tanto despejando \(\alpha\) y \(\beta\) tenemos que:
\[\begin{align*} \beta &= \frac{\alpha}{0.0002} \\ \alpha &= 0.0001^2 \beta^2 \end{align*}\]
Sustituyendo en ambas ecuaciones, obtenemos que:
\[\begin{align*} \alpha &= 4 \\ \beta &= 20000. \end{align*}\]
Ejemplo 4.4 (Continuación de Ejemplo 4.3) Considerando el contexto del componente eléctrico discutido anteriormente, si tomamos una muestra \(X = (X_1, \dots, X_n)\) donde cada \(X_i\) sigue una distribución exponencial con parámetro \(\theta\) y \(X_i > 0\), la función de densidad conjunta condicionada en \(\theta\) se describe como:
\[\begin{align*} f_n(X|\theta) &= \prod_{i=1}^n \theta e^{-\theta X_i} \\ &= \theta^n e^{-\theta\sum_{i=1}^n X_i}. \end{align*}\]
4.2 Densidad posterior
Una vez que observamos los datos, actualizamos nuestras creencias sobre \(\theta\) usando el teorema de Bayes. La distribución resultante se llama densidad posterior y se denota por \(\pi(\theta|X)\).
Teorema 4.1 Dada una muestra aleatoria compuesta por las observaciones \(X_1, X_2, \dots, X_n\), podemos definir la densidad posterior de \(\theta\) como:
\[ \pi(\theta|X) = \frac{f(X_1|\theta) f(X_2|\theta) \dots f(X_n|\theta) \pi(\theta)}{g_n(X)} \]
Aquí, \(g_n(X)\) actúa como una constante de normalización que asegura que la densidad posterior integre a uno.
Prueba. Para derivar la expresión anterior, aplicamos directamente el Teorema de Bayes. La fórmula de Bayes nos dice que:
\[ \pi(\theta|X) = \frac{\pi(X|\theta) \pi(\theta)}{\pi(X)} \]
Expandiendo la densidad conjunta y reorganizando términos, obtenemos:
\[ \pi(\theta|X) = \frac{f_n(X|\theta) \pi(\theta)}{\int \pi(\theta,X) \, d\theta} \]
Esto se simplifica a:
\[ \pi(\theta|X) = \frac{f(X_1|\theta) f(X_2|\theta) \dots \times f(X_n|\theta) \times \pi(\theta)}{g_n(X)} \]
Esta expresión nos da la densidad posterior de \(\theta\) dada la muestra observada.
Ejemplo 4.5 (Componentes eléctricos (cont.)) Supongamos que tenemos una muestra \(X = (X_1, X_2, \dots, X_n)\) donde cada observación \(X_i\) sigue una distribución exponencial. La función de verosimilitud para esta muestra está dada por:
\[ f_n(X|\theta) = \theta^n e^{-\theta y}. \]
Aquí, \(y = \sum_{i=1}^n X_i\) representa la suma total de las observaciones y actúa como un estadístico para \(\theta\).
Para calcular la densidad posterior de \(\theta\), necesitamos considerar tanto la función de verosimilitud como la densidad previa. Desglosemos esto en dos partes: el numerador y el denominador de la densidad posterior \(\pi(\theta\vert X)\):
- Numerador: El numerador se compone de la función de verosimilitud y la densidad previa:
\[\begin{equation*} f_n(X|\theta)\pi(\theta) = \underbrace{\theta^n e^{-\theta y}}_{f_n(X|\theta)} \cdot \underbrace{\dfrac{20000^4}{3!}\theta^3e^{-20000\cdot\theta}}_{\pi(\theta)} = \dfrac{20000^4}{3!}\theta^{n+3}e^{-(20000+y)\theta} \end{equation*}\]
- Denominador: El denominador es una constante de normalización que asegura que la densidad posterior integre a uno1:
\[\begin{equation*} g_n(x) = \int_{0}^{+\infty}\theta^{n+3}e^{-(20000+y)\theta}\;d\theta = \dfrac{\Gamma(n+4)}{(20000+y)^{n+4}}. \end{equation*}\]
Con estos componentes, la densidad posterior de \(\theta\) es:
\[ \pi(\theta|X) = \frac{\theta^{n+3}e^{-(20000+y)\theta}}{\Gamma(n+4)}(20000+y)^{n+4} \]
Esta densidad posterior sigue una distribución \(\Gamma(n+4, 20000+y)\).
Supongamos que observamos 5 tiempos de fallo: 2911, 3403, 3237, 3509, y 3118. Entonces, \(y = 16478\) y \(n = 5\). Con estos datos, la distribución posterior de \(\theta\) es \(\Gamma(9, 36178)\).
La distribución posterior es sensible al tamaño de la muestra. Es decir, que una muestra grande inicial, implica un efecto menor de la previa.
Observación. Le decimos Hiperparámetros a los parámetros de la previa o posterior.
4.3 Proceso de modelación de parámetros
De ahora en adelante vamos a entender un modelo como la unión de los siguientes componentes:
- El conjunto de los datos \(X_1, \ldots, X_n\),
- La función de densidad \(f\)
- El parámetro de la densidad \(\theta\).
Estos dos últimos resumen el comportamiento de los datos.
Para identificar y trabajar con este modelo, lo desglosamos en las siguientes partes:
- Información previa (\(\pi(\theta)\)): Esta es la información adicional o basada en la experiencia que tenemos sobre el modelo.
- Verosimilitud: Los datos representan la información observada. La función de densidad \(f\) refina y mejora la información previa. La función \(f_n(X|\theta)\) se conoce como verosimilitud o función de verosimilitud y se define como: \[ f_n(X|\theta) = \prod_{i=1}^n f(X_i|\theta). \]
- Densidad posterior: Es una combinación de la información previa y los datos observados, proporcionando una versión más informada de la distribución del parámetro. Se calcula como: \[ \pi(\theta|X) \propto f_n(x|\theta)\pi(\theta). \]
- Predicciones con datos nuevos: Si asumimos que los datos se obtienen secuencialmente, podemos calcular la distribución posterior de la siguiente manera: \[\begin{align*} \pi(\theta|X_1) & \propto \pi(\theta) f(X_1|\theta)\\ \pi(\theta|X_1,X_2) &\propto \pi(\theta) f(X_1,X_2|\theta) \\ & = \pi(\theta) f(X_1|\theta) f(X_2|\theta) \text{ (por independencia condicional)}\\ & = \pi(\theta|X_1)f(X_2|\theta)\\ \vdots & \\ \pi(\theta|X_1,\dots,X_n) & \propto f(X_n|\theta)\pi(\theta|X_1,\dots, X_{n-1}) \end{align*}\] Bajo la suposición de independencia condicional, no hay diferencia en la posterior si los datos se obtienen secuencialmente. Esta distribución nos ayuda a calcular probabilidades sobre datos nuevos. Por lo tanto: \[\begin{align*} g_n(X) & = \int_{\Omega} f(X_n|\theta) \pi(\theta|X_1,\dots, X_{n-1})\;d\theta\\ & = P(X_n|X_1,\dots,X_{n-1}) \text{ (Predicción para }X_n) \end{align*}\]
Observación. En el caso de una función de verosimilitud, el argumento es \(\theta\) y los datos en \(X\) son fijos.
Ejemplo 4.6 (Proporción de componentes defectuosos) En ejemplos anteriores, abordamos los tiempos de vida de componentes defectuosos asumiendo un valor fijo para \(\theta\). Ahora, exploraremos cómo modelar este parámetro utilizando estadística bayesiana.
Consideremos un componente que puede ser defectuoso o no. Es natural modelar su comportamiento con una variable aleatoria \(X_i\) definida como:
\[\begin{equation*} X_i = \begin{cases} 0 & \text{falló} \\ 1 & \text{no falló} \end{cases} \end{equation*}\]
Donde \(\theta\) representa la proporción de componentes defectuosos, con \(\theta \in [0,1]\). Una elección adecuada para modelar esta variable aleatoria es asumir que \(X_i \sim \mathrm{Bernoulli}(\theta)\).
Siguiendo los pasos anteriores, definamos
Distribución Previa (\(\pi(\theta)\)): Sin información previa sobre los componentes, asumimos que \(\theta\) sigue una distribución uniforme en el intervalo \([0,1]\): \[ \pi(\theta) = 1_{\{0\leq\theta\leq 1\}} \] Es importante notar que una distribución uniforme es equivalente a una distribución \(\mathrm{Beta}(1,1)\).
Función de Verosimilitud: Esta función representa la probabilidad de observar nuestros datos dados ciertos valores de \(\theta\): \[ f_n(X|\theta) = \theta^{\sum_{i=1}^{n} X_i}(1-\theta)^{n-\sum_{i=1}^{n} X_i} = \theta^{y}(1-\theta)^{n-y} \] Donde \(y = \sum_{i=1}^{n} X_i\) es el número total de componentes que no fallaron.
Distribución Posterior: Combinando nuestra información previa (distribución previa) con la función de verosimilitud, obtenemos la distribución posterior de \(\theta\): \[ \pi(\theta|X) \propto \theta^y (1-\theta)^{n-y} = \theta^{y+1-1}(1-\theta)^{n-y+1-1} \] De esta expresión, deducimos que, dada la información \(X\), \(\theta\) sigue una distribución \(\text{Beta}(y+1,n-y+1)\).
Observación. La distribución posterior anteriormente es exactamente
\[\begin{equation*} \pi(\theta|X) = \frac{\Gamma(n+1)}{\Gamma(y+1)\Gamma(n-y+1)}\theta^{y}(1-\theta)^{n-y}. \end{equation*}\]
Sin embargo el operador \(\propto\) indica que el lado izquierdo es igual al lado derecho salvo por una constante que no depende de la variable (\(\theta\)). Esto es muy útil para evitar escribir mucho en las fórmulas.
Ejemplo 4.7 (Componentes eléctricos (cont.)) En el ejemplo Ejemplo 4.5, discutimos la modelación del tiempo de vida de componentes. Ahora supongamos que se nos presenta un nuevo dato, \(X_6\). Estamos interesados en determinar la probabilidad de que este nuevo componente tenga un tiempo de vida superior a 3000, es decir, \(P(X_6>3000|X_1,X_2,X_3,X_4,X_5)\).
Para calcular esta probabilidad, necesitamos determinar la función de densidad condicional \(f(X_6|X)\). Dado que la distribución posterior de \(\theta\) está dada por:
\[\begin{align*} \pi(\theta|X) &= \frac{36178^9}{\Gamma(9)} \theta^8 e^{-36178\theta} \\ &= 2.633\times 10^{36}\theta^8 e^{-36178\theta} \end{align*}\]
Podemos expresar la función de densidad condicional como:
\[\begin{align*} f(X_6|X) &= \int_{0}^\infty f(X_6|\theta) \pi(\theta|X)\;d\theta \\ &= \int_{0}^\infty \theta e^{-\theta X_6} \pi(\theta|X)\;d\theta \\ &= 2.633\times 10^{36} \int_{0}^\infty \theta e^{-\theta X_6} \theta^8 e^{-36178\theta}\;d\theta \\ &= 2.633\times 10^{36} \int_{0}^\infty \theta^9 e^{-\theta (X_6+36178)} \;d\theta \\ &= 2.633\times 10^{36} \dfrac{9!}{(X_6+36178)^{10}} \\ &= \dfrac{9.55 \times 10^{41}}{(X_6+36178)^{10}} \end{align*}\]
Con esta función en mano, podemos calcular la probabilidad deseada:
\[ P(X_6>3000\mid X) = \int_{3000}^{\infty} \dfrac{9.55\times10^{41}}{(X_6+36178)^{10}}\; dX_6 = 0.4882 \]
Observación. La vida media del componente se define como el tiempo en el cual la probabilidad de que el componente falle es del 50%. Matemáticamente, esto se expresa como:
\[ \dfrac{1}{2} = P(X_6>u|X) \]
En este caso, lo que tendríamos es que \[\begin{align*} \dfrac{1}{2} &= \int_{u}^{\infty} \dfrac{9.55\times10^{41}}{(X_6+36178)^{10}}\; dX_6 \\ &= \dfrac{ 9.55\times10^{41}}{-9(X_6+36178)^{9}}\Big|_{u}^{\infty} \\ &= \dfrac{ 9.55\times10^{41}}{9(u+36178)^{9}} \\ \end{align*}\]
Despejando tenemos que \[\begin{align*} \dfrac{1}{2} &= \dfrac{ 9.55\times10^{41}}{9(u+36178)^{9}} \\ (u + 36178)^9 &= \dfrac{ 9.55\times10^{41}}{9\cdot 0.5} \\ u + 36178 &= \sqrt[9]{\dfrac{ 9.55\times10^{41}}{9\cdot 0.5}} \\ u &= \sqrt[9]{\dfrac{ 9.55\times10^{41}}{9\cdot 0.5}} - 36178 \\ u &= 2894 \end{align*}\]
4.4 Familias conjugadas
En estadística bayesiana, las familias conjugadas desempeñan un papel fundamental al simplificar el proceso de actualización de nuestras creencias a medida que se obtienen nuevos datos. A continuación, se presenta una introducción detallada a este concepto.
Dada una muestra \(X_1, \dots, X_n\) que es independiente e idénticamente distribuida (i.i.d.) condicionalmente dado un parámetro \(\theta\) con densidad \(f(x\mid \theta)\), consideremos,\(\psi\) como la familia de posibles densidades previas sobre \(\Omega\).
Definición 4.1 Si, independientemente de los datos observados, la densidad posterior pertenece a la misma familia que \(\psi\), entonces decimos que \(\psi\) es una familia conjugada de previas.
Ejemplo 4.8
Para el Ejemplo Ejemplo 4.3, la familia Gamma es una familia conjugada para muestras exponenciales.
En el Ejemplo Ejemplo 4.6, la familia Beta es una familia conjugada para muestras según una Binomial.
Para el caso de datos que siguen una distribución Poisson, si \(X_1,\dots,X_n\sim\mathrm{Poisson}(\lambda)\),la familia Gamma es conjugada. La función de densidad de una Poisson es: \[\begin{equation*} P(X_i = k) = e^{-\lambda}\dfrac{\lambda^k}{k!} \end{equation*}\] La verosimilitud, que es el producto de las densidades de los datos observados, se da por: \[\begin{equation*} f_n(X|\lambda) = \prod_{i=1}^{n}e^{-\lambda}\dfrac{\lambda^{X_i}}{X_i!} = \dfrac{e^{-n\lambda}\lambda^{y}}{\prod_{i=1}^n X_i}. \end{equation*}\] Si la previa de \(\lambda\) está definida por \(\pi(\lambda)\propto\lambda^{\alpha-1}e^{-\beta\lambda}\), entonces la posterior es: \[\begin{equation*} \pi(\lambda|X) \propto \lambda^{y+\alpha-1}e^{-(\beta+n)\lambda} \implies \lambda|X \sim \Gamma(y+\alpha,\beta+n) \end{equation*}\]
En el caso de datos que siguen una distribución normal, \(X_1,\dots,X_n\sim N(\theta,\sigma^2)\), la familia normal es conjugada si la varianza \(\sigma^2\) es conocida. Si \(\theta \sim N(\mu_0,V_0^2)\) entonces la posterior para \(\theta\) data la muestra es \(\sim N(\mu_1, V_1^2)\) donde, \[\begin{align*} \mu_1 &= \dfrac{\sigma^2\mu_0 + nV_0^2 \bar X_n}{\sigma^2 + nV_0^2} = \dfrac{\sigma^2}{\sigma^2 + nV_0^2}\mu_0 + \dfrac{nV_0^2}{\sigma^2 + nV_0^2}\bar X_n\\ V_1^2 &= \frac{\sigma^2 V_0^2}{\sigma^2+n V_0^2}. \end{align*}\] Este resultado nos muestra cómo la información previa (representada por \(\mu_0\) y \(V_0^2\)) se combina con la información de la muestra (representada por \(\bar{X}_n\)) para producir una estimación posterior de \(\theta\).
En resumen, la tabla a continuación muestra algunas de las familias conjugadas más comunes en estadística bayesiana.
| Distribución | Previa conjugada |
|---|---|
| \(\text{Bernoulli}(p)\) | \(p \sim Beta(\alpha,\beta)\) |
| \(\text{Binomial}(n,p)\) | \(p \sim Beta(\alpha,\beta)\) |
| \(\text{Binomial Negativa}(n,p)\) | \(p \sim Beta(\alpha,\beta)\) |
| \(\text{Poisson}(\lambda)\) | \(\lambda \sim Gamma(\alpha,\beta)\) |
| \(\text{Exponencial}(\theta)\) | \(\theta \sim Gamma(\alpha,\beta)\) |
| \(\text{Normal}(\mu,\sigma^2)\) | \(\mu \sim N(\mu_0,\sigma^{2}_{0}) \quad \text{ y } \quad \sigma^{2} \sim GammaInversa(\alpha,\beta)\) |
Ejemplo 4.9 Considere un conjunto de datos que sigue una distribución \(\mathrm{Poisson}(\lambda)\). Supongamos que nuestra creencia previa sobre \(\lambda\) está dada por:
\[\begin{equation*} \pi(\lambda) = \begin{cases}2e^{-2\lambda} & \lambda> 0 \\ 0 & \lambda \geq 0\end{cases} . \end{equation*}\]
Esta previa de \(\lambda\) sigue una distribución \(\Gamma(1,2)\).
Si tenemos una muestra aleatoria de tamaño \(n\), nos interesa determinar cuántas observaciones necesitamos para que la varianza de nuestra estimación de \(\lambda\) sea, a lo sumo, 0.01.
Para abordar esta pregunta, primero definimos \(y\) como la suma de nuestras observaciones, es decir,\(y=\sum_{i=1}^{n}X_i\). Utilizando el teorema de Bayes, podemos expresar nuestras distribuciones de la siguiente manera:
\[\begin{align*} \pi(\lambda) &\propto \lambda^{\alpha-1} e^{\beta\lambda} \\ f_n(x\vert \lambda) & \propto e^{-n\lambda} \lambda^{y} \\ \pi(\lambda\vert X) & \propto \lambda^{\lambda+y-1} e^{(\beta+n)\lambda}. \end{align*}\]
Para este caso, la distribución posterior es \(\lambda|x \sim \Gamma(y+1,n+2)\). La varianza de la distribución Gamma está dada por: \[\begin{equation*} \mathrm{Var}(\lambda) = \dfrac{\alpha}{\beta^2} = \dfrac{y+1}{(n+2)^2}. \end{equation*}\]
Sustituyendo los valores que tenemos:
\[\begin{eqnarray*} & \frac{y+1}{(n+2)^2} &\leq 0.01 \\ \implies& \frac{1}{(n+2)^2} &\leq \frac{y+1}{(n+2)^2} \leq 0.01 \\ \implies& 100 &\leq (n+2)^2 \\ \implies& n &\geq 8 \end{eqnarray*}\]
Por lo tanto, necesitamos al menos 8 observaciones para alcanzar la varianza deseada de 0.01 en nuestra estimación de \(\lambda\).
Retomemos el caso normal para entender cómo se constrruye la posteriores en este caso.
Teorema 4.2 Si \(X_1,\dots,X_n \sim N(\theta, \sigma^2)\) con \(\sigma^2\) conocido y la previa es \(\theta \sim N(\mu_0,V_0^2)\), entonces \(\theta|X\sim N(\mu_1,V_1^2)\) donde \[\begin{equation*} \mu_1 = \dfrac{\sigma^2\mu_0 + nV_0^2 \bar{X}_n}{\sigma^2 + nV_0^2}, \quad V_1^2 = \dfrac{\sigma^2V_0^2}{\sigma^2 + nV_0^2} \end{equation*}\]
Prueba. Construyamos cada elemento por separado:
Verosimilitud: \[\begin{equation*} f_n(X|\theta) \propto \exp\left[- \dfrac{1}{2\sigma^2} \sum_{i=1}^{n}(X_i-\theta)^2\right] \end{equation*}\] Luego, \[\begin{align*} \sum_{i=1}^n (X_i-\theta)^2 & = \sum_{i=1}^n (X_i-\bar X + \bar X - \theta)^2 \\ & = n(\bar X + \theta)^2 + \underbrace{\sum_{i=1}^n (X_i-\bar X)^2}_{\text{constante con respecto a }\theta} + \underbrace{2 \sum_{i=1}^n (X_i-\bar X)(\bar X - \theta)}_{= 0 \text{ pues } \sum X_i = n\bar X)} \end{align*}\] Entonces \[ f_n(X|\theta) \propto \exp\left[-\dfrac{n}{2\sigma ^2}(\bar X - \theta )^2\right].\]
Previa: \[ \pi(\theta) \propto \exp\left[-\dfrac{1}{2V_0^2}(\theta - \mu_0)^2\right].\]
Posterior: \[ \pi(\theta|X) \propto \exp\left[-\dfrac{n}{2\sigma ^2}(\bar X - \theta )^2-\dfrac{1}{2V_0^2}(\theta - \mu_0)^2\right].\]
Con \(\mu_1\) y \(V_1^2\) definidos anteriormente, se puede comprobar la siguiente identidad:
\[-\dfrac{n}{\sigma ^2}(\bar X - \theta )^2-\dfrac{1}{V_0^2}(\theta - \mu_0)^2= \dfrac{1}{V_1^2}(\theta-\mu_1)^2 + \underbrace{\dfrac{n}{\sigma^2 + nV_0^2}(\bar X_n- \mu_0)^2}_{\text{Constante con respecto a }\theta}\]
Por lo tanto,
\[\pi(\theta|X) \propto \exp\left[-\dfrac{1}{2V_1^2}(\theta -\mu_1)^2\right]\]
Corolario 4.1 Si definimos
\[\mu_1 = \underbrace{\dfrac{\sigma^2}{\sigma^2 + nV_0^2}}_{W_1}\mu_0 + \underbrace{\dfrac{nV_0^2}{\sigma^2 + nV_0^2}}_{W_2} \bar X_n \]
Entonces,
Si \(V_0^2\) y \(\sigma^2\) son fijos, entonces \(W_1 \xrightarrow[n\to \infty]{}0\) (la importancia de la media empírica crece conforme aumenta \(n\)).
Si \(V_0^2\) y \(n\) son fijos, entonces \(W_2 \xrightarrow[\sigma^2\to \infty]{}0\) (la importancia de la media empírica decrece conforme la muestra es menos precisa).
Si \(\sigma^2\) y \(n\) son fijos, entonces \(W_2 \xrightarrow[V_0^2\to \infty]{}1\) (la importancia de la media empírica crece conforma la previa es menos precisa).
Ejemplo 4.10 Consideremos el conjutno de datos que vienen de una distribución normal \(N(\theta, \sigma^2)\) con varianza conocida \(\sigma^2=0.25\). Si asumimos que la media poblacional \(\theta\) tiene una distribución previa \(N(\mu_{0}, V_{0}^2)\) con \(\mu_0=2\) y \(V_0^2=1\). Se nos pide usar actualizar nuestr previa con los siguientes datos:
x <- c(1.28, 0.72, 1.17, 1.31, 1.16, 1.45, 1.08, 1.22, 0.60, 1.32,
1.32, 1.47, 1.24, 1.44, 0.71, 0.51, 0.49, 1.49, 1.38, 1.33,
1.20, 0.86, 0.78, 0.57, 0.95, 1.79, 2.20, 2.27, 1.78, 1.87,
1.83, 2.94, 1.26, 1.16, 1.73, 1.45, 1.31, 1.51, 1.80, 1.47,
1.15, 1.06, 0.97, 2.01, 1.12, 1.39)
ggplot(data.frame(x = x), aes(x = x)) +
geom_histogram(fill = "white", color = "black", bins = 15) +
xlab("x") +
ylab("frecuencia") +
cowplot::theme_cowplot()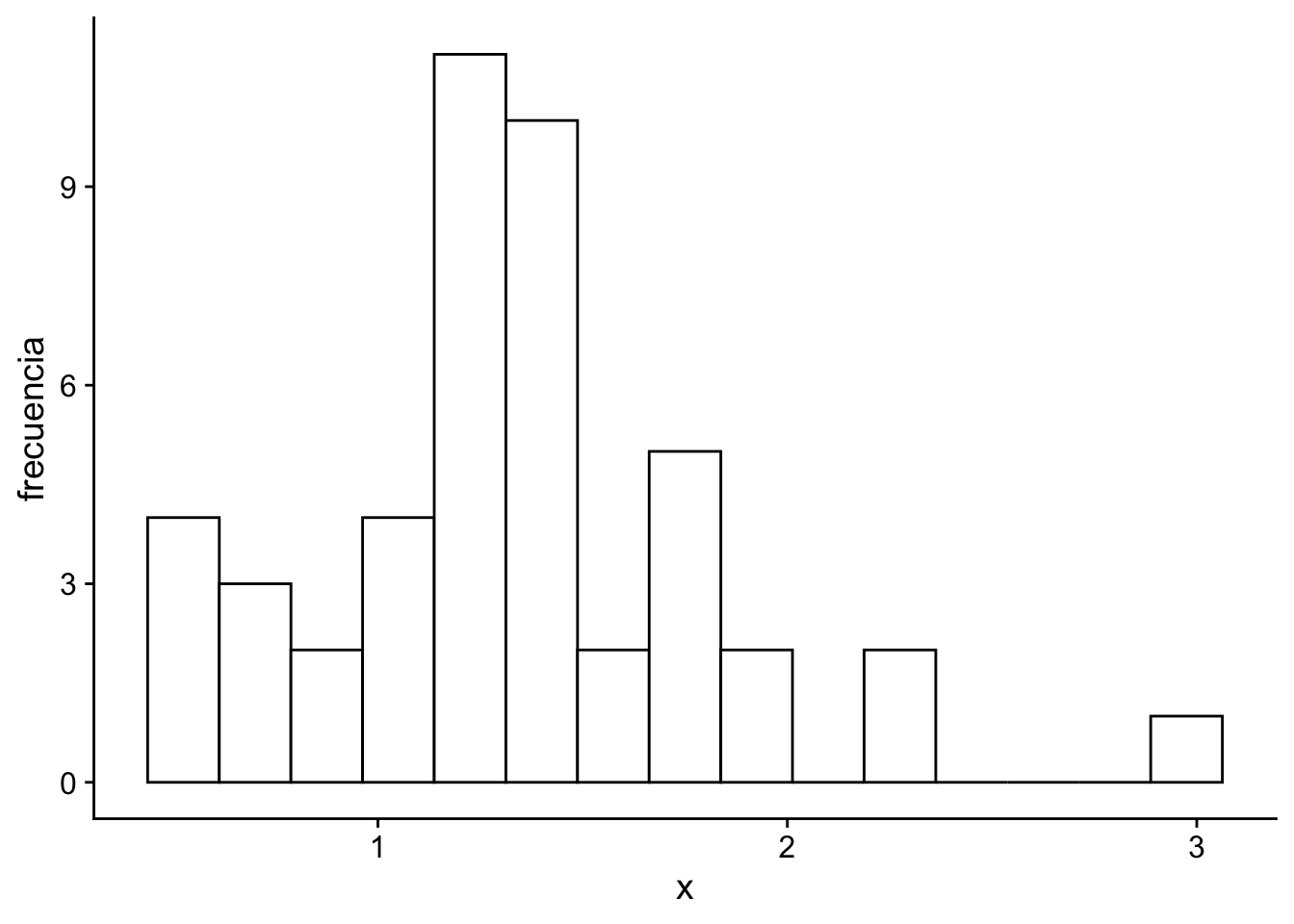
Entonces \(\bar{X}_n = 1.329\) y tenemos que \(n = 46\)
\[\begin{align*} \mu_1 &= \frac{0.25}{0.25+46\times 1} 2 + \frac{46 \times 1}{0.25 + 46 \times 1} 1.329 = 1.333 \end{align*}\]
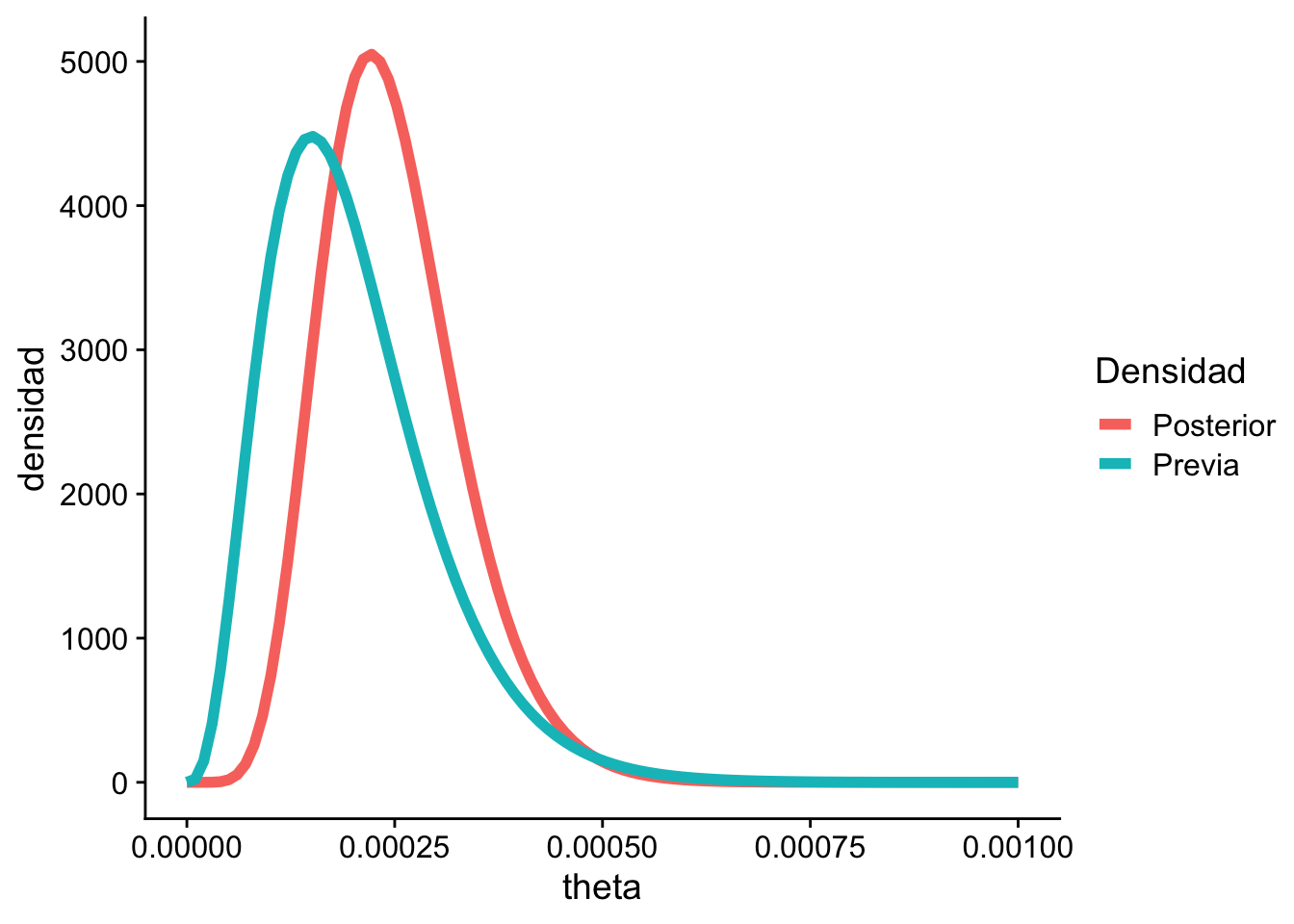
Comparando la previa, la verosimilitud y la posterior, tenemos que:
Ejemplo 4.11 (Determinación de n) Sean \(X_1,\dots, X_n \sim N(\theta,1)\) y \(\theta\sim N(\mu_0,4)\). Sabemos que \[V_1^2 = \dfrac{\sigma^2V_0^2}{\sigma^2 + nV_0^2}. \] Buscamos que \(V_1\leq 0.01\), entonces \[ \dfrac{4}{4n+1}\leq 0.01 \implies n\geq 99.75 \text{ (al menos 100 observaciones)}\]
4.5 Densidades previas impropias
Definición 4.2 Sea \(\pi\) una función positiva cuyo dominio está en \(\Omega\). Si la ingtegral de \(\pi(\theta)\) sobre \(\Omega\) es infinity, i.e. \(\int\pi(\theta)\;d\theta=\infty\); entonces decimos que \(\pi\) es una densidad impropia. Por ejemplo \(\theta \sim \text{Unif}(\mathbb{R})\), \(\lambda \sim \text{Unif}(0,\infty)\).
Observación. Una técnica para seleccionar distribuciones impropia es sustituir los hiperparámetros previos por 0.
Ejemplo 4.12 La siguiente tabla muestra el número de soldados prusianos muertos por una patada de caballo en 14 unidades de combate por 20 años, para contar 280 unidades. La siguiente tabla resume, cuántas de esas unidades tuvieron este tipo de muertes:
| Unidades | Ocurrencias |
|---|---|
| 144 | 0 |
| 91 | 1 |
| 32 | 2 |
| 11 | 3 |
| 2 | 4 |
Verosimilitud: Podemos modelar el número de muertes como una distribución Poisson: \(X_1 = 0, X_2 = 1, X_3 = 1,\dots, X_{280} = 0 \sim \text{Poisson}(\lambda)\).
Previa: Para hacer que la posterior conjugue, entonces \(\lambda \sim \Gamma(\alpha, \beta)\).
Posterior: De acuerdo a lo que hemos visto anteriormente \(\lambda|X \sim \Gamma(y+\alpha, n+\beta) = \Gamma(196 + \alpha, 280 + \beta)\).
El problema acá es que no sabemos cuál valor de \(\alpha\) o \(\beta\) deberíamso tomar. Una opción es tomar \(\alpha = \beta = 0\), lo cual nos da una distribución impropia. En este caso:
\[\begin{align*} \pi(\lambda) &= \dfrac{1}{\Gamma(\alpha)}\beta^\alpha\lambda^{\alpha-1}e^{\beta\lambda} \\ & \propto \lambda^{\alpha-1}e^{-\lambda\beta} \\ &=\dfrac{1}{\lambda} \end{align*}\] donde \(\displaystyle\int_{0}^{\infty}\dfrac{1}{\lambda} d\lambda = \infty\).
Por teorema de Bayes, \[\theta|X \sim \Gamma(196,280)\]
Gráficamente tenemos la versoimilitud, la previa y la posterior:
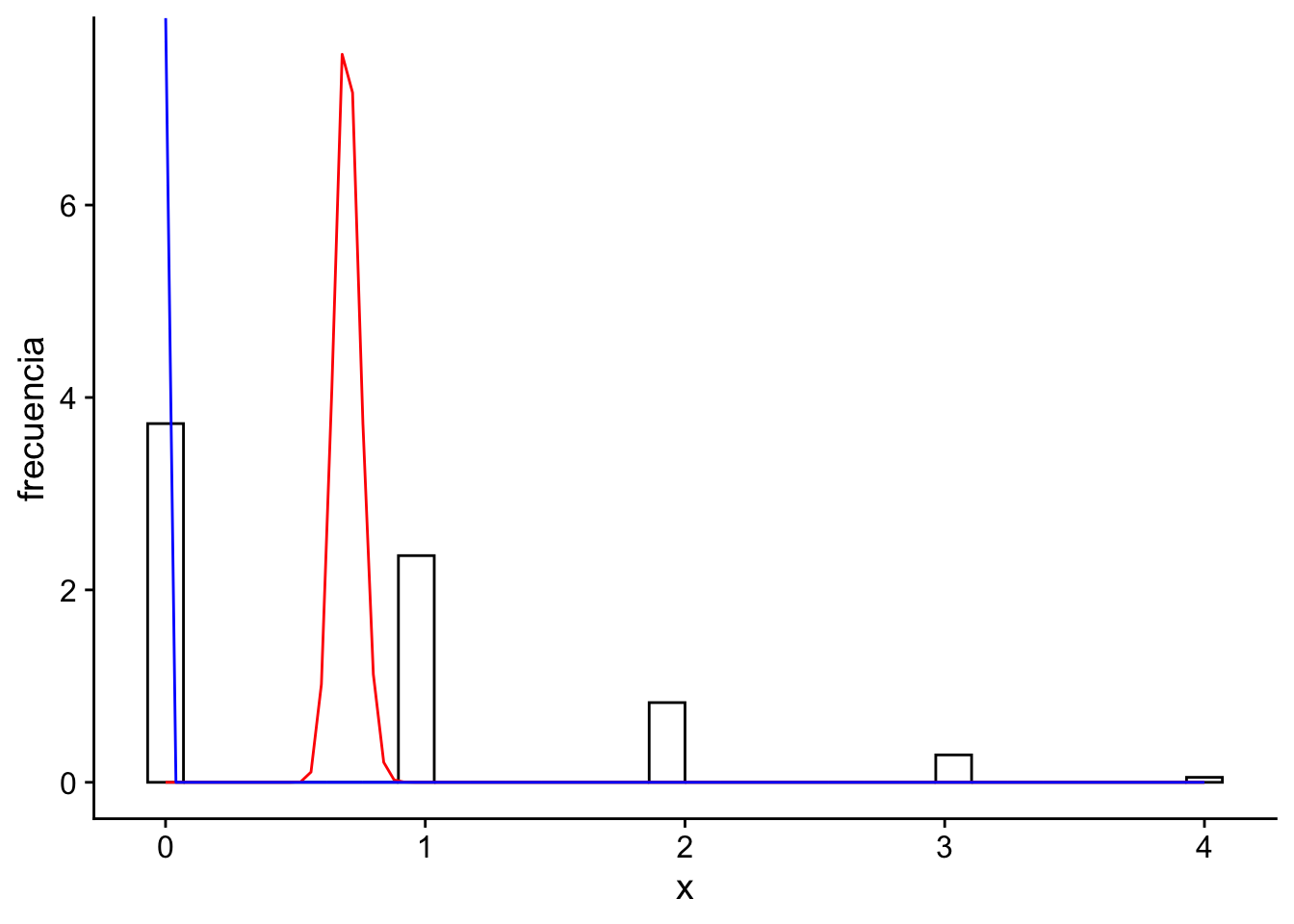
4.6 Funciones de pérdida
Definición 4.3 Sean \(X_1,\dots, X_n\) datos observables cuyo modelo está indexado por \(\theta\in\Omega\). Un estimador de \(\theta\) es cualquier estadístico \(\delta(X_1,\dots, X_n)\).
Definición 4.4
- Estimador \(\to \delta(X_1,\dots,X_n)\).
- Estimación o estimado: \(\delta(X_1,\dots,X_n)(\omega) = \delta(\overbrace{x_1,\dots,x_n}^{datos})\)
Definición 4.5 Una función de pérdida es una función de dos variables: \[ L(\theta,a), \quad \theta \in\Omega\] con \(a\) un número real. Es decir, es lo que se pierde cuando el parámetro es \(\theta\) y se quiere estimar con el valor \(a\).
Asuma que \(\theta\) tiene una previa. La pérdida esperada es \[ \mathbb{E}[L(\theta,a)] = \int_{\Omega}L(\theta, a) \pi(\theta)\;d\theta\] la cual es una función de \(a\), que a su vez es función de \(X_1,\dots,X_n\). Asuma que \(a\) se selecciona el minimizar esta esperanza. A ese estimador \(a = \delta^*(X_1,\dots, X_n)\) se le llama estimador bayesiano, si ponderamos los parámetros con respecto a la posterior.
\[\mathbb{E}[L(\theta, \delta^*)|X] = \int_{\Omega}L(\theta, a) \pi(\theta)\;d\theta = \min_a \mathbb{E}[L(\theta|a)X]. \]
4.6.1 Función de pérdida cuadrática
Si \(L(\theta,a) = (\theta-a)^2\), entonces la pérdida esperada es
\[\begin{align*} \mathbb{E}[L(\theta,a)] &= \int_{\Omega}(\theta-a)^2 \pi(\theta\mid X)\;d\theta \\ &= \int_{\Omega}\theta^2\pi(\theta\mid X)\;d\theta - 2a\int_{\Omega}\theta\pi(\theta\mid X)\;d\theta + a^2\int_{\Omega}\pi(\theta \mid X)\;d\theta \\ &= \mathbb{E}[\theta^2\mid X] - 2a\mathbb{E}[\theta\mid X] + a^2 \\ \end{align*}\]
Note que la pérdida esperada es una función cuadrática en \(a\). Para minimizarla, derivamos con respecto a \(a\) e igualamos a 0.
\[\begin{align*} \dfrac{\partial}{\partial a} \mathbb{E}[L(\theta,a)] &= -2\mathbb{E}[\theta\mid X] + 2a = 0 \\ \implies a &= \mathbb{E}[\theta\mid X] \end{align*}\]
En otras palabras el estimador bayesiano es la esperanza posterior. Formalmente:
\[\begin{equation*} \delta^*(X_1,\dots, X_n) = \mathbb{E}[\theta|X] \text{ cuando } L(\theta,a) = (\theta-a)^2. \end{equation*}\]
Ejemplo 4.13 Sea \(X_1,\dots, X_n \sim \text{Ber}(\theta)\), \(\theta \sim \text{Beta}(\alpha,\beta) \implies \theta|X \sim \text{Beta}(\alpha+y,\beta+n-y)\).
El estimador de \(\theta\) es \[\begin{align*} \delta(X_1,\dots, X_n) &= \dfrac{\alpha+y}{\alpha + \beta + n} \\ &= \overbrace{\dfrac{\alpha}{\alpha + \beta} }^{\text{Esperanza previa}}\cdot \dfrac{\alpha +\beta}{\alpha +\beta + n} + \overbrace{\dfrac{y}{n}}^{\bar X}\cdot \dfrac{n}{\alpha +\beta + n}. \end{align*}\]
4.6.2 Función de pérdida absoluta
Si \(L(\theta,a) = |\theta-a|\), entonces la pérdida esperada es
\[\begin{align*} \mathbb{E}[L(\theta,a)|X] &= \int_{-\infty}^{+\infty}|\theta-a|\pi(\theta|X)\;d\theta \\ &= \int_{a}^{+\infty}(\theta-a)\pi(\theta|X)\;d\theta + \int_{-\infty}^{a}(a-\theta)\pi(\theta|X)\;d\theta\\ &= -\int_{+\infty}^{a}(\theta-a)\pi(\theta|X)\;d\theta + \int_{-\infty}^{a}(a-\theta)\pi(\theta|X)\;d\theta\\ \end{align*}\]
La regla de Leibniz dice que si \(F(x) = \int_{-\infty}^{x}f(x,t)\;dt\), entonces
\[\begin{equation*} \dfrac{d}{dx}F(x) = f(x,x) + \int_{-\infty}^{x}\dfrac{\partial}{\partial x}f(x,t)\;dt \end{equation*}\]
Por lo tanto para este caso tenemos
\[\begin{align*} \dfrac{d}{da}\mathbb{E}[L(\theta,a)|X] &= -\left((a-a)\pi(a|X) - \int_{+\infty}^{a}\pi(\theta|X)\;d\theta\right) \\ & \qquad + (a-a) \pi(a|X) + \int_{-\infty}^{a}\pi(\theta|X)\;d\theta \\ &= \int_{-\infty}^{a} \pi(\theta|X)\;d\theta - \int_{a}^{+\infty} \pi(\theta|X)\;d\theta \\ \end{align*}\]
Igualando esta última expresión a 0, tenemos que
\[\begin{align*} \int_{-\infty}^{a} \pi(\theta|X)\;d\theta &= \int_{a}^{+\infty} \pi(\theta|X)\;d\theta \\ \implies F_{\theta\mid X}(a) &= \int_{-\infty}^{a} \pi(\theta|X)\;d\theta = \dfrac{1}{2} \\ \end{align*}\]
La mediana es el punto de \(m\) tal que \(F_{\theta\mid X}(m) = \dfrac{1}{2}\).
Observación. Bajo la función de pérdida absoluta, el estimador bayesiano es la mediana posterior.
Ejemplo 4.14 Para el caso Bernoulli. \[ \dfrac{1}{\text{Beta}(\alpha+y, \beta+n-y)}\int_{-\infty}^{X_{0.5}}\theta^{\alpha+y-1} (1-\theta)^{\beta+n-y-1}\;d\theta = \dfrac12\] Encontrar el valor que \(X_{0.5}\) que resuelve esta ecuación es díficil y se debe hacer usando métodos numéricos.
Por ejemplo, si tuvieramos que la posterior fuera una \(\mathrm{Beta}(22,18)\) entonces podríamos resolverlo en R de la siguiente forma
encuentra_mediana_beta <- function(q, alpha, beta) {
abs(pbeta(q, alpha, beta) - 1 / 2)
}
opt <- optimize(encuentra_mediana_beta, c(0, 1), alpha = 22, beta = 18)
opt$minimum[1] 0.5508349Note que la media sería \(\frac{22}{40}=0.55\).
4.6.3 Otras funciones de pérdida
\(L(\theta,a) = |\theta-a|^k\), \(k\ne 1,2\), \(0<k<1\).
\(L(\theta,a) = \lambda(\theta)|\theta-a|^2\) (\(\lambda(\theta)\) penaliza la magnitud del parámetro).
\(L(\theta,a)=\begin{cases}3(\theta-a)^2 & \theta\leq a \text{ (sobreestima)}\\ (\theta-a)^2&\theta\geq a \text{ (subestima)} \end{cases}\)
4.7 El estimador de bayes para muestras grandes
4.7.1 Efecto de diferentes previas
Ejemplo 4.15 Suponga que se tiene un examen con ítemes malos (proporción: \(\theta\)), \(\theta \in [0,1]\). Se decide usar una función de pérdida cuadrática. El tamaño de muestra son \(n=100\) ítemes, de los cuales \(y=10\) están malos.
\[ X_1,\dots,X_n\sim \text{Ber}(\theta)\]
Usemos diferentes previas para ver su efecto en los estimadores
- Primer previa. \(\alpha = \beta = 1\) (Beta). El estimador bayesiano corresponde a
\[ \mathbb{E}[\theta|X] = \dfrac{\alpha+y}{\alpha+\beta+n} = \dfrac{1+10}{2+100} = 0.108\]
- Segunda previa. \(\alpha =1, \beta=2 \implies \pi(\theta) = 2e^{-2\theta}, \theta >0\).
\[ \mathbb{E}[\theta|X] = \dfrac{1+10}{1+2+100} = \dfrac{11}{103}=0.107\]
Las previas son muy diferentes una de la otra, pero el estimador final es muy parecido debido a la cantidad de datos. Compare esto con la media empírica \(\bar X_n = \dfrac{10}{100} = 0.1\).
4.7.2 Consistencia
Definición 4.6 Un estimador de \(\theta\) \(\delta(X_1,\dots, X_n)\) es consistente si \[\delta(X_1,\dots, X_n)\xrightarrow[n\to \infty]{\mathbb{P}}\theta.\]
Bajo pérdida cuadrática, \(\mathbb{E}[\theta|X] = W_1\mathbb{E}[\theta] + X_2\bar X_n = \delta^*\). Sabemos, por ley de grandes números, que \(\bar X_n \xrightarrow[n\to \infty]{\mathbb{P}}\theta\). Además, \(W_1\xrightarrow[n\to \infty]{}0\) y \(W_2\xrightarrow[n\to \infty]{}1\).
En los ejemplos que hemos analizado \[\delta^* \xrightarrow[n\to \infty]{\mathbb{P}}\theta \]
Teorema 4.3 Bajo condiciones mencionadas anteriormente, los estimadores bayesianos son consistentes.
De forma general podemos definir un estimador de la siguiente forma
Definición 4.7 (Estimador) Si \(X_1,\dots, X_n\) es una muestra en un modelo indexado por \(\theta\), \(\theta \in \Omega\) (\(k\)-dimensiones), sea
\[h:\Omega \to H \subset \mathbb{R}^d.\]
Defina \(\psi = h(\theta)\). Un estimador de \(\psi\) es una función o estadístico \(\delta(X_1,\dots, X_n) \in H\).
Observación. Ojo, la definición de estimador solo requiere que el parámetro \(\psi\) y el estimador \(\delta\) pertenenzca el mismo espacio. Puede ser que un \(\delta_1\) sea mejor que un \(\delta_2\).
Ejemplo 4.16 \(X_1,\dots, X_n \sim \text{Exp}(\theta)\), \(\theta|X \sim \Gamma(\alpha,\beta) = \Gamma (4,8.6)\). La característica de interés es \(\psi = \dfrac{1}\theta\), el valor esperado del tiempo de fallo.
Es estimador se calcula de la siguiente manera:
\[\begin{align*} \delta(x) = \mathbb{E}[\psi|x] & = \int_{0}^\infty \dfrac{1}\theta\pi(\theta|x)\;d\theta\\ & = \int_{0}^\infty \dfrac{1}\theta \dfrac{8.6^4}{\Gamma(4)} \theta^3e^{-8.6\theta}\;d\theta\\ &=\dfrac{8.6^4}{6} \int_{0}^\infty \theta^2 e^{-8.6\theta}\;d\theta\\ &= \dfrac{8.6^4}{6}\frac{\Gamma(3)}{8.6^3} \\ & = \dfrac{8.6^4}{6}\dfrac{2}{8.6^3} \\ & = 2.867 \text{ unidades de tiempo.} \end{align*}\]
Por otro lado, vea que \(\mathbb{E}(\theta|X) = \dfrac{4}{8.6}\). El estimador plug-in correspondería a \[\dfrac{1}{\mathbb{E}(\theta|X)} = \dfrac{8.6}{4} = 2.15.\]
4.8 Laboratorio
Lo primero es cargar los paquetes necesarios que usaremos en todo el curso
library(tidyverse)4.8.1 Distribución previa
En nuestro ejemplo se tenía que \(\mathbb E [\theta] = 0.0002\) y \(\mathrm{Var}(\theta) = 0.001\). Suponiendo que \(\theta\) es gamma se puede resolver el sistema de ecuaciones obtenemos que \(\beta=20000\) y \(\alpha=4\).
alpha_previa <- 4
beta_previa <- 20000
ggplot(data = data.frame(x = c(0, 1e6)), aes(x)) +
stat_function(
fun = dgamma,
args = list(shape = alpha_previa, scale = beta_previa), linewidth = 2
) +
ylab("") +
scale_y_continuous(breaks = NULL) +
theme_minimal()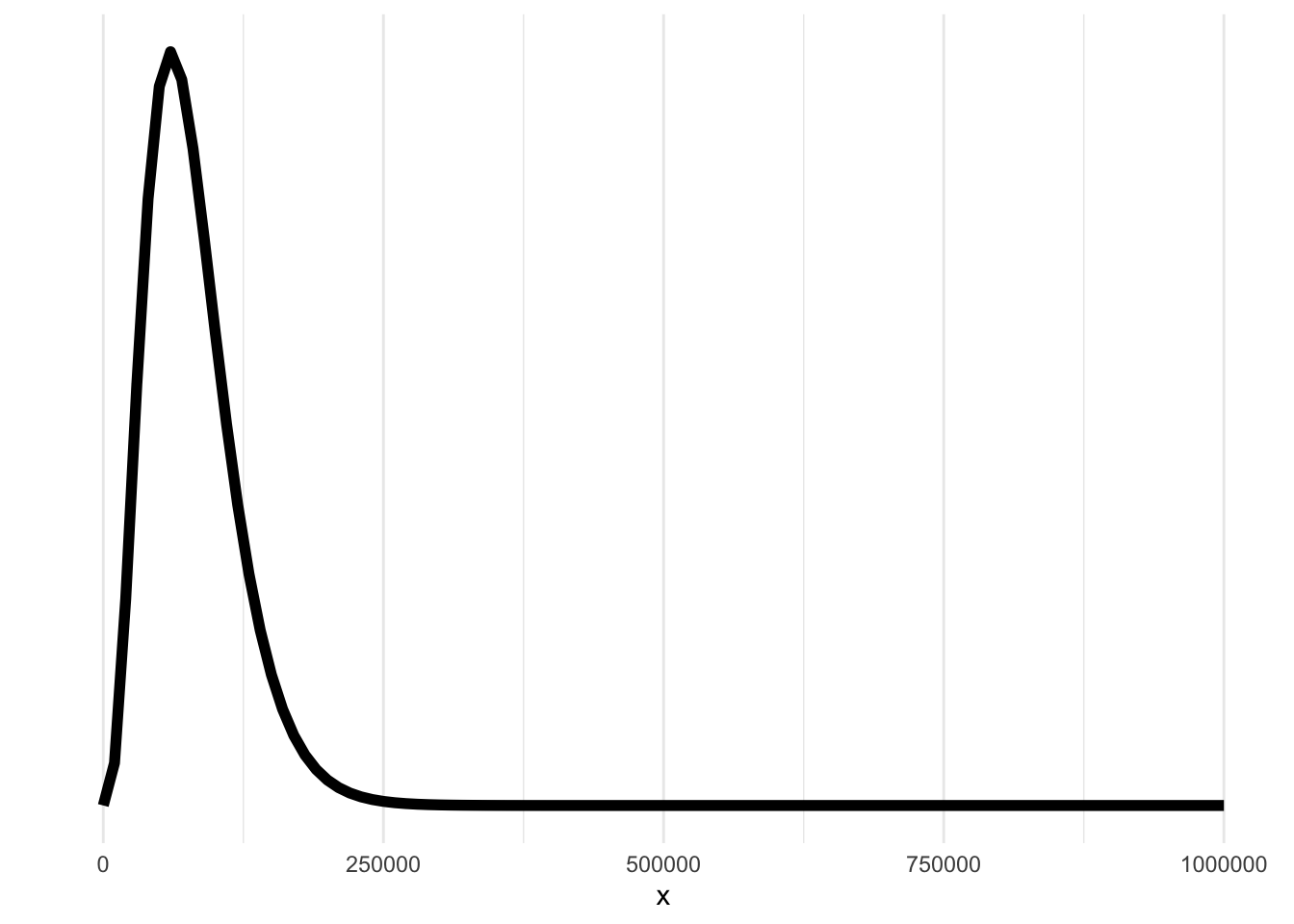
4.8.2 Distribución conjunta
Asumiendo que tenemos algunos datos \(X_1, ..., X_n\), asumimos que estos son exponencial recordando que \(\mathbb E [X] = 1/\theta\), entonces una aproximación de esta densidad es
x <- c(2911, 3403, 3237, 3509, 3118)
theta <- 1 / mean(x)
ggplot(data = data.frame(x = c(0, 1e5)), aes(x)) +
stat_function(fun = dexp, args = list(rate = theta), linewidth = 2) +
ylab("") +
scale_y_continuous(breaks = NULL) +
theme_minimal()
4.8.3 Distribución posterior
Según los contenidos del curso, se puede estimar los parámetros de la densidad posterior de la forma
(y <- sum(x))[1] 16178(n <- length(x))[1] 5(alpha_posterior <- n + alpha_previa)[1] 9(beta_posterior <- beta_previa + y)[1] 36178ggplot(data = data.frame(x = c(0, 7.5e5)), aes(x)) +
stat_function(
fun = dgamma,
args = list(shape = alpha_previa, scale = beta_previa),
aes(color = "Previa"), linewidth = 2
) +
stat_function(
fun = dgamma,
args = list(shape = alpha_posterior, scale = beta_posterior),
aes(color = "Posterior"), linewidth = 2
) +
stat_function(
fun = dexp,
args = list(rate = theta), aes(color = "Verosimilitud"), linewidth = 2
) +
ylim(0, 1.5e-5) +
cowplot::theme_cowplot()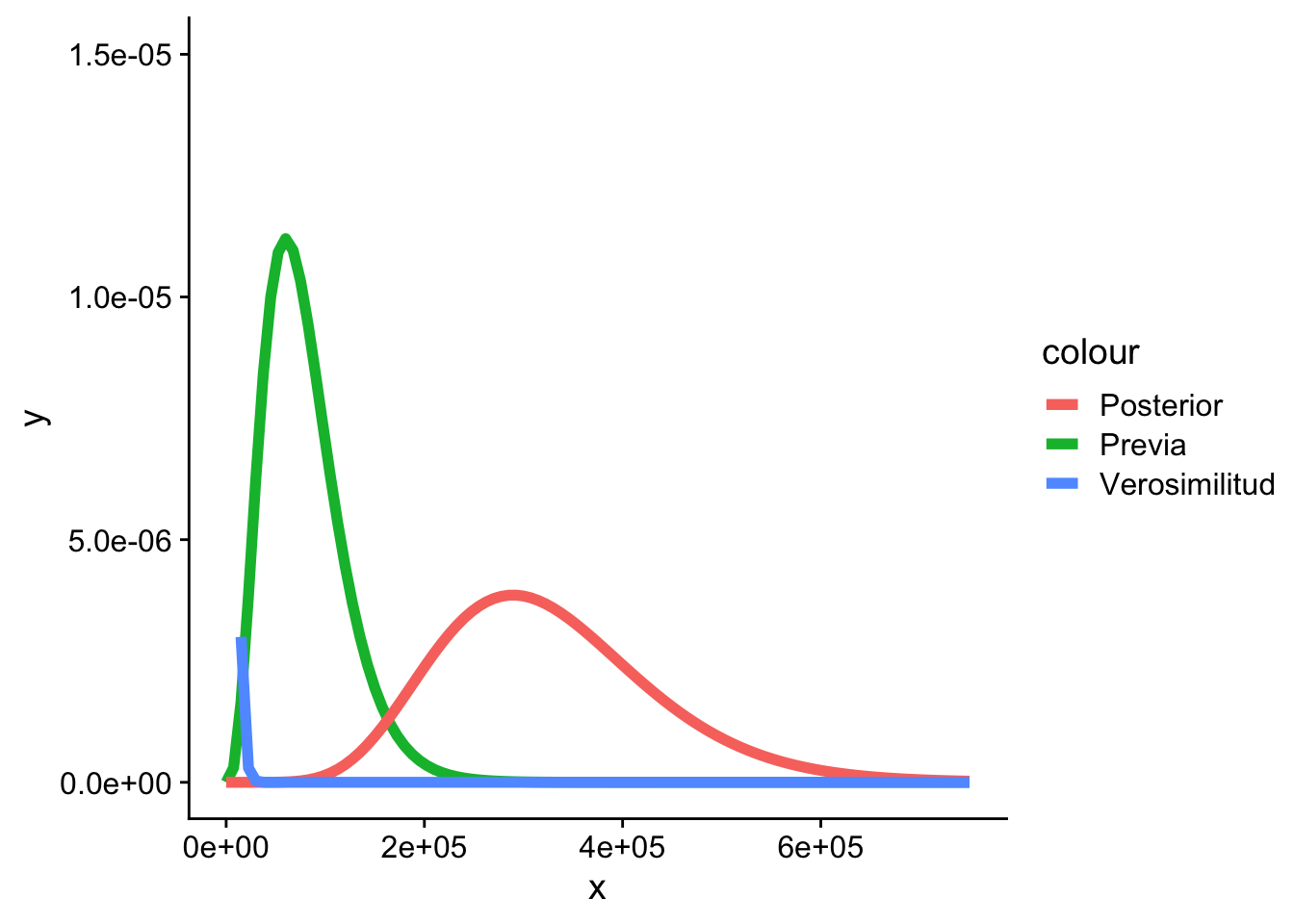
4.8.4 Agregando nuevos datos
Si tenemos un 6to dato, y queremos ver cual es su distribución posterior. Lo primero es estimar la densidad posterior de este 6to dato, pero asumiendo que la previa es la densidad que obtuvimos en el caso anterior.
Suponga que \(X_6 = 3000\)
(alpha_previa <- alpha_posterior)[1] 9(beta_previa <- beta_posterior)[1] 36178(alpha_posterior <- alpha_previa + 1)[1] 10(beta_posterior <- beta_previa + 3000)[1] 39178ggplot(data = data.frame(x = c(0, 1e6)), aes(x)) +
stat_function(
fun = dgamma,
args = list(shape = 4, scale = 20000), aes(color = "Previa #1"),
linewidth = 2
) +
stat_function(
fun = dgamma,
args = list(shape = alpha_previa, scale = beta_previa),
aes(color = "Previa #2"), linewidth = 2
) +
stat_function(
fun = dgamma,
args = list(shape = alpha_posterior, scale = beta_posterior),
aes(color = "Posterior"), linewidth = 2
) +
ylim(0, 1.5e-5) +
cowplot::theme_cowplot()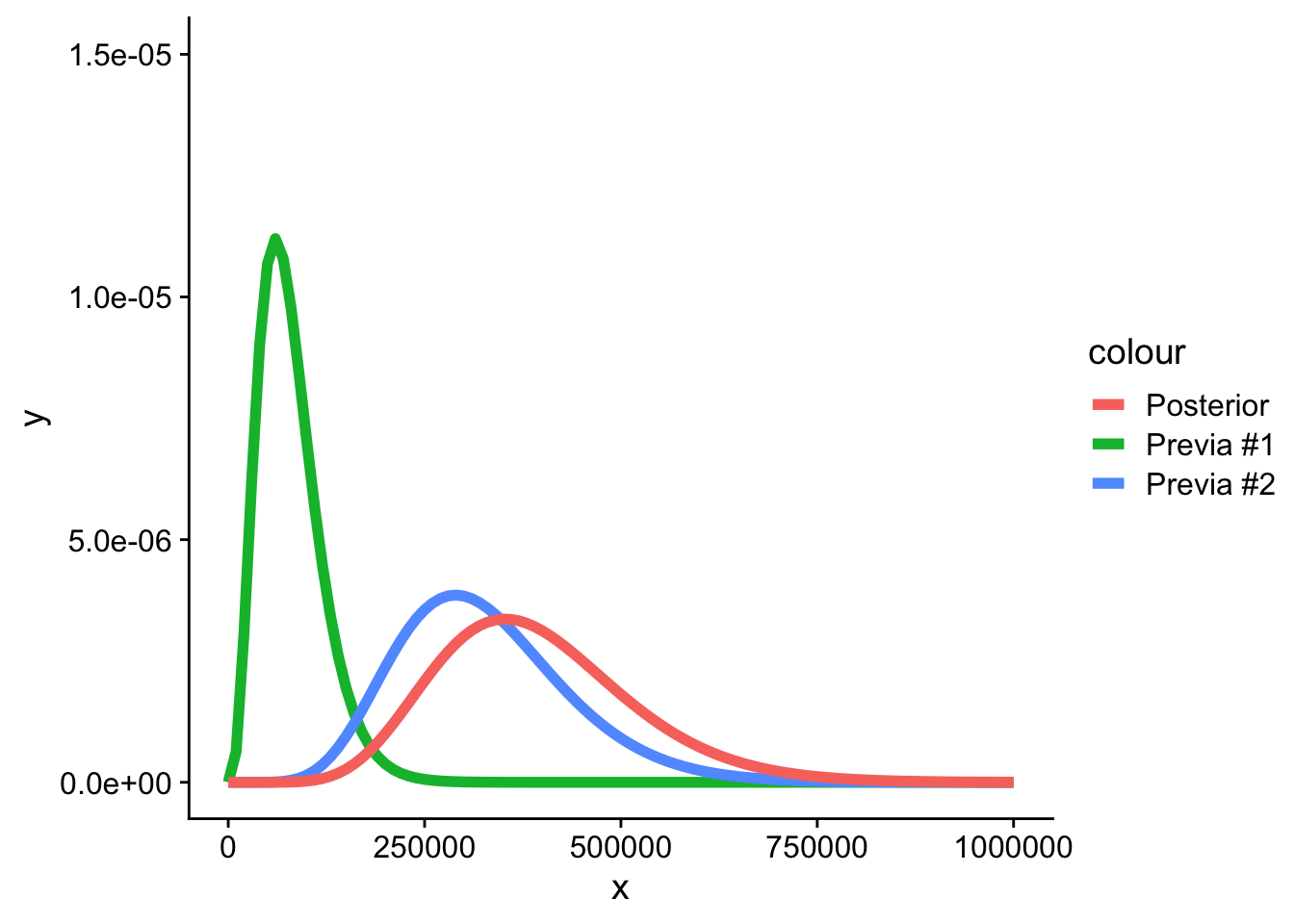
4.8.5 Familias conjugadas normales
Si tenemos pocos datos, la información previa es la que “prevalece”.
x <- rnorm(n = 3, mean = 10, sd = 1)
(mu <- mean(x))[1] 9.528419(sigma <- sd(x))[1] 0.5508148(n <- length(x))[1] 3(mu_previa <- 0)[1] 0(sigma_previa <- 1)[1] 1mu_posterior <- ((sigma^2) / (sigma^2 + n * sigma_previa^2)) * mu_previa +
((n * sigma_previa^2) / (sigma^2 + n * sigma_previa^2)) * mu
mu_posterior[1] 8.653291sigma2_posterior <- (sigma^2 * sigma_previa^2) / (sigma^2 + n * sigma_previa^2)
sigma2_posterior[1] 0.09184394ggplot(data = data.frame(x = c(-5, 15)), aes(x)) +
stat_function(
fun = dnorm,
args = list(mean = mu_previa, sd = sigma_previa),
aes(color = "Previa"), linewidth = 2
) +
stat_function(
fun = dnorm,
args = list(mean = mu_posterior, sd = sqrt(sigma2_posterior)),
aes(color = "Posterior"), linewidth = 2
) +
stat_function(
fun = dnorm,
args = list(mean = mu, sd = sigma),
aes(color = "Verosimilitud"), linewidth = 2
) +
cowplot::theme_cowplot()
Con más datos, la distribución se ajusta a esto y le quita importancia a la información previa.
x <- rnorm(n = 100, mean = 10, sd = 1)
(mu <- mean(x))[1] 9.913615(sigma <- sd(x))[1] 0.9517395(n <- length(x))[1] 100(mu_previa <- 0)[1] 0(sigma_previa <- 1)[1] 1mu_posterior <- ((sigma^2) / (sigma^2 + n * sigma_previa^2)) * mu_previa +
((n * sigma_previa^2) / (sigma^2 + n * sigma_previa^2)) * mu
mu_posterior[1] 9.824623sigma2_posterior <- (sigma^2 * sigma_previa^2) / (sigma^2 + n * sigma_previa^2)
sigma2_posterior[1] 0.008976769ggplot(
data = data.frame(x = c(-5, 15)),
aes(x)
) +
stat_function(
fun = dnorm,
args = list(mean = mu_previa, sd = sigma_previa),
aes(color = "Previa"), linewidth = 2
) +
stat_function(
fun = dnorm,
args = list(mean = mu_posterior, sd = sqrt(sigma2_posterior)),
aes(color = "Posterior"), linewidth = 2
) +
stat_function(
fun = dnorm,
args = list(mean = mu, sd = sigma),
aes(color = "Verosimilitud"), linewidth = 2
) +
cowplot::theme_cowplot()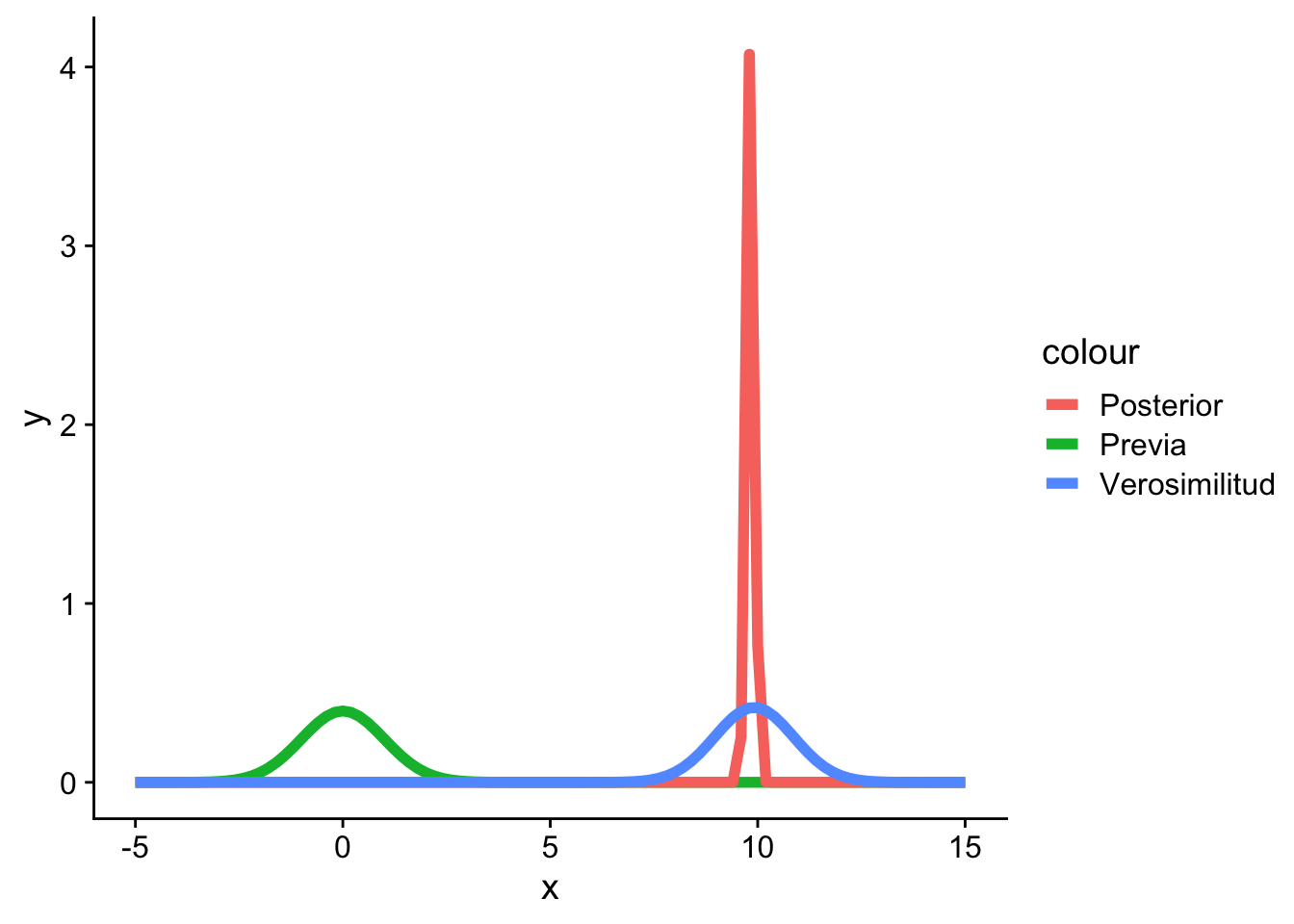
Si los datos por si solo son muy variable, la posterior tiende a parecerse a la distribución previa en lugar que a la verosimilitud.
x <- rnorm(n = 10, mean = 10, sd = 5)
(mu <- mean(x))[1] 9.279006(sigma <- sd(x))[1] 5.280473(n <- length(x))[1] 10(mu_previa <- 0)[1] 0(sigma_previa <- 1)[1] 1mu_posterior <- ((sigma^2) / (sigma^2 + n * sigma_previa^2)) * mu_previa +
((n * sigma_previa^2) / (sigma^2 + n * sigma_previa^2)) * mu
mu_posterior[1] 2.44936sigma2_posterior <- (sigma^2 * sigma_previa^2) / (sigma^2 + n * sigma_previa^2)
sigma2_posterior[1] 0.7360321ggplot(
data = data.frame(x = c(-5, 15)),
aes(x)
) +
stat_function(
fun = dnorm,
args = list(mean = mu_previa, sd = sigma_previa),
aes(color = "Previa"), linewidth = 2
) +
stat_function(
fun = dnorm,
args = list(mean = mu_posterior, sd = sqrt(sigma2_posterior)),
aes(color = "Posterior"), linewidth = 2
) +
stat_function(
fun = dnorm,
args = list(mean = mu, sd = sigma),
aes(color = "Verosimilitud"), linewidth = 2
) +
cowplot::theme_cowplot()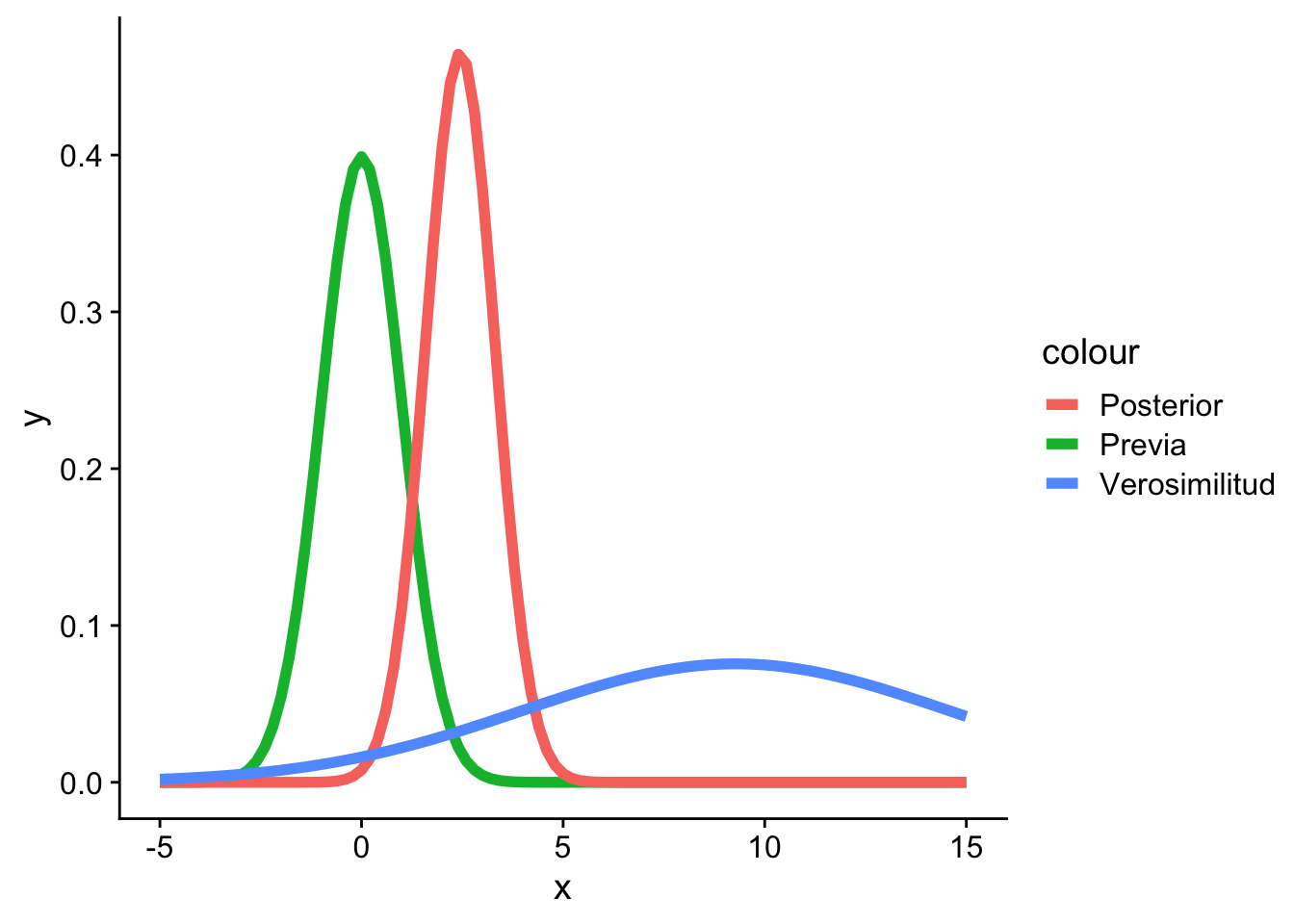
4.8.6 Funciones de pérdida
Lo más importante acá es que dependiendo de la función de pérdida podemos construir una estimador para \(\theta\). En el caso de los componentes electrónicos recordemos que la posterior nos daba
alpha <- 9
beta <- 36178- Pérdida cuadrática: Recordemos que la media de una gamma es \(\alpha/\beta\) entonces
(theta <- alpha / beta)[1] 0.00024877Y por lo tanto el tiempo promedio del componente electrónico es \(1/\theta\)=4019.7777778.
- Pérdidad absoluta: La distribución Gamma no tiene una forma cerrada para la mediana, por que se puede aproximar así,
m <- rgamma(n = 1000, scale = beta, shape = alpha)
(theta <- median(m))[1] 316198.3Y por lo tanto el tiempo promedio del componente electrónico es \(1/\theta\)=3.1625728^{-6}.
Observación. En este caso la pérdida cuadrática ajusta mejor ya que la distribución que la pérdida absoluta ya que la distribución NO es simétrica. En el caso simétrico los resultados serían muy similares.
4.8.7 Caso concreto
Suponga que se que quiere averiguar si los estudiantes de cierto colegio duermen más de 8 horas o menos de 8 horas.
Para esto primero cargaremos el siguiente paquete,
library(LearnBayes)Suponga que se hace una encuesta a 27 estudiantes y se encuentra que 11 dicen que duermen más de 8 horas diarias y el resto no. Nuestro objetivo es encontrar inferencias sobre la proporción \(p\) de estudiantes que duermen al menos 8 horas diarias. El modelo más adecuado es
\[ f(x \vert p) \propto p^s (1-p)^f \]
donde \(s\) es la cantidad de estudiantes que duermen más de 8 horas y \(f\) los que duermen menos de 8 horas.
Una primera aproximación para la previa es usar una distribución discreta. En este caso, el investigador asigna una probabilidad a cierta cantidad de horas de sueño, según su experiencia. Así, por ejemplo:
p <- seq(0.05, 0.95, by = 0.1)
prior <- c(1, 5.2, 8, 7.2, 4.6, 2.1, 0.7, 0.1, 0, 0)
prior <- prior/sum(prior)
plot(p, prior, type = "h", ylab="Probabilidad Previa")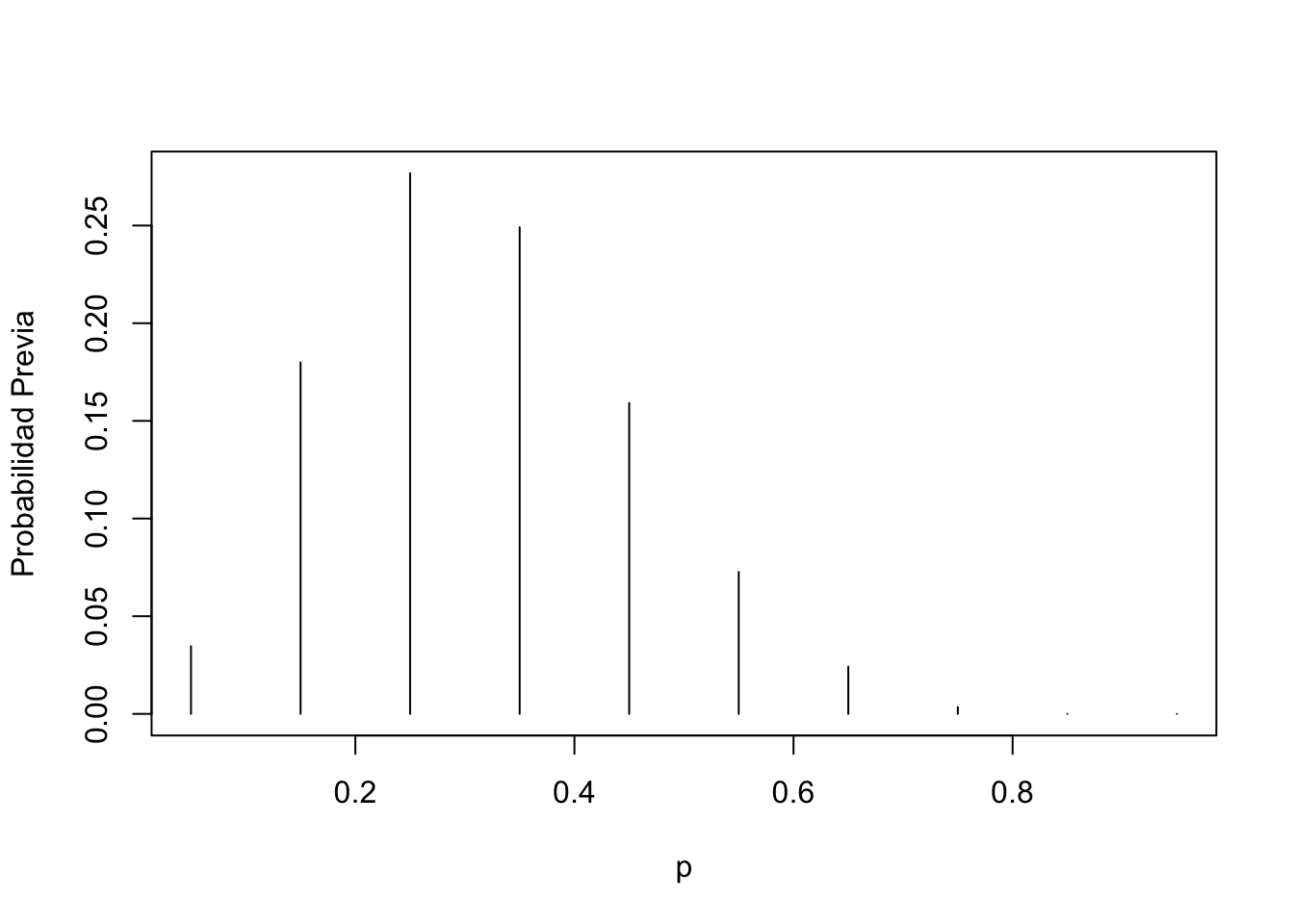
El paquete LearnBayes tiene la función pdisc que estima la distribución posterior para una previa discreta binomial. Recuerde que el valor 11 representa la cantidad de estudiantes con más de 8 horas de sueño y 16 lo que no duermen esa cantidad.
data <- c(11, 16)
post <- pdisc(p, prior, data)
round(cbind(p, prior, post),2) p prior post
[1,] 0.05 0.03 0.00
[2,] 0.15 0.18 0.00
[3,] 0.25 0.28 0.13
[4,] 0.35 0.25 0.48
[5,] 0.45 0.16 0.33
[6,] 0.55 0.07 0.06
[7,] 0.65 0.02 0.00
[8,] 0.75 0.00 0.00
[9,] 0.85 0.00 0.00
[10,] 0.95 0.00 0.00Y podemos ver la diferencia entre la previa (negro) y la posterior (roja),
plot(p, post, type = "h", col = "red")
lines(p + 0.01, prior , type = "h")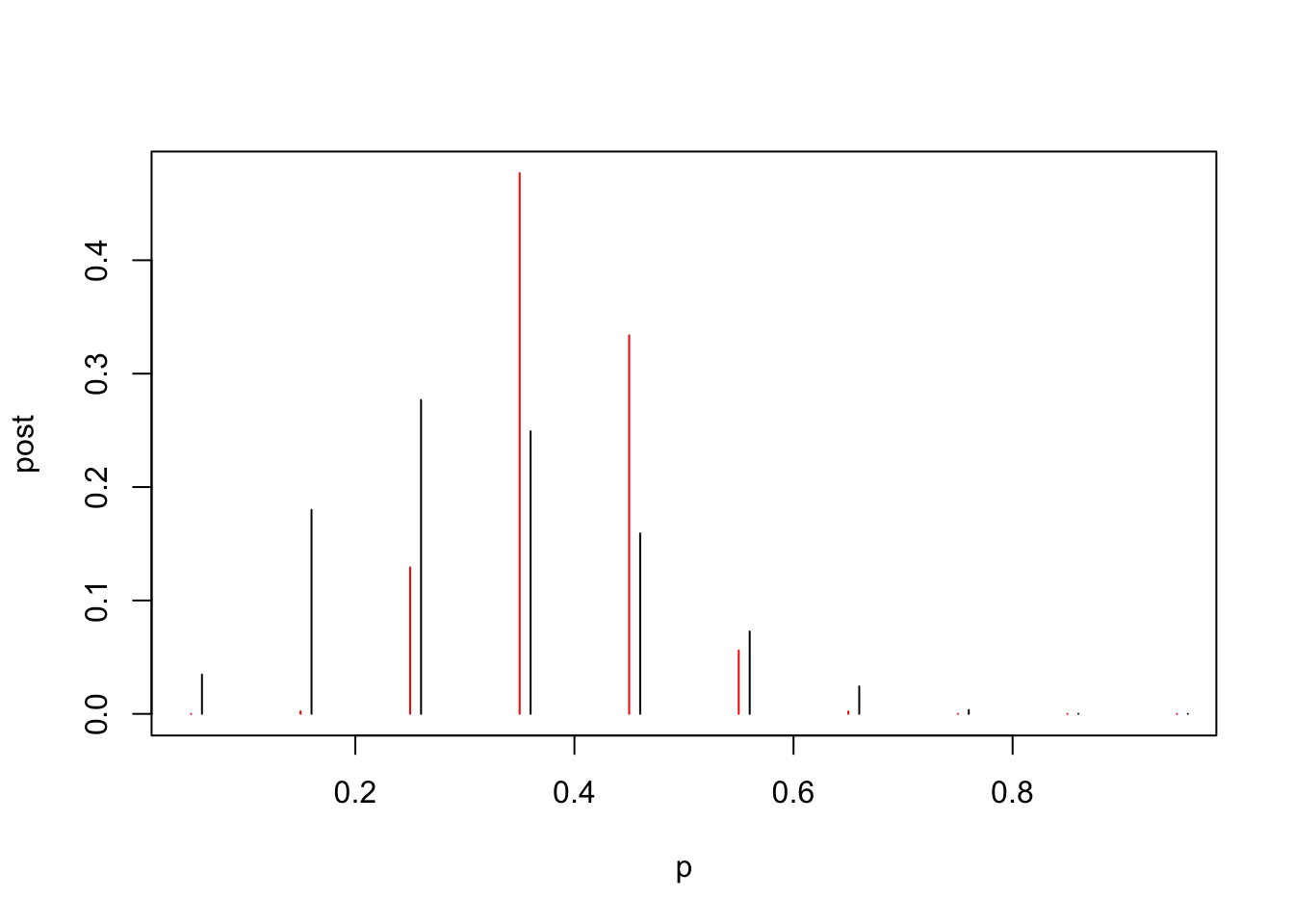
¿Qué se puede deducir de estos resultados?
Ejercicio 4.1 Suponga que se tiene la base de datos studentdata. Realice los cálculos anteriores con esos datos,
data("studentdata")
horas_sueno <- studentdata$WakeUp - studentdata$ToSleep
horas_sueno <- na.omit(horas_sueno)
summary(horas_sueno) Min. 1st Qu. Median Mean 3rd Qu. Max.
2.500 6.500 7.500 7.385 8.500 12.500 hist(horas_sueno, main = "")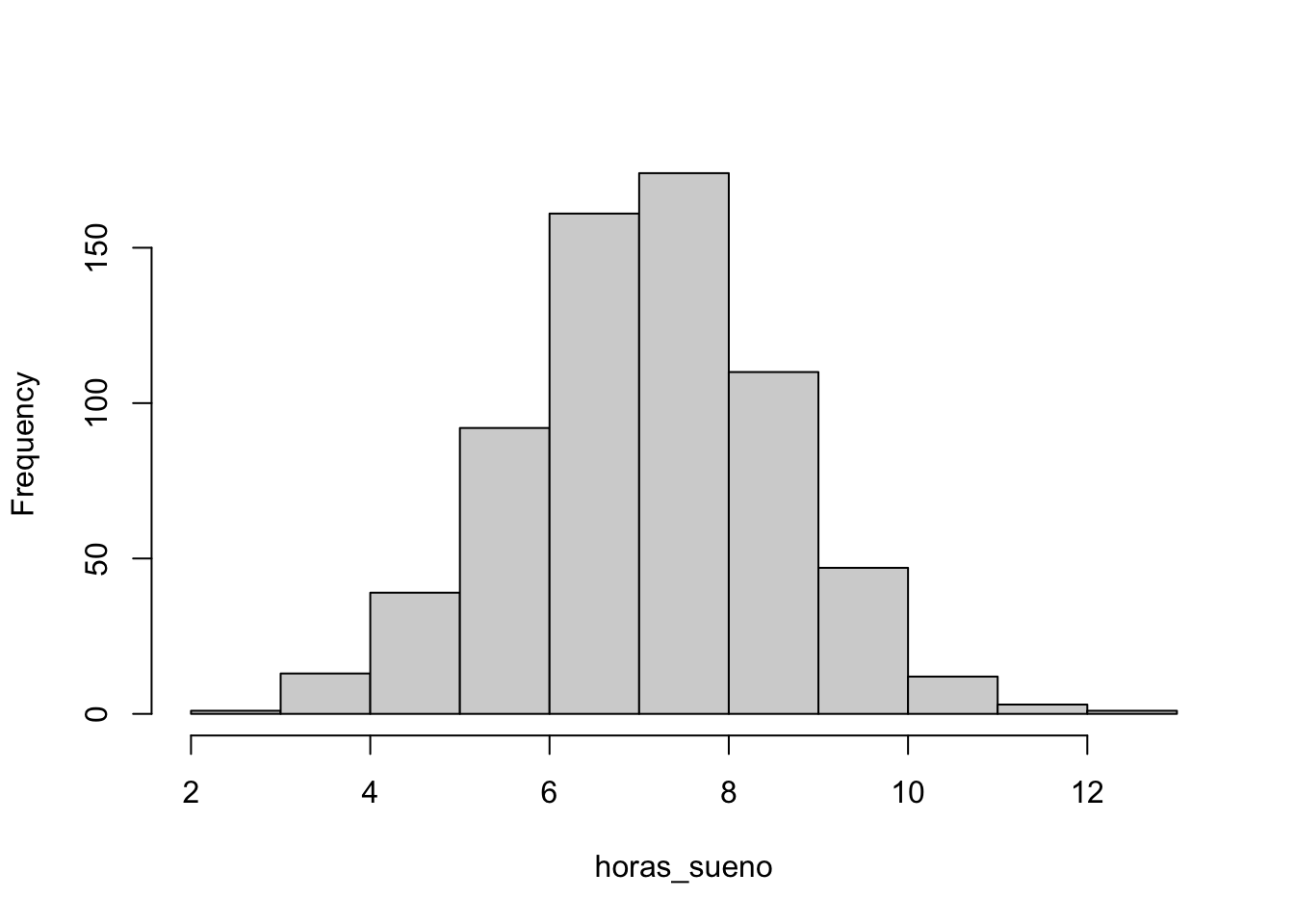
Ahora supongamos que se tiene quiere ajustar una previa continua a este modelo. Para esto usaremos una distribución Beta con parámetros \(\alpha\) y \(\beta\), de la forma
\[ pi(p\vert \alpha, \beta) \propto p^{1-\alpha} (1-p)^{1-\beta}. \]
El ajuste de los parámetro de la Beta depende mucho de la información previa que se tenga del modelo. Una forma fácil de estimarlo es a través de cuantiles con los cuales se puede reescribir estos parámetros. Para una explicación detallada revisar https://stats.stackexchange.com/a/237849
En particular, suponga que se cree que el \(50\%\) de las observaciones la proporción será menor que 0.3 y que el \(90\%\) será menor que 0.5.
Para esto ajustaremos los siguientes parámetros
quantile2 <- list(p = .9, x = .5)
quantile1 <- list(p = .5, x = .3)
(ab <- beta.select(quantile1, quantile2))[1] 3.26 7.19a <- ab[1]
b <- ab[2]
s <- 11
f <- 16En este caso se obtendra la distribución posterior Beta con paramétros \(\alpha + s\) y \(\beta + f\),
curve(dbeta(x, a + s, b + f),
from = 0, to = 1,
xlab = "p", ylab = "Densidad", lty = 1, lwd = 4
)
curve(dbeta(x, s + 1, f + 1),
add = TRUE, lty = 2, lwd = 4
)
curve(dbeta(x, a, b),
add = TRUE, lty = 3, lwd = 4
)
legend(.7, 4, c("Previa", "Verosimilitud", "Posterior"),
lty = c(3, 2, 1), lwd = c(3, 3, 3)
)
(p_hat <- 11 / 27)[1] 0.4074074(p_posterior <- (a + s) / (a + s + b + f))[1] 0.3807744