set.seed(123)
theta_real <- 5
muestra <- matrix(rexp(n = 1000 * 3, rate = theta_real), ncol = 3)
suma_muestra <- apply(X = muestra, MARGIN = 1, FUN = sum)
theta_techo <- 3 / suma_muestra
hist(theta_techo - theta_real, breaks = 100)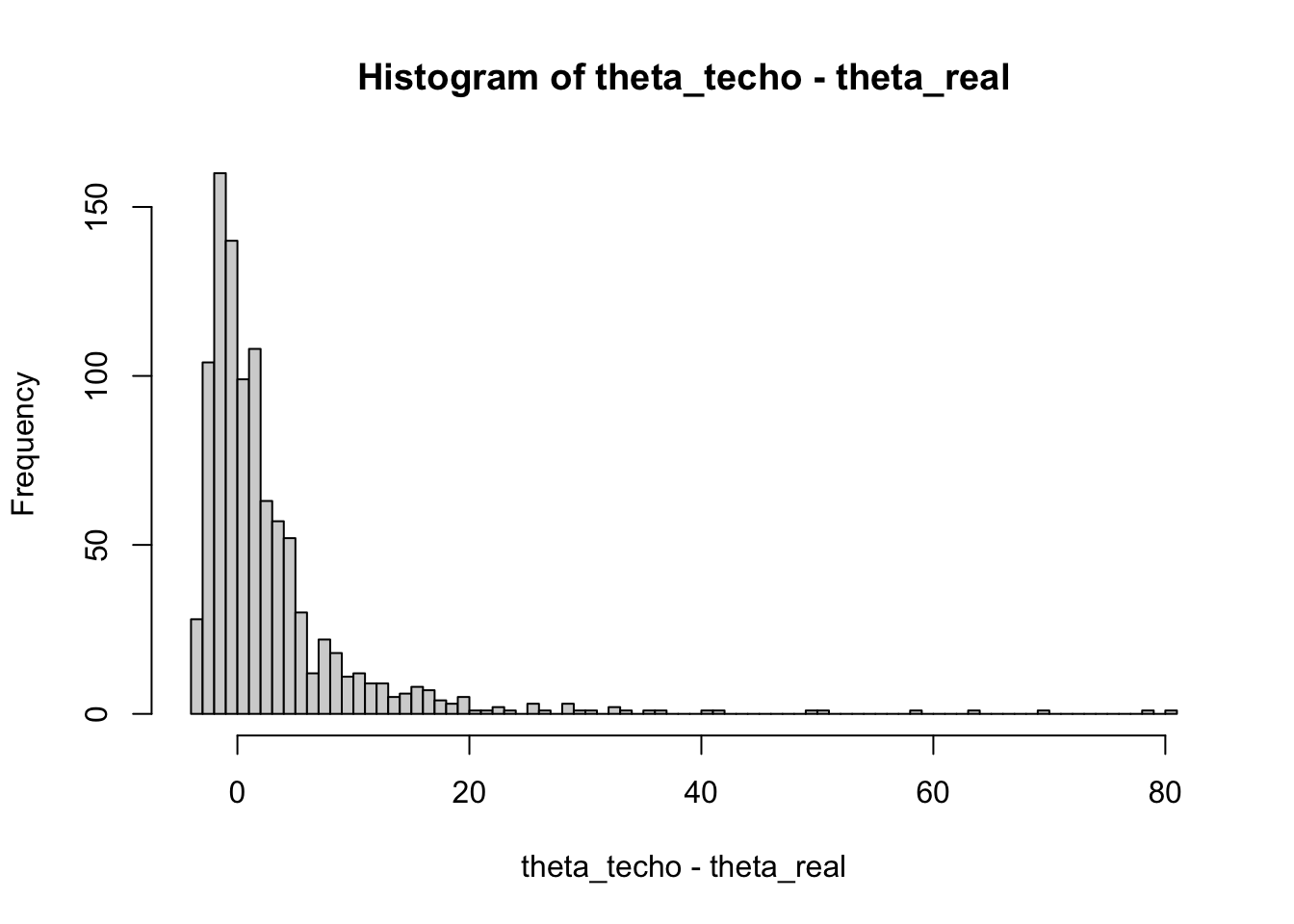
7 Estimación insesgada
Un estimador es una función que calcula una estimación o predicción de un parámetro desconocido en una distribución de probabilidad. En estadística, uno de los criterios importantes para evaluar la calidad de un estimador es si es insesgado.
Un estimador se considera insesgado si su valor esperado es igual al valor verdadero del parámetro que se está estimando. Esto se puede expresar matemáticamente como:
\[\begin{equation*} \mathbb E_{\theta}[\delta(x)] = g(\theta), \end{equation*}\]
donde \(\delta(x)\) es el estimador, \(g(\theta)\) es el parámetro que se está estimando y \(\mathbb E_{\theta}\) es el valor esperado bajo la distribución de probabilidad \(f(x\vert \theta)\). A la diferencia entre \(\mathbb{E}[\delta(x)]\) y \(g(\theta)\) se le conoce como el sesgo del estimador.
Ejemplo 7.1 Un ejemplo de un estimador insesgado es el promedio muestral \(\bar{X}_n\) cuando tenemos una muestra \(X_1,\dots,X_n\) de una distribución con media \(\mu\) cualquiera. En este caso: \[ \mathbb E[\bar X_n] = \dfrac 1n \sum_{i=1}^n\mathbb E(X_i) = \mu \]
Lo que significa que \(\bar X_n\) es estimador insesgado de la media poblacional \(\mu\).
Aunque la propiedades ser insesgado pareciera natural en los estimadores, no siempre tenemos esto.
Ejemplo 7.2 Considere una muestra \(X_1, X_2, X_3 \sim \mathrm{Exp}(\theta)\) con función de densidad \(f(x|\theta) = \theta e^{-\theta x}\).
De acuerdo a los ejemplos de capítulos pasados, el estimador de máxima verosimilitud de \(\theta\) es
\[\begin{equation*} \hat\theta = \dfrac{3}{T} = \dfrac{3}{\sum_{i=1}^{3}X_i}, \end{equation*}\]
Podemos preguntarnos si \(\hat\theta\) es un estimador insesgado de \(\theta\). Para responder a esta pregunta, realizamos una simulación en R para estimar el sesgo de \(\hat\theta\) utilizando valores generados aleatoriamente.
El histograma muestra la diferencia entre las estimaciones \(\hat{\theta}\) y el valor verdadero \(\theta\). Teóricamente, podemos calcular el sesgo de \(\hat{\theta}\) y encontramos que:
\[\begin{equation*} \mathbb E[\hat\theta] = \mathbb E\bigg[\dfrac 3T\bigg]= 3\mathbb E\bigg[\dfrac 1T\bigg], \quad T\sim \Gamma(3,\theta) \end{equation*}\]
Como \(\dfrac 1T \sim \text{Gamma Inversa}(3,\theta)\)1, se tiene que
1 La Gamma Inversa con parámetros \(\alpha\) y \(\beta\) tiene media \(\dfrac{\beta}{\alpha-1}.\)
\[\mathbb E\bigg[\dfrac 1T\bigg] = \dfrac{\theta}2 \implies \mathbb E[\hat \theta] =\dfrac{3\theta}2 \neq \theta\]
Por lo que \(\hat \theta\) es un estimador sesgado, con sesgo \[\text{sesgo}(\hat\theta) = \dfrac{3\theta}{2} -\theta = \dfrac \theta 2.\]
Si por ejemplo \(\theta=5\), entonces la diferencia debería ser aproximadamente \(\dfrac{5}{2}\approx 2.5\). Calculemos la diferencia promedio entre el estimador y el valor real:
mean(theta_techo - theta_real)[1] 2.804016Tomemos otro estimador, \(\theta_{U} = \dfrac {2\hat\theta}{3} = \dfrac 23 \cdot \dfrac{3}{T} = \dfrac 2T\). Entonces la esperanza de \(\theta_{U}\) es: \[\mathbb E[\theta_{U}] = \dfrac 23 \mathbb E(\hat\theta) =\dfrac 23 \cdot \dfrac 32 \theta = \theta.\]
Entonces \(\theta_{U}\) es un estimador insesgado.
Comprobemos que efectivamente \(\theta_{U}\) es insesgado:
theta_u <- 2 / suma_muestra
mean(theta_u - theta_real)[1] 0.2026772Con esto concluimos que el estimador de máxima verosimilitud no siempre es insesgado.
En un mundo ideal, nos gustaría tener estimadores insesgados pero que además tengan varianza pequeña, i.e., \(\text{Var}(\delta(x))\to 0\).
Ejemplo 7.3 Considere una muestra \(X_1, X_2, \dots, X_n \sim \mathrm{Exp}(\theta)\). De acuerdo a los ejemplos de capítulos pasados, el estimador de máxima verosimilitud de \(\theta\) es \(\frac{1}{\bar{X}_n}\)
- Generaremos múltiples muestras de una distribución exponencial con un \(\theta\) verdadero.
- Estimaremos \(\theta\) para cada muestra utilizando el MLE.
- Calcularemos el sesgo y la varianza de nuestras estimaciones.
- Graficaremos cómo varían el sesgo y la varianza con el tamaño de la muestra.
Viendo el gráfico queda la pregunta
Importante
¿Cómo controlar sesgo y varianza?
Para esto definamos el error cuadrático medio (MSE) de \(\delta(x)\) como \(\mathrm{MSE}(\delta(x)) = \mathbb E[(\delta(x)-\theta)^2]\).
Escribiendo la defnición de esta cantidad, podemos desagregar el MSE en dos partes:
\[\begin{align*} & \mathrm{MSE}(\hat{\theta}) \\ & = \mathbb E[(\hat{\theta}-\theta)^2] \\ & = \mathbb E[(\hat{\theta}-\mathbb E[\hat{\theta}] + \mathbb E[\hat{\theta}]-\theta)^2] \\ & = \mathbb E[(\hat{\theta}-\mathbb E[\hat{\theta}])^2] + \mathbb E[(\mathbb E[\hat{\theta}]-\theta)^2] + 2(\mathbb E[\hat{\theta}-\mathbb E[\hat{\theta}])(\mathbb E[\hat{\theta}]-\theta)] \\ & = \mathbb E[(\hat{\theta}-\mathbb E[\hat{\theta}])^2] + \mathbb E[(\mathbb E[\hat{\theta}]-\theta)^2] + 2\underbrace{(\mathbb E[\hat{\theta}]-\mathbb E[\hat{\theta}])}_{=0}(\mathbb E[\hat{\theta}]-\theta)] \\ & = \mathbb E[(\hat{\theta}-\mathbb E[\hat{\theta}])^2] + \mathbb E[(\mathbb E[\hat{\theta}]-\theta)^2] \\ & = \mathrm{Var}(\hat{\theta}) + \mathrm{Sesgo}^2(\hat{\theta}). \end{align*}\]
Si \(\delta\) tiene varianza finita, entonces definimos el error cuadrático medio (MSE) de \(\hat{\theta}\) como,
\[MSE_{\theta}(\hat{\theta}) =\text{Sesgo}^2(\hat{\theta}) + \text{Var}(\hat{\theta}).\]
Ejemplo 7.4 De acuerdo al primer ejemplo del capítulo, nos interesa comparar \(\hat\theta\) y \(U =\dfrac 2T\) en términos del MSE.
Dado que \(\text{Var}\left(\dfrac 1T\right) = \dfrac{\theta^2}4\)2, se tiene
2 Si \(X\sim\text{Gamma-Inversa}(\alpha, \beta)\) entonces \(\text{Var}(X)=\dfrac{\beta ^{2}}{(\alpha -1)^2(\alpha-2)}\).
- \(\mathrm{MSE}(\theta_{U}) = \text{Var}\left(\dfrac 2T\right) = 4\dfrac{\theta^2}4 = \theta^2\).
var(theta_u) + mean(theta_u - theta_real)^2[1] 28.17069- \(\mathrm{MSE}(\hat\theta) = (\text{Sesgo}(\hat\theta))^2+\text{Var}\left(\dfrac 3T\right) = \dfrac{\theta^2}{4}+\dfrac{9\theta^2}{4} = \dfrac{5\theta^2}{2}\).
var(theta_techo) + mean(theta_techo - theta_real)^2[1] 71.15413\(\theta_{U}\) es mejor estimador en términos de MSE que el \(\hat\theta\).
Observación. El estimado bayesiano es \(\theta_{Bayes} = \dfrac{4}{2+T}\) y este es un poco más eficiente que los otros dos.
theta_bayes <- 4 / (2 + suma_muestra)
var(theta_bayes) + mean(theta_bayes - theta_real)^2[1] 11.871937.1 Estimador insesgado de la varianza
Llegados a este punto, hemos estudiado con mucho detalle los estimadores de la media de una distribución. Hemos visto que en general estos estimadores son insesgados, suficientes, consistentes y eficientes. Sin embargo, en muchas ocasiones nos interesa encontrar un estimador insesgado de la varianza de una distribución. Para esto, consideremos una muestra \(X_1,\dots,X_n\) de una distribución \(F_{\theta}\) con varianza finita.
Definamos la varianza muestras como
\[\begin{equation*} s^2 = \dfrac{1}{n-1}\sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)^{2}. \end{equation*}\]
la cual se contrapone con la varianza poblacional
\[\begin{equation*} \hat{\sigma}^2 = \dfrac{1}{n}\sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)^{2}. \end{equation*}\]
Ambas son idénticas a excepción del denominador \(n\) o \(n-1\). Sin embargo, la diferencia fundamental reside en este teorema.
Teorema 7.1 Si \(X_1,\dots, X_n \sim F_{\theta}\) con varianza finita y \(g(\theta) = \text{Var}(X_1)\) entonces \[s^2 = \dfrac{1}{n-1}\sum(X_i-\bar X_n)^2\] es un estimador insesgado de \(\sigma^2\).
Ejemplo 7.5 Sean \(X_1,\dots,X_n \overset{i.i.d}{\sim}\text{Poisson}(\theta)\). \(\mathbb E(X_i) = \text{Var}(X_i) = \theta\). Algunos estimadores insesgados de \(\theta\) son:
\(\bar X_n\).
\(s^2\).
Si \(\alpha \in (0,1)\), \(T = \alpha\bar X_n + (1-\alpha)s^2\) también es un estimador insesgado.
muestra <- matrix(rpois(n = 1000 * 100, lambda = 2), nrow = 100)
media <- apply(muestra, 1, mean)
varianza <- apply(muestra, 1, var)
ambos <- apply(muestra, 1, function(x, alpha) {
alpha * mean(x) + (1 - alpha) * var(x)
}, alpha = 0.5)
hist(media)
hist(varianza)
hist(ambos)
Ejemplo 7.6 En caso de distribuciones normales, ¿Cuál estimador tiene menor MSE, \(\hat{\sigma}^2\) o \(s^2\)?
Defina \(T_c = c\sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)^{2}\). Si \(c = 1/n\), \(T_c = \hat\sigma^2\) y si \(c = 1/(n-1)\), \(T_c = s^2\). De esta manera,
\[\begin{align*} MSE_{\sigma^2}(T_c) & = \mathbb E\left[\left(T_c-\sigma^2\right)^2\right] \\ &=(\mathbb E(T_c)-\sigma^2)^2+\text{Var}(T_c). \end{align*}\]
\[\begin{align*} \mathbb E[T_c] & = c\mathbb E\left[\sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)^{2}\right] \\ & = c(n-1)\mathbb E\left[\dfrac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)^{2}}{n-1}\right] \\ & = c(n-1)\sigma^2. \end{align*}\]
\[\begin{align*} \text{Var}(T_c) & = c^2\text{Var}\left(\sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)^{2}\right) \\ & = c^2\text{Var}\Bigg(\sigma^2\underbrace{\sum_{i=1}^{n}\dfrac{\left(X_i-\bar X_n\right)}{\sigma^2}}_{\sim\chi^2_{n-1}}\Bigg) \\ & = 2c^2\sigma^4(n-1). \end{align*}\]
Entonces
\[\begin{align*} \mathrm{MSE}_{\sigma^2}(T_c) & = [c(n-1)\sigma^2-\sigma^2]^2+2c^2\sigma^4(n-1) \\ & =\left[\left[c(n-1)-1\right]^2+2c^2(n-1)\right]\sigma^4. \end{align*}\]
Optimizando,
\[\min_c \mathrm{MSE}(T_c) = \min_c[(n^2-1)c^2-2(n-1)c+1],\]
se encuentra que \(\hat c = \dfrac 1{n+1}\). Así, \(T_{\frac{1}{n+1}} = \dfrac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)^{2}}{n+1}\) es el mejor estimador de \(\sigma^2\) en el sentido de MSE. Aunque se puede demostrar que este estimador es inadmisible.
Ejercicio 7.1 Calcule el MSE de \(\hat\sigma^2\) y \(s^2\) y compare los resultados.
7.2 Información de Fisher
La Información de Fisher es una herramienta fundamental en inferencia estadística que nos permite cuantificar la cantidad de información que una muestra proporciona acerca de un parámetro desconocido.
Consideremos una variable aleatoria \(X\) con función de densidad \(f(x|\theta)\), donde \(\theta \in \Omega \subset \mathbb R\) es un parámetro fijo. Supongamos que \(X\) satisface los siguiente supuestos:
- Para cada \(x \in \mathcal X\) (espacio muestral de \(X\)), se tiene que \(f(x|\theta)> 0\) para todo \(\theta \in \Omega\). En otras palabras, la función \(f(x\mid\theta)\) depende de un parámetro \(\theta\) desconocido, pero el dominio de esta función no depende de \(\theta\).
- La función \(f(x|\theta)\) es dos veces diferenciable con respecto a \(\theta\).
- Es posible intercambiar el orden de la derivada y la integral en la siguiente expresión: \[\begin{equation*} \dfrac d{d\theta}\int_{\mathcal X}f(x|\theta)dx = \int_{\mathcal X}\dfrac d{d\theta}f(x|\theta)dx. \end{equation*}\]
Ejemplo 7.7 Si \(X\) sigue una distribución uniforme en el intervalo \([0,\theta]\), es decir, \(X\sim\text{Unif}[0,\theta]\), entonces \(f(x|\theta) = 1_{(0,\theta)}(x)\). En este caso, el primer supuesto no se cumple, ya que si \(x>\theta\), entonces \(f(x|\theta) = 0\). Esto significa que el dominio de la distribución no debe depender de \(\theta\).
La siguiente función será clave para definir la información de Fisher.
Definición 7.1 Definimos la función Score como: \[\lambda(x|\theta)=\ln f(x|\theta)\] Sus derivadas son: \[\lambda^{\prime}(x|\theta) = \dfrac \partial{\partial \theta}\ln f(x|\theta)\] \[\lambda^{\prime\prime}(x|\theta) = \dfrac {\partial^2}{\partial \theta^2}\ln f(x|\theta)\]
Definición 7.2 Si \(X\) y \(f(x|\theta)\) cumplen con los supuestos mencionados, la información de Fisher de \(X\) está dada por: \[I(\theta) =\mathbb E[(\lambda'(x|\theta))^2]\] Donde la esperanza es una integral o suma, dependiendo de si \(X\) es continua o discreta. Por ejemplo, para una variable continua: \[I(\theta)=\int_{\mathcal{X}}\left[\lambda^{\prime}(x \mid \theta)\right]^{2} f(x \mid \theta) d x\]
Teorema 7.2 Bajo las condiciones anteriores, y suponiendo que las dos derivadas de \(\int_{\mathcal X}f(x|\theta)dx\) con respecto a \(\theta\) (Supuesto 3) se pueden calcular al intercambiar el orden de integración y derivación. Entonces
\[ I(\theta) = -\mathbb E_{\theta}[\lambda''(x|\theta)] = \text{Var}[\lambda'(x|\theta)]. \]
La Información de Fisher es una herramienta esencial en inferencia estadística que nos permite cuantificar la cantidad de información que una muestra proporciona acerca de un parámetro desconocido.
RESULTADO IMPORTANTE
Dada la función score \(\lambda(x\vert \theta) = \ln f(x\vert \theta)\), se tienen los siguientes resultados:
- \(\lambda^{\prime}(x\vert \theta)\) es una variable aleatoria.
- \(\mathbb{E}[\lambda^{\prime}(x\vert \theta)] =0\).
- La varianza de \(\lambda^{\prime}(x\vert \theta)\) es igual a la información de Fisher: \[\begin{equation*} \mathrm{Var}[\lambda^{\prime}(x\vert \theta)] = I(\theta) = - \mathbb E[\lambda^{\prime\prime}(x|\theta). \end{equation*}\]
Ejemplo 7.8 Si \(X\sim \text{Bernoulli}(p)\), entonces:
- La función de densidad es \(f(x|p) = p^x(1-p)^{1-x}\) para \(x=0,1\), la cual satisface el supuesto 1.
- Se puede comprobar que satisfacen el supuesto 3, es decir, \(\int_\mathcal{X} \frac{d}{dp}f(x|p)dx = \frac{d}{dp}\int_\mathcal{X} f(x|p)dx\).
- La función score es \(\lambda(x|p) = x\ln p + (1-x)\ln(1-p)\).
- Las derivadas de la función score son:
- \(\lambda^{\prime}(x|p) = \dfrac xp-\dfrac{1-x}{1-p}\).
- \(\lambda^{\prime\prime}(x|p) = -\dfrac x{p^2}-\dfrac{1-x}{(1-p)^2}\).
La información de Fisher para esta distribución es:
\[I(p) = \mathbb E\bigg[\dfrac xp + \dfrac{1-x}{(1-p)^2}\bigg] = \dfrac p{p^2}+\dfrac{1-p}{(1-p)^2} = \dfrac 1{p(1-p)} = \dfrac 1{\text{Var}(X)}.\]
Ejemplo 7.9 Para \(X\sim N(\mu,\sigma^2)\) con \(\mu\) desconocida y \(\sigma^2\) conocida:
- La función de densidad es: \[f(x|\mu) = \dfrac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\dfrac 1{2\sigma^2}(x-\mu)^2\right)\].
- El tercer supuesto se cumple ya que \[\begin{align*} \dfrac d{du}\int_{\mathbb R} f(x|\mu)dx & = \int_{\mathbb R}f'(x|\mu)dx \\ & = \int_{\mathbb R} -\dfrac 1{\sqrt{2\pi\sigma^2}}\dfrac {2(x-\mu)^2}{2\sigma^2} dx \\ & = -\dfrac 1\sigma \underbrace{\int_{\mathbb R}\dfrac{u}{\sqrt{2\pi}}e^{-\frac{u}2}du}_{\mathbb E[N(0,1)]} = 0 \quad \text{usando el cambio de variable } \dfrac{x-\mu}\sigma \end{align*}\]
Entonces:
- La función score es \(\lambda(x|\mu) = \dfrac 12 \ln (2\pi\sigma^2)-\dfrac 1{2\sigma^2}(x-\mu)^2\).
- Las derivadas de la función score son:
- \(\lambda'(x\mid\mu) = \dfrac{x-\mu}{\sigma^2}\).
- \(\lambda''(x\mid\mu) = -\dfrac 1{\sigma^2}\).
La información de Fisher para esta distribución es: \[I(\mu) = -\mathbb E[\lambda^{\prime\prime}(x\mid\mu)] = \dfrac{1}{\text{Var}(X)}\]
Estos ejemplos fueron estimados usando solo un dato \(X\) de la distribución correspondiente. Sin embargo, este resultado se puede extender a una muestra \(X_1,\dots,X_n\)..
Definición 7.3 Suponga que \(X = (X_1,\dots,X_n)\) muestra de \(f(x|\theta)\) donde \(f\) satisface las condiciones anteriores. Defina \(\lambda_n(x\mid\theta) = \ln f_n(x|\theta)\). La información de Fisher de \(X\) es
\[I_n(\theta) = \mathbb E[(\lambda_{n}^{\prime}(x|\theta))^2] = - \mathbb E[\lambda^{\prime\prime}_n(x|\theta)].\]
Observación. La fórmula anterior, no es tan útil como quisieramos. En particular observe que \[\lambda_n(x|\theta) = \ln f_n(x|\theta) = \sum_{i=1}^{n} \lambda(X_i|\theta)\] lo que implica que \[\lambda^{\prime\prime}_n(x|\theta) = \sum_{i=1}^n\lambda(X_i|\theta).\] De esta forma, \[I_n(\theta) = -\mathbb E[\lambda^{\prime\prime}(x|\theta)] = - \sum_{i=1}^n\mathbb E[\lambda^{\prime\prime}(X_i|\theta)] = nI(\theta).\]
Ejemplo 7.10 Suponga que una compañía quiere conocer como se comportan sus clientes en sus tiendas. Hay dos propuestas para este modelo
Un modelo Poisson de parámetro \(t\theta\) (\(t\) es cualquier valor) para determinar la tasa promedio de llegada de clientes. \(Y\sim \text{Poisson}(\theta t)\).
Un modelo donde cada cliente es una v.a. exponencial con tasa de llegada \(\theta\) y al final se sumará todas las variables para obtener una \(\mathrm{Gamma}(n,\theta)\). \(X\sim \sum_{i=1}^{n}\text{Exp}(\theta) = \Gamma(n,\theta)\)
El tiempo de llegada de cada cliente es independiente.
¿Cuál variable contiene más información de \(\theta\) \(X\) o \(Y\)?
Solución:
Caso de la variable aleatoria \(Y\)
Acá tenemos que:
\(f(y|\theta) = e^{-t\theta}\dfrac{(t\theta)^y}{y!}\).
\(\lambda(y|\theta) = t\theta + y\ln (t\theta) - \ln y!\).
\(\lambda^{\prime}(y|\theta) = -t+\dfrac{ty}{t\theta}.\)
\(\lambda^{\prime\prime}(y|\theta) = -\dfrac y{\theta^2}\).
Entonces, \[I_Y(\theta) =-\mathbb E[ \lambda^{\prime\prime}(y|\theta)] = \dfrac{\mathbb E[Y]}{\theta^2} = \dfrac{t}\theta.\]
Caso de la variable aleatoria \(X\)
Para \(X\) queda como ejercicio, verificar que \(I_X(\theta) = \dfrac n{\theta^2}\).
Ambas variables tienen la misma información si
\[I_Y(\theta) = I_X(\theta) \implies \dfrac t\theta = \dfrac n{\theta^2} \implies n = \dfrac{\theta^2 t}{\theta } = t\theta.\]
A partir de este ejercicio vamos a hacer un pequeño ejemplo de simulación.
Suponga que \(t\) es el tiempo que se quiere medir la cantidad de clientes (minutos), \(\theta\) es la cantidad de clientes por minuto y \(n\) es el número de clientes que entran.
theta <- 5
tiempo <- 20 # t = tiempo
clientes <- tiempo * theta # n = clientes
muestra_y <- rpois(n = 1000, lambda = tiempo * theta)
muestra_x <- rgamma(n = 1000, shape = clientes, rate = theta)Según lo estimado ambas informaciones de Fisher debería dar aproximadamente igualdad.
Para \(Y\) tenemos que
mean(muestra_y / theta^2)[1] 4.01772Para \(X\) por otro lado la información de Fisher es constante (¿Por qué?)
clientes / theta^2[1] 4Entonces bajo este criterio, ambas variables contienen la misma información, aunque modelen el problema desde ópticas diferentes.
El proceso \(Y\) (Poisson) modela cuántas personas en total entran a la tienda en 20 minutos, asumiendo una tasa de entrada de 5 personas por minuto.
hist(muestra_y)
El proceso \(X\) (Gamma) modela cuánto tiempo se debe esperar para que 100 personas entren a la tienda, asumiendo una tasa de entrada de 5 por minuto.
hist(muestra_x)
Ejercicio 7.2 Basado en los valores de la simulación, proponga dos valores de \(t\) para que
- \(X\) tenga más información que \(Y\).
- \(Y\) tenga más información que \(X\).
7.3 Desigualdad de Cramer-Rao
Teorema 7.3 Si \(X = (X_1,\dots, X_n)\) muestra de \(f(x|\theta)\). Todos los supuestos anteriores son válidos para \(f\). Sea \(T = r(X)\) un estadístico con varianza finita. Sea \(m(\theta) = \mathbb E_{\theta}[T]\) y asuma que \(m\) es diferenciable. Entonces: \[\text{Var}_\theta(T)\geq \dfrac{[m'(\theta)]^2}{I_n(\theta)} =\dfrac{[m'(\theta)]^2}{nI(\theta)} .\]
La igualdad se da si y solo si existen funciones \(u(\theta)\) y \(v(\theta)\) que solo dependen de \(\theta\) tales que \[T = u(\theta)\lambda_n'(x|\theta) + v(\theta).\]
Caso particular
Si \(T\) es un estimador insesgado de \(\theta\), entonces \(\text{Var}_\theta(T)\geq \dfrac{1 }{I_n(\theta)}\).
Ejemplo 7.11 Sea \(X_1,\dots, X_n \sim \text{Exp}(\beta)\), \(n>2\).
\(f(x|\beta) = \beta e^{-\beta x}\), \(x>0\).
\(\lambda(x|\beta) = \ln f(x|\beta) = \ln \beta -\beta x\).
\(\lambda^{\prime}(x|\beta) = \dfrac 1\beta -x.\)
\(\lambda'' = -\dfrac 1{\beta^2}\).
Vea que \[1 = \int_{0}^\infty \beta e^{-\beta x}dx = \lim_{u\to \infty}F(u) = \lim_{u\to \infty}[1-e^{-\beta u}]\]
y el supuesto 3 se puede verificar por la diferenciabilidad de \(1-e^{-\beta u}\).
Así, \[I(\beta) = -\mathbb E[\lambda^{\prime\prime}(x|\beta)] = \dfrac 1{\beta^2}, \quad I_n(\beta) = \dfrac{n}{\beta^2}.\]
Por ejemplo generemos una secuencia de valores de \(\beta\) de 1 hasta 5 para observar el comportamiento de su información de Fisher.
beta <- seq(1, 5, length.out = 100)
n <- 100
lista_muestras <- lapply(
X = beta,
FUN = function(b) {
matrix(rexp(n = n * 500, rate = b), nrow = 500)
}
)
plot(beta, n / beta^2)
Considere el estadístico \(T = \dfrac{n-1}{\sum_{i=1}^n X_i}\) es un estimador insesgado de \(\beta\). La varianza de \(T\) es \(\dfrac{\beta^2}{n-2}\).
La cota de Cramer Rao, si \(T\) es insesgado, es
\[\dfrac 1{I_n(\beta)} = \dfrac{\beta^2}{n},\]
por lo que \(T\) no satisface la cota de Cramer Rao.
Este comportamiento podemos observarlo con nuestro ejemplo numérico.
estimador1 <- sapply(
X = lista_muestras,
FUN = function(x) {
apply(x, 1, function(xx) (n - 1) / sum(xx))
}
)
plot(beta, apply(X = estimador1, MARGIN = 2, FUN = mean))
plot(beta, apply(X = estimador1, MARGIN = 2, FUN = var))
lines(beta, beta^2 / n, col = "blue")
lines(beta, beta^2 / (n - 2), col = "red")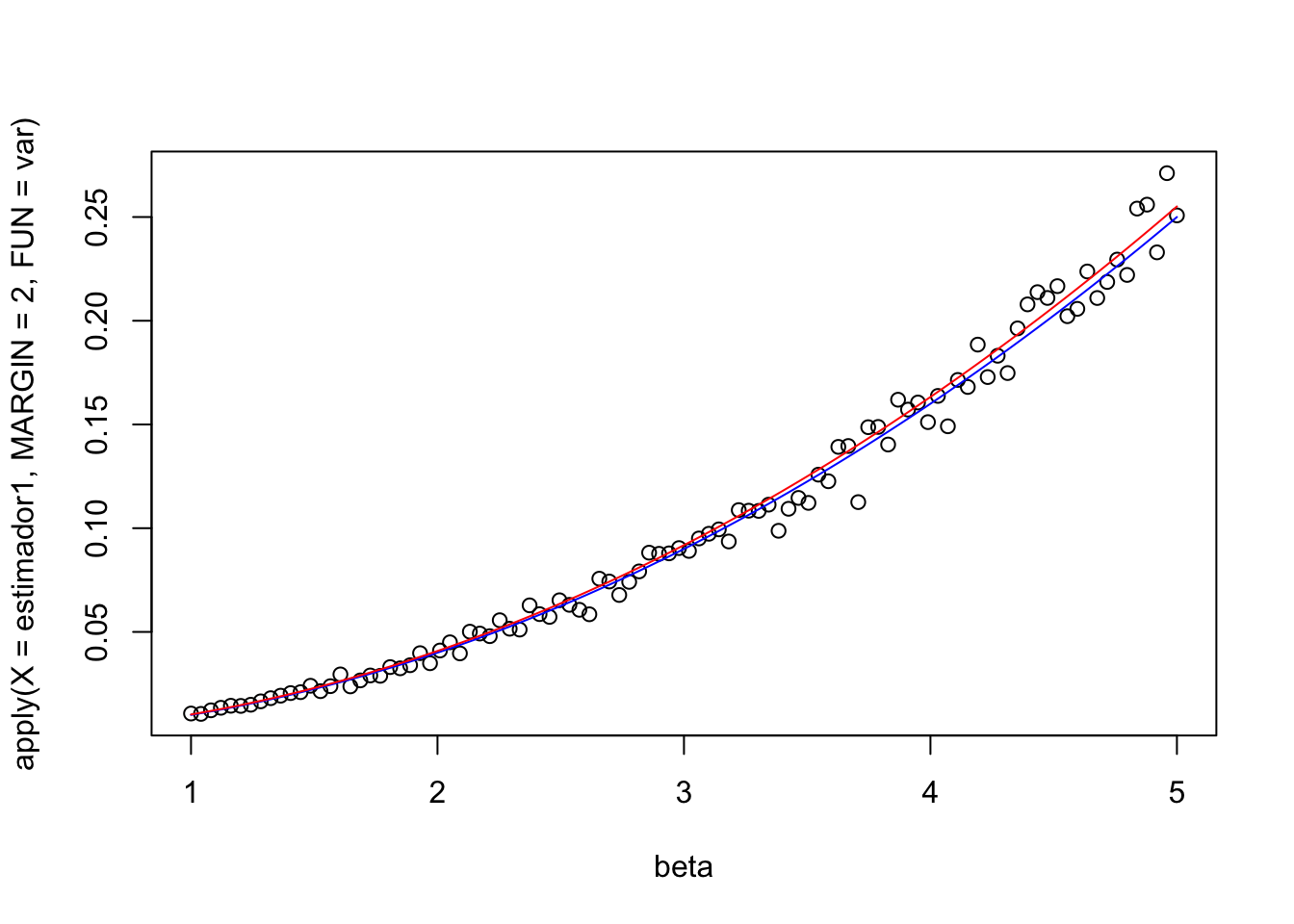
Ahora, estime \(\theta = \dfrac 1\beta = m(\beta)\). Un estimador insesgado de \(\theta\) es \(T =\bar X_n\):
\[\mathbb E[\bar X_n] = \mathbb E [X_1] = \dfrac 1\beta = \theta, \quad \text{Var}(\bar X_n) = \dfrac{\text{Var}(\bar X_1) }{n} = \dfrac 1{n\beta^2}.\]
La cota de Cramer es
\[\dfrac{(m'(\beta))^2}{I_n(\beta)} = \dfrac{(-1/\beta^2)^2}{n/\beta^2} = \dfrac{\beta^2}{n\beta^4} = \dfrac{1}{n\beta^2}.\]
\(\bar X_n\) satisface la cota de Cramer-Rao y además \[\lambda^{\prime}(X|\beta) = \dfrac n\beta - n\bar X_n =\dfrac n\beta - nT \implies T = \underbrace{-\dfrac 1n}_{u(\beta)}\lambda_n'(X|\beta)+ \underbrace{\dfrac 1\beta}_{v(\beta)}. \]
estimador2 <- sapply(
X = lista_muestras,
FUN = function(x) {
apply(x, 1, function(xx) mean(xx))
}
)
plot(1 / beta, apply(X = estimador2, MARGIN = 2, FUN = mean))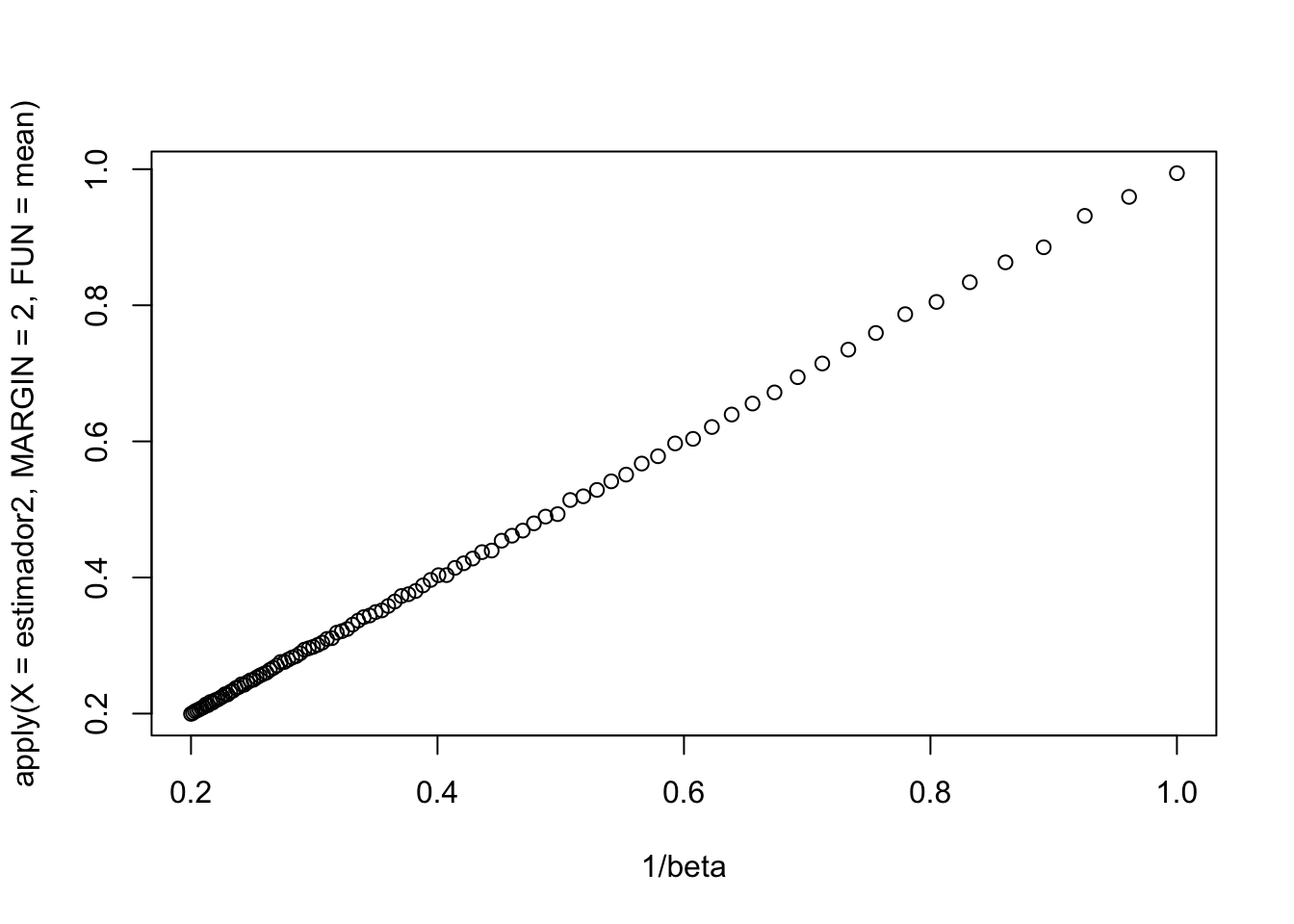
plot(beta, apply(X = estimador2, MARGIN = 2, FUN = var))
lines(beta, 1 / (n * beta^2), col = "blue")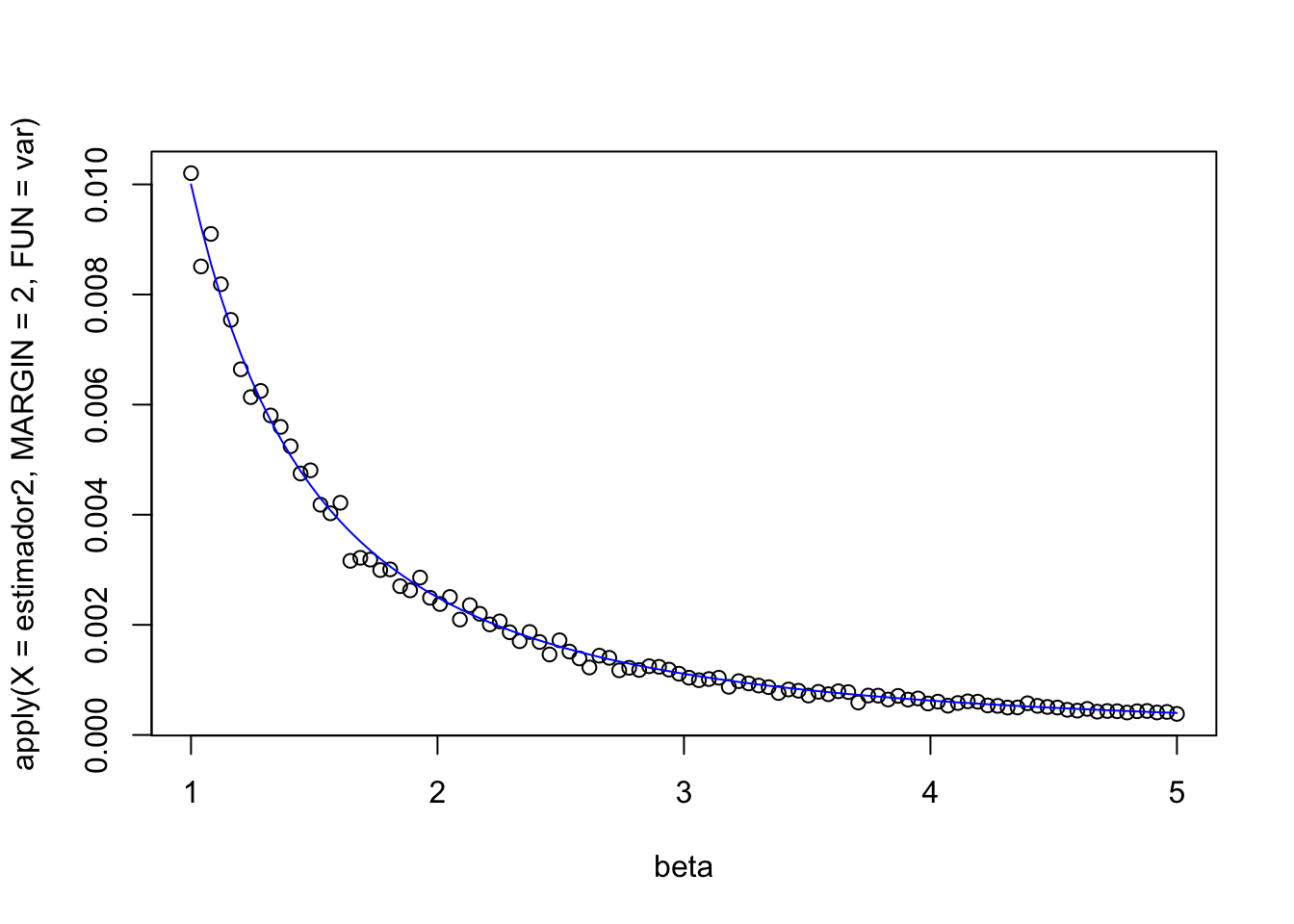
7.4 Estimadores eficientes
Definición 7.4 sea \(T\) es un estimador eficiente de su esperanza \(m(\theta)\) si su varianza es la cota de Cramer-Rao.
Ejemplo 7.12 Sea \(X_1,\dots, X_n\sim \text{Poisson}(\theta)\). \(\bar X_n\) es un estimador eficiente.
Verosimilitud: \(f_n(X|\theta) = e ^{n\theta}\dfrac{\theta^{n\bar X_n}}{\prod X_i!}\).
\(\lambda_n(X|\theta) = -n\theta + n\bar X_n \ln \theta - \ln \prod X_i!\).
\(\lambda'_n(X|\theta) = -n+\dfrac{c\bar X_n}{\theta}\).
\(\lambda_n''(X) = -\dfrac{n\bar X_n}{\theta^2}\).
Entonces \[\dfrac{n}{\theta^2}\mathbb E[\bar X_n] = \dfrac n{\theta}.\]
La cota de Cramer-Rao es \(\dfrac \theta n\), pero \[\text{Var}(\bar X_n) = \dfrac{\text{Var}(X_1)}{m} = \dfrac \theta n.\] Por lo que \(\bar X_n\) es eficiente.
Los otros candidatos para estimar \(\theta\) \[s^2=\dfrac 1{n-1}\sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)^{2} = \dfrac 1{n-1}\sum (X_i-\bar X_n)^2,\] y \[\alpha \bar X_n + (1-\alpha)\hat\sigma^2_1\] no son lineales con respecto a \(\lambda^{\prime}(X|\theta)\) por lo que tienen mayor varianza que \(\bar X_n\).
7.5 Comportamiento asintótico del MLE
Teorema 7.4 Teorema. Bajo las condiciones anteriores y si \(T\) es un estimador eficiente de \(m'(\theta)\) y \(m'(\theta) \neq 0\), entonces \[\dfrac 1{\sqrt{\sigma^2_{\mathrm{CR}}}}[T-m(\theta)]\xrightarrow{d}N(0,1)\]
donde \(\sigma^2_{\mathrm{CR}}\) es la varianza de la cota de Cramer-Rao.
Teorema 7.5 Recuerde que el MLE \(\hat \theta_n\) se obtiene al resolver la ecuación \(\lambda^{\prime}(x|\theta) = 0\). Además, \(\lambda^{\prime\prime}(x|\theta)\) y \(\lambda'''(x|\theta)\) existen y las condiciones anteriores son ciertas. Entonces, la distribución asintótica de \(\hat\theta_n\) cumple que: \[[nI(\theta)]^{1/2}(\hat\theta-\theta) \to N(0,1).\]
Ejemplo 7.13 Sea \(X_1,\dots, X_n \sim N(0,\sigma^2)\), \(\sigma\) desconocida. \(\hat\sigma = \bigg[\dfrac 1n \sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)^{2}\bigg]^{1/2}\) es MLE de \(\sigma\) y \(I(\sigma) = \dfrac 2{\sigma^2}\). Usando el teorema,
\[ \sqrt{\dfrac{2n}{\sigma^2}} (\hat{\sigma} - \sigma) \underset{n\to\infty}{\to} N\left(0,1\right). \] O lo que es equivalente a \[\hat{\sigma} \underset{n\to\infty}{\to} N\left(\sigma,\dfrac{\sigma^2}{2n}\right).\]
7.6 Estimador MLE en el caso bayesiano
Desde la perspectiva bayesiana, el Estimador de Máxima Verosimilitud \(\theta_n\) tiene propiedades interesantes al hacer inferencias sobre un parámetro \(\theta\).
Propiedad General
Supongamos que la distribución a priori de \(\theta\) está representada por una función de densidad de probabilidad (p.d.f.) positiva y diferenciable en un intervalo determinado. Si el tamaño de la muestra \(n\) es grande y se cumplen ciertas condiciones de regularidad (similares a las necesarias para asegurar la normalidad asintótica de \(\theta_n\)), entonces la distribución a posteriori de \(\theta\), después de observar los valores \(X_1, \dots, X_n\), será aproximadamente normal con media \(\theta_n\) y varianza \(1/[nI (\theta_n)]\).