Código
x <- rexp(n = 100, rate = 1)
n <- length(x)
y <- sum(x)
theta <- seq(0.5, 1.5, length.out = 1000)5 Estimación por máxima verosimilitud
En el capítulo anterior, nos enfocamos en construir una distribución posterior a partir de una distribución previa. Sin embargo, surge una pregunta:
¿Es posible estimar la distribución posterior sin una densidad previa?
Para responderla, primero debemos revisar algunas definiciones relacionadas con la muestra y la independencia condicional al valor de un parámetro.
Definición 5.1 (Función de verosimilitud) Dada una muestra \(X_1, \dots , X_n\) que son variables aleatorias independientes e idénticamente distribuidas (i.i.d.) con distribución \(f(X\mid \theta)\) y un \(\theta\) fijo, la función de verosimilitud se define como:
\[ f_n (X\mid \theta) = \prod_{i=1}^n f(X_i\mid \theta) = L(\theta\mid X). \]
Si consideramos dos valores posibles del parámetro, \(\theta_1\) y \(\theta_2\), y evaluamos la función de verosimilitud para cada uno de ellos, obtenemos: \[\begin{align*} f_n(X\mid \theta_1) &= \prod_{i=1}^n f(X_i\mid \theta_1) = L(\theta_1\mid X) \\ f_n(X\mid \theta_2) &= \prod_{i=1}^n f(X_i\mid \theta_2) = L(\theta_2\mid X) \end{align*}\]
El principio de verosimilitud establece que si \(f_n(X\mid \theta_1)>f_n(X\mid \theta_2)\), entonces \(L(\theta_1\mid X)>L(\theta_2\mid X)\).
Observación. Es más verosímil (realista) que el verdadero valor del parámetro sea \(\theta_1\) que \(\theta_2\) dada la muestra observada.
Definición 5.2 (Estimador de máxima verosimilitud (MLE)) Para cada observación \(x\) en el espacio muestral \(X\), si existe un estimador \(\delta(x)\) de \(\theta\) que maximiza la función de verosimilitud \(f_n(x\mid \theta)\), entonces a \(\delta(x)\) se le denomina estimador de máxima verosimilitud (MLE).
Ejemplo 5.1 Consideremos una muestra \(X_1,\dots, X_n\) con distribución exponencial \(\text{Exp}(\theta)\), donde la función de densidad es \(\frac{1}{\theta} e^{-\frac{x}{\theta}}\) si \(x>0\). Estamos interesados en estimar \(\theta\).
La función de verosimilitud es:
\[\begin{equation*} f_n(X\mid \theta) = \frac{1}{\theta^n}\exp\left({-\frac{\sum_{i=1}^n x_i}{\theta}}\right) = \theta^{-n} \exp\left({-\frac{y}{\theta}}\right) . \end{equation*}\]
Donde \(y = \sum_{i=1}^n x_i\).
La log-verosimilitud es una transformación monótona creciente de la función de verosimilitud y se define como:
\[\begin{equation*} \ell(\theta\mid X) = \ln f_n(X\mid \theta) = -n\ln \theta - \frac{y}{\theta}. \end{equation*}\]
Para encontrar el MLE de \(\theta\), derivamos la log-verosimilitud con respecto a \(\theta\) y resolvemos para \(\theta\):
\[\begin{align*} \frac{\partial}{\partial\theta} \ell(\theta\mid X) &= \frac{\partial}{\partial\theta} \left[ -n\ln \theta - \frac{y}{\theta} \right] = -\frac{n}{\theta} + \frac{y}{\theta^2} = 0 \\ \implies \frac{1}{\theta}\left(-n + \frac{y}{\theta}\right) &= 0 \\ \implies \hat\theta = \frac{y}{n} &= \bar{X}_n. \end{align*}\]
Para verificar que \(\hat\theta\) es un máximo, derivamos la log-verosimilitud con respecto a \(\theta\) dos veces y evaluamos en \(\theta = \hat\theta\):
\[\begin{align*} \frac{\partial^2}{\partial\theta^2} \ell(\theta\mid X) &= \left. \frac{n}{\theta^2} - \frac{2y}{\theta^3}\right|_{\theta=\frac{y}{n}} \\ &= \frac{n}{\left(\frac{y}{n}\right)^2} - \frac{2y}{\left(\frac{y}{n}\right)^3} \\ &= \frac{n^3}{y^2} - \frac{2n^3}{y^2} \\ &= -\frac{n^3}{y^2} < 0. \end{align*}\]
Por lo tanto \(\hat\theta = \bar{X}_n\) es el MLE de \(\theta\).
Ahora generemos 100 valores con una distribución exponencial con parámetro \(\theta=1\) y grafiquemos la función de verosimilitud y la log-verosimilitud:
Código
ggplot(
data.frame(
theta = theta,
L = theta^(-n) * exp(-y / theta)
),
aes(x = theta, y = L)
) +
geom_line(linewidth = 2) +
geom_vline(aes(xintercept = mean(x)), linewidth = 2, color = "red") +
cowplot::theme_cowplot() +
labs(
title = "Verosimilitud con la media de x",
x = "Theta",
y = "Verosimilitud"
)
Código
ggplot(
data.frame(
theta = theta,
l = -n * log(theta) - y / theta
),
aes(x = theta, y = l)
) +
geom_line(linewidth = 2) +
geom_vline(aes(xintercept = mean(x)), linewidth = 2, color = "red") +
cowplot::theme_cowplot() +
labs(
title = "Log-verosimilitud con la media de x",
x = "Theta",
y = "Verosimilitud"
)
Ejemplo 5.2 Suponga que se está haciendo pruebas RT-PCR para detectar el virus SARS-CoV-2. La prueba es 90% confiable en el siguiente sentido:
- Si la persona es positiva, entonces la probabilidad que una persona sea efectivamente positiva es 0.9. Si la persona es negativa, entonces la prueba dirá con probabilidad 0.1 que positiva.
- El mismo razonamiento aplica si una persona es negativa. La prueba dirá con 0.9 probabilidad que es negativa; mientras que si es realmente es positiva dirá con 0.1 probabilidad que es negativa.
En este caso nuestra variable aleatoria es \(\text{Bernoulli}(\theta)\),donde el espacio total parametrico consiste de \(\theta \in \{0.9,0.1\}\). En este ejemplo \(0.1\) significa negativo y \(0.9\) significa positivo.
Nuestra muestra tendria la siguiente forma:
\[x = \begin{cases}1 & \text{si la prueba es positiva}\\0& \text{si no}\end{cases}\]
Resumiento el comportamiento de la prueba, tendríamos estas funciones de densidad
Si \(x=1\), entonces \(f(1\mid\theta) = \mathbb{P}(\theta \mid x=1)= \begin{cases}0.1 & \text{si }\theta = 0.1\\0.9& \text{si }\theta = 0.9\end{cases}\).
Si \(x=0\), entonces \(f(0\mid\theta) = \mathbb{P}(\theta \mid x=0) = \begin{cases}0.9 & \text{si }\theta = 0.1\\0.1& \text{si }\theta = 0.9\end{cases}\).
Veamos este gráfico que explica lo que está sucediendo:
graph TB
inicio(Inicio) --> prueba("Resultado de la Prueba")
prueba --> theta09("Positiva (x=1)" )
prueba --> theta01("Negativa (x=0)")
theta01 --> p01a("P(θ=0.1|x=0) = 0.9"):::max
theta01 --> p01b("(P(θ=0.9|x=0) = 0.1)")
theta09 --> p09a("P(θ=0.1|x=1) = 0.1")
theta09 --> p09b("P(θ=0.9|x=1) = 0.9"):::max
classDef max fill:#ff9999,color:#000,stroke-width:4px;
%% classDef default fill:#f9f,stroke:#333,stroke-width:4px;
%% classDef theta fill:#bbf,stroke:#333,stroke-width:4px;
%% class prueba,theta01,theta09 theta;
Entonces los cuadros marcados en rojos, indican donde se maximiza la probabilidad para este ejemplo. Por lo tanto el MLE corresponde a \[\hat\theta = \begin{cases}0.1 & \text{si }x= 0\\0.9& \text{si }x= 1\end{cases}\]
Código
theta <- c(0.1, 0.9)
## Define f(0|theta)
f_x0 <- c(0.9, 0.1)
## Define f(1|theta)
f_x1 <- c(0.1, 0.9)
df <- data.frame(
theta = rep(theta, 2),
likelihood = c(f_x0, f_x1),
x = factor(rep(0:1, each = 2))
)
# Gráfico
ggplot(df, aes(x = as.factor(theta), y = likelihood, fill = x)) +
geom_bar(stat = "identity", position = "dodge") +
labs(
title = "Función de verosimilitud para diferentes valores de x",
x = expression(theta),
y = "Verosimilitud",
fill = "Valor de x"
) +
theme_minimal() +
scale_fill_manual(values = c("blue", "red"), labels = c("x = 0", "x = 1"))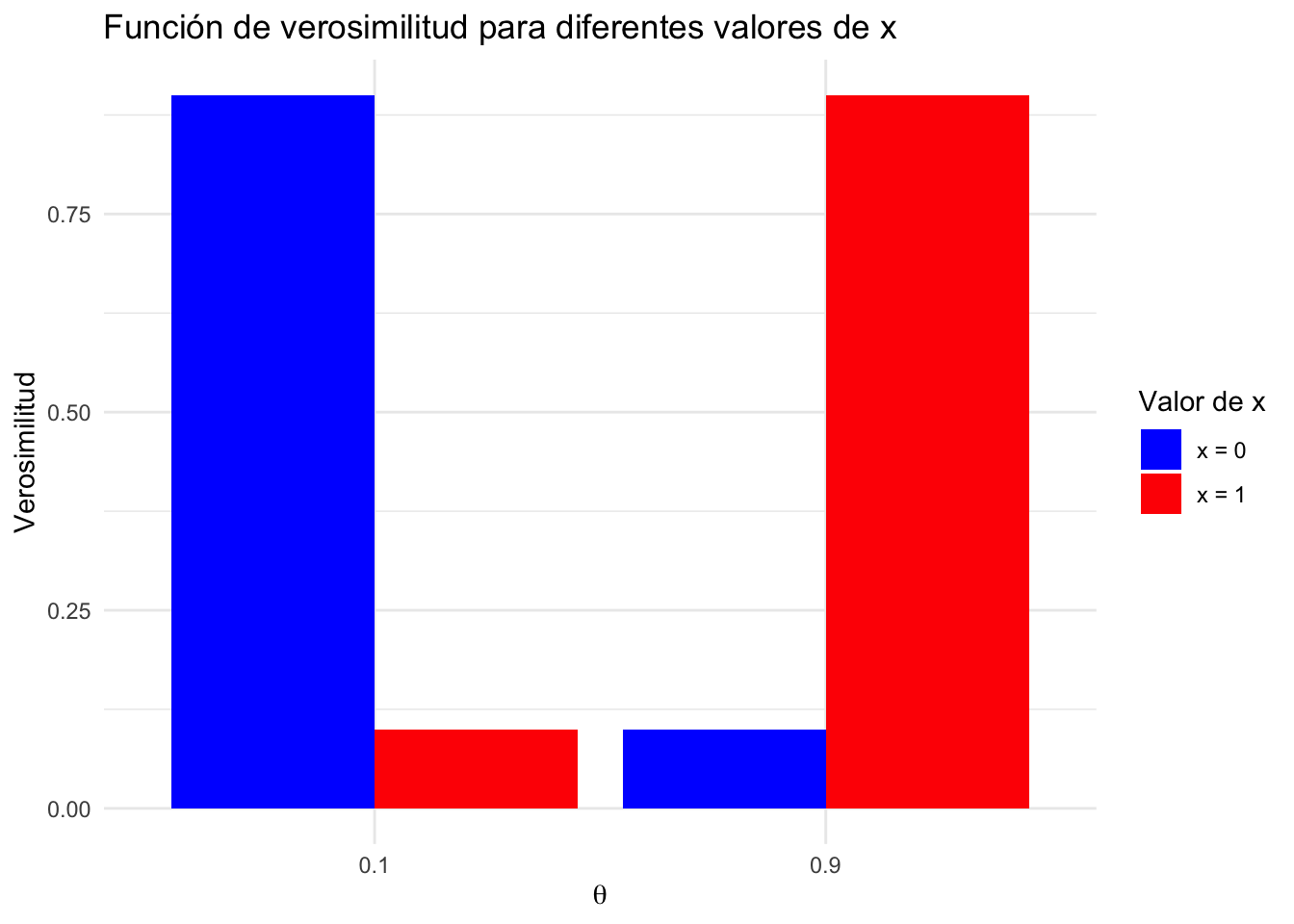
Ejemplo 5.3 (Caso 1: Varianza conocida) Consideremos una muestra \(X_1,\dots, X_n\) que sigue una distribución normal \(N(\mu,\sigma^2)\) con \(\sigma^2\) conocida. Estamos interesados en estimar el parámetro \(\mu\).
La función de verosimilitud para esta muestra es:
\[\begin{equation*} f_n(X\mid \mu) = \prod_{i=1}^n f(X_i\mid \mu) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right) = (2\pi\sigma^2)^{-n/2}\exp\left(-\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2\right). \end{equation*}\]
La log-verosimilitud es:
\[\begin{equation*} \ell(\mu\mid X) = \ln f_n(X\mid \mu) = -\frac{n}{2}\ln(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2. \end{equation*}\]
Para encontrar el estimador de máxima verosimilitud (MLE) de \(\mu\), derivamos la log-verosimilitud con respecto a \(\mu\) y resolvemos para \(\mu\):
\[\begin{align*} \frac{\partial}{\partial\mu} \ell(\mu\mid X) &= \frac{\partial}{\partial\mu} \left[ -\frac{n}{2}\ln(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^n(X_i-\mu)^2 \right] \\ &= \frac{1}{\sigma^2}\sum_{i=1}^n(X_i-\mu) = 0 \\ \implies \sum_{i=1}^n(X_i-\mu) &= 0 \\ \implies \sum_{i=1}^n X_i - n\mu &= 0 \\ \implies \hat\mu = \frac{1}{n}\sum_{i=1}^n X_i &= \bar{X}_n. \end{align*}\]
Dado que la función es cuadrática en \(\mu\), tiene un único máximo. Por lo tanto, el MLE de \(\mu\) es:
\[\begin{equation*} \hat\mu = \bar{X}_n. \end{equation*}\]
Ejemplo 5.4 (Caso 2: Varianza desconocida) Si consideramos una muestra \(X_1,\dots, X_n\) que sigue una distribución normal \(N(\mu,\sigma^2)\) con \(\sigma^2\) desconocida, la función de log-verosimilitud es:
\[\begin{equation*} \ell(\mu,\sigma^2\mid X) = \ln f_n(X\mid \mu,\sigma^2) = -\frac{n}{2}\ln(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^n(X_i-\mu)^2. \end{equation*}\]
Si fijamos \(\mu=\bar{X}_n\) y derivamos con respecto a \(\sigma^2\), obtenemos:
\[\begin{align*} \frac{\partial}{\partial\sigma^2} \ell(\mu,\sigma^2\mid X) &= \frac{\partial}{\partial\sigma^2} \left[ -\frac{n}{2}\ln(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^n(X_i-\bar{X})^2 \right] \\ &= -\frac{n}{2\sigma^2} + \frac{1}{2(\sigma^2)^2} \sum_{i=1}^n(X_i-\bar{X}_n)^2 = 0 \\ \end{align*}\]
De la última igualdad, obtenemos que:
\[\begin{align*} \frac{n}{2\sigma^2} &= \frac{1}{2(\sigma^2)^2} \sum_{i=1}^n(X_i-\bar{X}_n)^2 \\ \hat\sigma^2 &= \frac{1}{n}\sum_{i=1}^n(X_i-\bar{X}_n)^2 \end{align*}\]
Esta es la fórmula para la varianza muestral.
Las condiciones de segundo orden para verificar que es un máximo se dejan como ejercicio para el lector.
Ejemplo 5.5 (Visualización de la función de verosimilitud) Ahora observe como quedaría la verosimilitud si variamos al mismo tiempo \(\mu\) y \(\sigma\).
Primero, generemos datos aleatorios de una distribución normal para simular una muestra:
Código
set.seed(123)
n <- 100
data <- rnorm(n, mean = 5, sd = 2)Luego, definimos la función de log-verosimilitud:
Código
log_likelihood <- function(mu, sigma_sq, data) {
n <- length(data)
-n / 2 * log(2 * pi * sigma_sq) - (1 / (2 * sigma_sq)) * sum((data - mu)^2)
}Ahora, generamos una grilla de valores para mu y sigma^2 y calculamos la log-verosimilitud para cada combinación:
Código
mu_vals <- seq(4, 6, length.out = 100)
sigma_sq_vals <- seq(2, 5, length.out = 100)
ll_vals <- matrix(0, nrow = length(mu_vals), ncol = length(sigma_sq_vals))
for (i in seq_along(mu_vals)) {
for (j in seq_along(sigma_sq_vals)) {
ll_vals[i, j] <- log_likelihood(mu_vals[i], sigma_sq_vals[j], data)
}
}Y finalmente gráficamos la función de verosimilitud:
Código
df <- expand.grid(mu = mu_vals, sigma_sq = sigma_sq_vals)
df$ll <- as.vector(ll_vals)
ggplot(df, aes(x = mu, y = sigma_sq, z = ll)) +
geom_raster(aes(fill = ll)) +
geom_contour(aes(z = ll), color = "white") +
geom_point(aes(x = mean(data), y = var(data)), color = "red", size = 4) +
scale_fill_viridis_c() +
labs(
title = "Log-verosimilitud en función de mu y sigma^2",
x = expression(mu),
y = expression(sigma^2),
fill = "Log-verosimilitud"
) +
cowplot::theme_cowplot()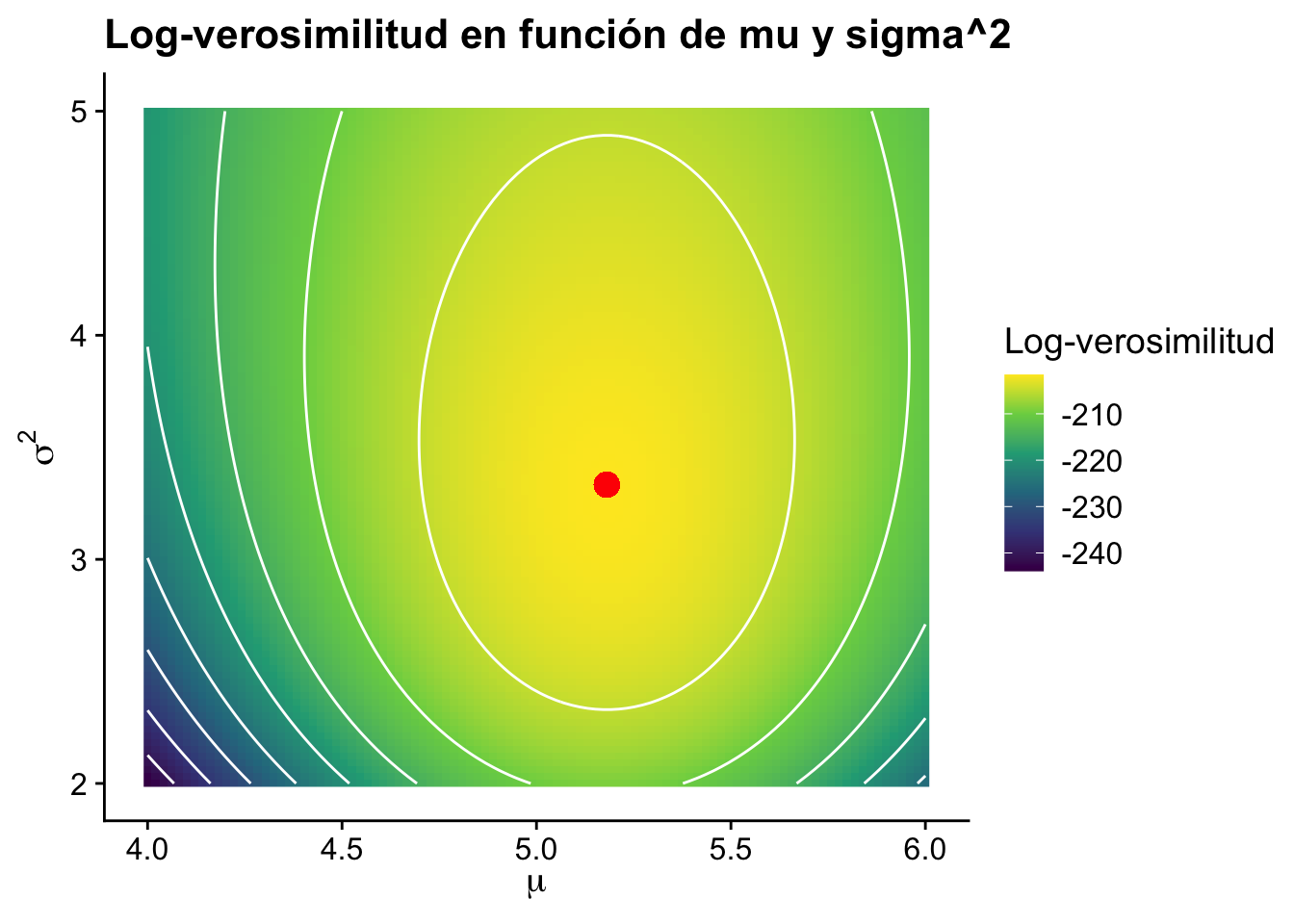
Ejemplo 5.6 Consideremos una muestra \(X_1,\dots, X_n\) que son variables aleatorias independientes e idénticamente distribuidas (i.i.d.) con distribución uniforme en el intervalo \([0,\theta]\), donde \(\theta>0\). Asumimos que cada observación \(X_i>0\).
La función de densidad para esta distribución es:
\[\begin{equation*} f(X\mid\theta)=\frac{1}{\theta}\cdot 1_{[0,\theta]}(x) \end{equation*}\]
Donde \(1_{[0,\theta]}(x)\) es una función indicadora que toma el valor de 1 si \(x\) está en el intervalo \([0,\theta]\) y 0 en caso contrario.
La función de verosimilitud para la muestra es:
\[\begin{equation*} f_n(\theta\mid\theta)=\prod_{i=1}^n f(X_i\mid\theta)=\frac{1}{\theta^n}\prod_{i=1}^n 1_{[0,\theta]}(X_i)=\frac{1}{\theta^n} \prod_{i=1}^n 1_{\{0\leq X_i\leq \theta\}} \quad 0\leq X_i \leq \theta \;\forall i. \end{equation*}\]
Note que \(f_n(\theta\mid\theta)\) es positivo si y solo si \(0\leq X_{(n)}\leq \theta\). donde \(X_{(n)}=\max\{X_1,\dots,X_n\}\) es el estadístico de orden máximo.
El valor de la muestra en la \(i\)-ésima posición, cuando los datos se ordenan de menor a mayor, se denota \(X_{(i)}\) (estadístico de orden). En este caso, \(X_{(n)} = \max\{X_1,\dots, X_n\}\). Entonces \(\hat\theta_{MLE} = X_{(n)}\).
Por ejemplo, si definimos que \(\theta=2\) entonces en ese punto existe una singularidad de la verosimilitud. En términos prácticos, esto significa que la función de verosimilitud no está definida o no es finita en ese punto. Es esencial ser consciente de estas singularidades al trabajar con estimaciones de máxima verosimilitud, ya que pueden afectar los resultados y la interpretación.
Código
x <- runif(100, 0, 2)
n <- length(x)
theta <- seq(1.5, 2.5, length.out = 1000)
L <- numeric(1000)
for (k in 1:1000) {
L[k] <- 1 / theta[k]^n * prod(x < theta[k])
}
ggplot(data.frame(theta, L), aes(x = theta, y = L)) +
geom_line(linewidth = 2) +
geom_vline(
aes(xintercept = max(x)),
color = "red",
linetype = "dashed",
linewidth = 2
) +
labs(
title = "Función de verosimilitud para diferentes valores de theta",
x = expression(theta),
y = "Verosimilitud"
) +
theme_minimal()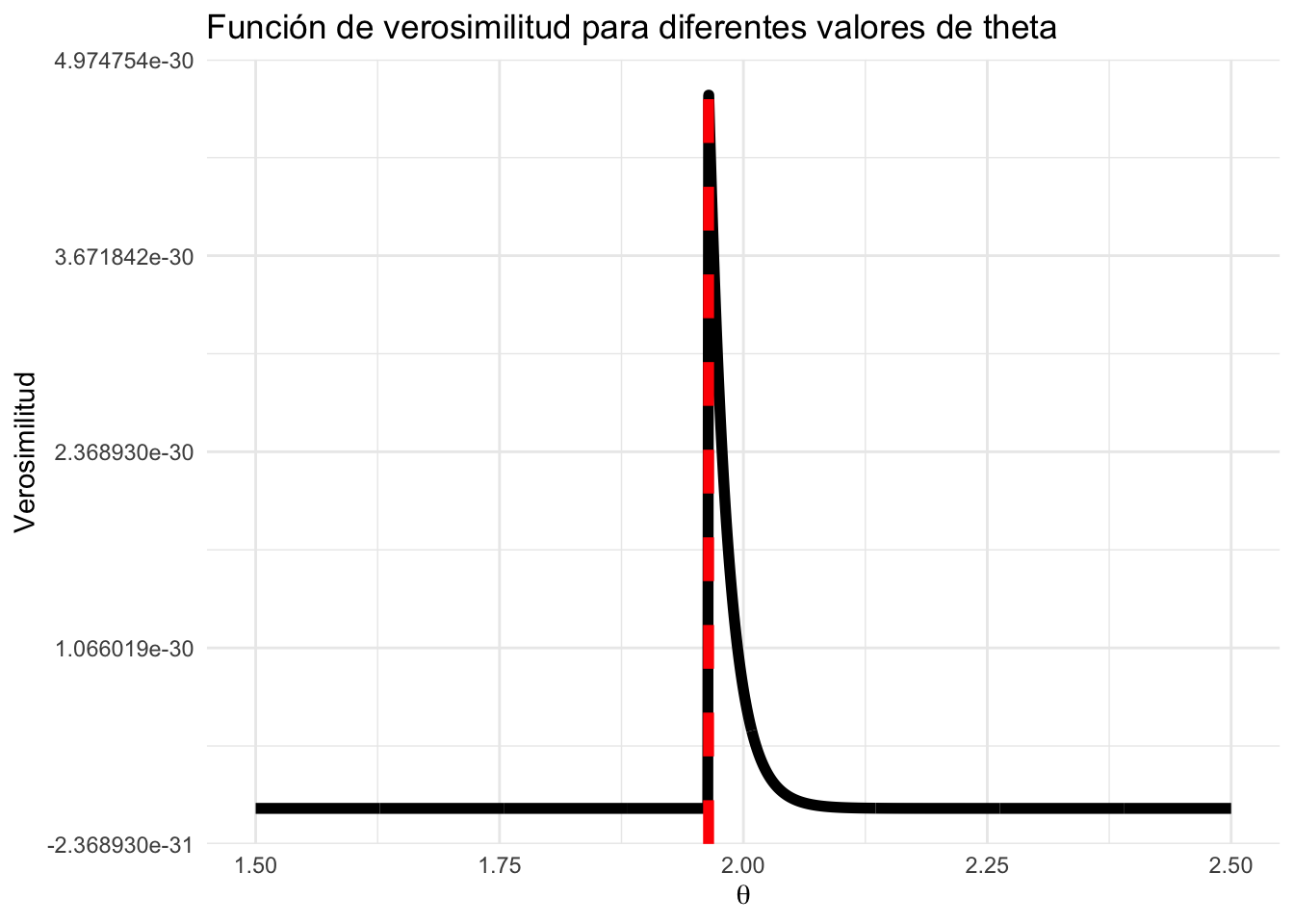
5.1 Propiedades de los estimadores de máxima verosimilitud
5.1.1 Propiedad de invarianza
Teorema 5.1 Si \(\hat\theta\) es el MLE de \(\hat\theta\) y si \(g\) es biyectiva, entonces \(g(\theta)\) es el MLE de \(g(\theta)\).
Prueba. Sea \(\Omega\) el espacio paramétrico \(g(\Omega)\). Dado que \(g\) es biyectiva entonces defina la inversa de \(g\) como \(\theta = g^{-1}(\psi), \psi \in \Omega\). Al reparametrizar la función de verosimilitud, tenemos:
\[\begin{equation*} f_n(x\mid\theta)=f_n(x\mid g^{-1}(\psi)) \end{equation*}\]
El MLE de \(\psi\) es \(\hat\psi\) y satisface que \(f_n(x\mid g^{-1}(\hat\psi))\) es máximo. Dado que \(f_n(x\mid\theta)\) se maximiza cuando \(\theta = \hat \theta\), entonces \(f_n(x\mid g^{-1}(\psi))\) se maximiza cuando \(\hat \theta = g^{-1}(\psi)\) para algún \(\psi\). Por lo tanto, si \(\hat\theta = g^{-1}(\hat\psi)\) entonces \(\hat\psi = g(\hat \theta)\).
Ejemplo 5.7 Suponga que para el caso exponencial se tiene que el MLE de \(\theta\) es \(\hat{\theta}= \bar{X}_n\). Si se quiesiera el MLE de \(\dfrac{1}{\theta}\) entonces se tiene que \(g(\theta) = \dfrac{1}{\theta}\) y \(g^{-1}(\psi) = \dfrac{1}{\psi}\). Por lo tanto, el MLE de \(\dfrac{1}{\theta}\) es \(\dfrac{1}{\bar{X}_n}\).
¿Qué pasa si \(h\) no es biyectiva?
Definición 5.3 (Generalización del MLE) Si \(g\) es una función de \(\theta\) y \(G\) la imagen de \(\Omega\) bajo \(g\). Para cada \(t\in G\) defina \[ G_t = \{\theta: g(\theta) = t\}\] Defina \(L^*(t) = \displaystyle\max_{\theta\in G_t} \ln f_n(x|\theta)\). El MLE de \(g(\theta)\) es igual a un valor \(\hat t\) y satisface \(L^*(\hat t) = \displaystyle\max_{t \in G} L^*(t)\).
Teorema 5.2 Si \(\hat{\theta}\) es el MLE de \(\theta\) entonces \(g(\hat\theta)\) es el MLE de \(g(\theta)\) (\(g\) es arbitraria).
Prueba. Basta probar que \(L^*(\hat t) = \ln f_n(x|\hat \theta)\). Se cumple que \(\hat\theta\in G_{\hat t}\). Como \(\hat \theta\) maximiza \(f_n(x|\theta)\) \(\forall \theta\), también lo hace si \(\theta \in G_{\hat t}\). Entonces \(\hat t = g(\hat \theta)\) (no pueden existir 2 máximos en un conjunto con la misma imagen).
Ejemplo 5.8 Considere una muestra \(X_1,\dots, X_n\sim N(\mu,\sigma^2)\).
- El MLE de \(\mu\) es \(\bar{X}_n\).
- El MLE de \(\sigma^2\) es \(\hat\sigma^2 = \dfrac{1}{n}\sum_{i=1}^n (X_i-\bar{X}_n)^2\).
- Si \(g(\mu,\sigma^2) = \sqrt{\sigma^2}\) entonces el MLE de \(\sqrt{\sigma^2}\) es \(\sqrt{\hat\sigma^2} = \sqrt{\dfrac{1}{n}\sum_{i=1}^n (X_i-\bar{X}_n)^2}\).
- Si \(g(\mu,\sigma^2) = \dfrac{\sigma}{\mu}\) entonces el MLE de \(\dfrac{\sigma}{\mu}\) es \(\dfrac{\hat\sigma}{\bar{X}_n}\).
- Si \(g(\mu,\sigma^2) = \mu^2+\sigma^2\) entonces el MLE de \(\mu^2+\sigma^2\) es \(\bar{X}_n^2 + \hat\sigma^2\).
Observación. Si \(\theta_{MLE}\) de \(\theta\), entonces \(h(\theta_{MLE})\) es el MLE de \(h(\theta)\).
5.1.2 Consistencia
Definición 5.4 Un estimador \(\hat{\theta}_n\) proveniente de la muestra \(X_1, \dots, X_n\) se dice consistente si para cada \(\epsilon>0\) y \(\theta \in \Omega\) \[\begin{equation*} \lim_{n\to\infty} \mathbb{P}(\vert \hat{\theta}_n-\theta\vert<\epsilon) = 1. \end{equation*}\]
Denotamos esta convergencia como
\[\hat{\theta}_{n} \xrightarrow[n\to \infty]{\mathbb P}\theta.\]
Informalmente, la definición anterior dice que a medida que el tamaño de la muestra se vuelve infinito (y la información de la muestra se vuelve cada vez mejor), el estimador estará arbitrariamente cerca del parámetro con alta probabilidad, una propiedad eminentemente deseable. O, cambiando las cosas, podemos decir que la probabilidad de que una secuencia consistente de estimadores no alcance el parámetro verdadero es pequeña.
Recordemos que los estimadores bayesianos son de la forma \[\begin{equation*} W_{1}\mathbb{E}[\text{Previa}] + W_2 \hat\theta_{MLE}. \end{equation*}\] El estimador bayesiano “combina” la esperanza de la previa y el \(\hat\theta_{MLE}\). El \(\hat\theta_{MLE}\) hereda la consistencia del estimador bayesiano si \(n\) tiende a infinito. Eso si, se debe garantizar que \(\lim_{n\to\infty} \mathrm{Var}(\hat{\theta}*{n}) = 0\) y \(\lim_{n\to\infty} \mathrm{Bias}(\hat{\theta}_{n}) = 0\). Bajo estas condiciones entonces
\[\hat\theta_{MLE} \xrightarrow[n\to \infty]{\mathbb P}\theta.\]
5.2 Cálculo numérico
5.2.1 Método de los momentos
El método de los momentos es una técnica de estimación que utiliza los momentos muestrales para estimar los parámetros de una distribución. A continuación, se presentan algunas propiedades y ejemplos de esta técnica.
Ejemplo 5.9 Consideremos una muestra \(X_1,\dots, X_n\) que sigue una distribución Gamma \(\Gamma(\alpha,1)\). Estamos interesados en estimar el parámetro \(\alpha\). La función de densidad de la distribución Gamma es dada por:
\[\begin{equation*} f(x\mid\alpha)=\frac{1}{\Gamma(\alpha)}x^{\alpha-1}e^{-x} \end{equation*}\]
La función de verosimilitud asociada es:
\[\begin{equation*} f_n(x\mid\alpha)=\frac{1}{\Gamma(\alpha)^n}\prod_{i=1}^n x_i^{\alpha-1}e^{-x_i} \end{equation*}\]
Para encontrar el estimador de máxima verosimilitud (MLE) de \(\alpha\), derivamos la log-verosimilitud con respecto a \(\alpha\) y la igualamos a cero:
\[\begin{align*} \frac{\partial}{\partial\alpha} \ell(\alpha\mid X) &= \frac{\partial}{\partial\alpha} \left[ -n\ln \Gamma(\alpha) + (\alpha-1)\sum_{i=1}^n \ln X_i - \sum_{i=1}^n X_i \right] \\ &= -n\frac{1}{\Gamma(\alpha)}\frac{\partial}{\partial\alpha}\Gamma(\alpha) + \sum_{i=1}^n \ln X_i = 0 \\ \end{align*}\]
El problema con este cálculo es que no existe una expresión cerrada para la derivada de la función Gamma. Usualmente se hacen aproximaciones numéricas.
Definición 5.5 Supongamos que tenemos una muestra \(X_1,\dots, X_n\) que sigue una distribución \(F\), indexada por un parámetro \(\theta\) que reside en \(\mathbb{R}^k\), y que tiene al menos \(k\) momentos finitos. Para \(j=1,\dots,k\), definimos \(\mu_j(\theta)=\mathbb{E}[X_1^j\mid\theta]\). Asumimos que la función \(\mu(\theta)=(\mu_1(\theta),\dots,\mu_2(\theta))\) es biyectiva. Definimos \(M\) como la inversa de \(\mu\), es decir,
\[\begin{equation*} M(\mu(\theta))=\theta=M(\mu_1(\theta),\dots,\mu_2(\theta)) \end{equation*}\]
y definimos los momentos empíricos como:
\[\begin{equation*} m_j=\frac{1}{n}\sum_{i=1}^n X_i^j, \quad j=1,\dots, k. \end{equation*}\]
El estimador de máxima verosimilitud (MLE) según el método de los momentos es:
\[\begin{equation*} \hat\theta = M(m_1,\dots,m_k). \end{equation*}\]
Ejemplo 5.10 Del ejemplo anterior, \(\mu_1(\alpha) = \mathbb{E}[x_1|\alpha] = \alpha\).Dado que \(m_1 = \hat x_n\), el sistema por resolver es \[ \mu_1(\alpha) = m_1 \Longleftrightarrow \alpha = \bar x_n\] El estimador por método de momentos es \(\hat \alpha = \bar{X}_n\).
Ejemplo 5.11 Consideremos una muestra \(X_1,\dots, X_n\) que sigue una distribución \(\mathrm{Gamma}(\alpha,\beta)\). Sabemos que la media es \(\mu=\alpha/\beta\) y la varianza es \(\sigma^2=\alpha/\beta^2\). Por lo tanto el segundo momento es
\[\begin{equation*} \mathbb{E}[X^2] = \mathrm{Var}(X) + \mathbb{E}[X]^2 = \frac{\alpha}{\beta^2} + \left(\frac{\alpha}{\beta}\right)^2 = \frac{\alpha(\alpha+1)}{\beta^2} \end{equation*}\]
Para encontrar los estimadores de \(\alpha\) y \(\beta\), necesitamos resolver el siguiente sistema de ecuaciones:
\[\begin{equation*} \begin{cases} \mu_1(\theta) = \dfrac{\alpha}\beta = \bar{X}_n = m_1& (1)\\ \mu_2(\theta) = \dfrac{\alpha(\alpha+1)}{\beta^2}=m_2 & (2) \end{cases} \end{equation*}\]
De \((1)\), \(\alpha = m_1\beta\). Sustituyendo en \((2)\),
\[m_2 = \dfrac{m_1\beta(m_1\beta+1)}{\beta^2} = m_1^2+\dfrac{m_1}\beta = m_2\implies m_2-m_1^2 = \dfrac{m_1}{\beta}.\] De esta manera, \[ \hat\beta = \dfrac{m_1}{m_2-m_1^2},\quad \hat\alpha = \dfrac{m_1^2}{m_2-m_1^2}\]
Teorema 5.3 Supongamos que \(X_1,\dots, X_n\) son variables aleatorias independientes e idénticamente distribuidas (i.i.d) con una distribución indexada por \(\theta\in\mathbb{R}^k\). Si los \(k\) momentos teóricos son finitos para todo \(\theta\) y \(M\) es una función continua, entonces el estimador obtenido mediante el método de los momentos es consistente.
5.3 Laboratorio
Suponga que tenemos una tabla con los siguientes datos, los cuales representan la cantidad de giros hacia la derecha en cierta intersección.
Código
(X <- c(
rep(0, 14),
rep(1, 30),
rep(2, 36),
rep(3, 68),
rep(4, 43),
rep(5, 43),
rep(6, 30),
rep(7, 14),
rep(8, 10),
rep(9, 6),
rep(10, 4),
rep(11, 1),
rep(12, 1)
)) [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1
[26] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2
[51] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[76] 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
[101] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
[126] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4
[151] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
[176] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5
[201] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
[226] 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6
[251] 6 6 6 6 6 6 6 6 6 6 6 6 6 6 7 7 7 7 7 7 7 7 7 7 7
[276] 7 7 7 8 8 8 8 8 8 8 8 8 8 9 9 9 9 9 9 10 10 10 10 11 12Queremos ajustar esta tabla a una distribución Poisson con función de densidad
\[ \mathbb{P}(X=x) = \frac{\lambda^x e^{-\lambda}}{x!} \]
Se puede probar que teórico de máxima verosimilitud para \(\lambda\) es \(\overline{X}\) (Tarea). Queremos estimar este parámetro alternativamente maximizando la función de verosimilitud.
Primero veamos la forma de los datos,
Código
hist(X, main = "Número de giros a la derecha", right = FALSE, prob = TRUE)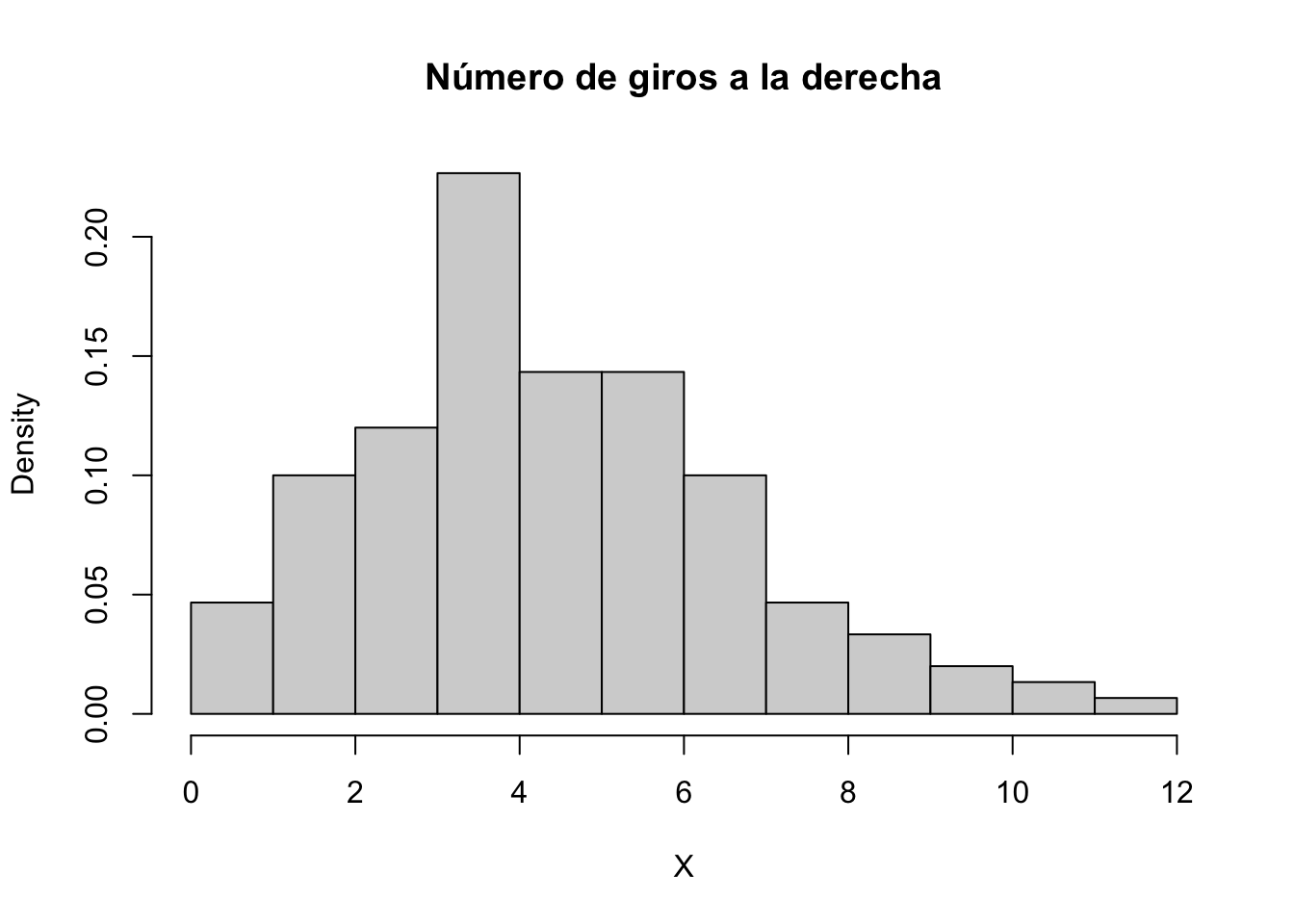
Definamos la función correspondiente como \(-\log(\mathbb{P}(X=x))\)
Código
n <- length(X)
negloglike <- function(lambda) {
n * lambda - sum(X) * log(lambda) + sum(log(factorial(X)))
}Para encontrar el parámetro deseado, basta minimizar la función negloglike usando el la instrucción de optimización no lineal optim.
Código
lambda_hat <- optim(par = 0.5, fn = negloglike, hessian = TRUE)Aquí el valor par = c(0.5) representa un valor inicial de búsqueda y hessian = TRUE determina el cálculo explícito de la segunda derivada.
Compare el resultado de lambda.hat$estimate con mean(X) el cual sería el estimador por el método de los momentos.
Código
lambda_hat$par[1] 3.892969Código
mean(X)[1] 3.893333