12  Pruebas parámetricas clásicas

12.1 Prueba \(t\) de Student

La prueba \(t\) de Student se usa cuando no conocemos ni la media (\(\mu\)) ni la desviación estándar (\(\sigma\)) de nuestra población.

Supongamos que tenemos una muestra \(X_1,\dots, X_n\) de una distribución normal con media \(\mu\) y varianza \(\sigma^2\), ambas desconocidas. Queremos probar las siguientes hipótesis:

• Hipótesis nula (\(H_0\)): \(\mu\leq\mu_0\)
• Hipótesis alternativa (\(H_1\)): \(\mu>\mu_0\)

Definimos el estadístico de prueba \(U\) como la diferencia entre la media muestral y la media de la hipótesis nula, normalizada por la desviación estándar muestral y ajustada por el tamaño de la muestra, es decir,

\(U = \dfrac{\bar X_n -\mu_0}{s /\sqrt n}\).

Si \(\mu=\mu_0\), entonces \(U\) sigue una distribución t de Student con \(n-1\) grados de libertad, es decir, \(U \sim t_{n-1}\). La decisión de rechazar la hipótesis nula se basa en el valor observado de \(U\).

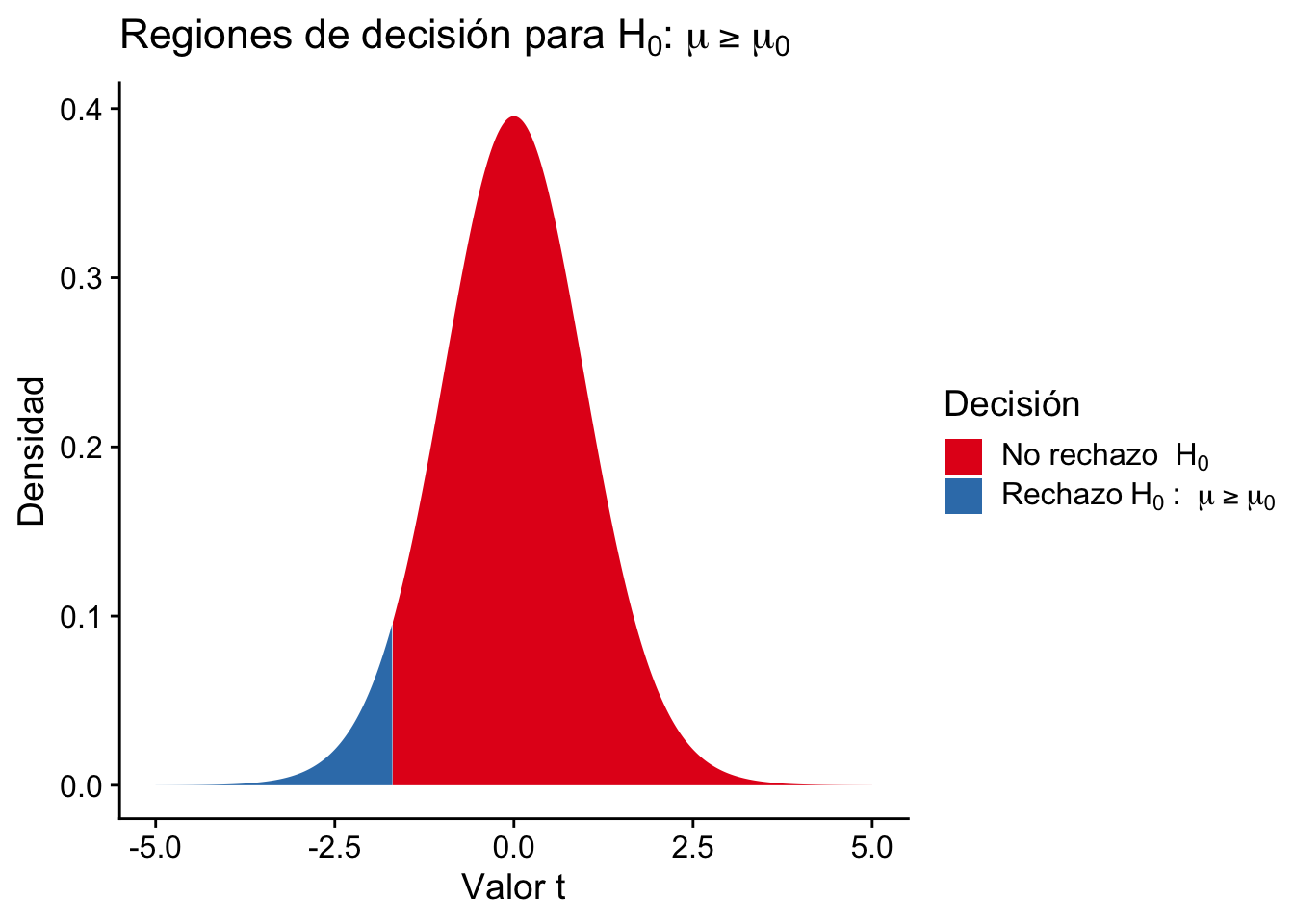
Si estamos probando la hipótesis nula \(H_0: \mu\leq\mu_0\) vs la hipótesis alternativa \(H_1: \mu>\mu_0\), rechazamos \(H_0\) si \(U\geq c\), donde \(c\) es el valor crítico de la distribución t correspondiente al nivel de significancia elegido.

Por otro lado, si estamos probando la hipótesis nula \(H_0: \mu\geq\mu_0\) vs la hipótesis alternativa \(H_1: \mu<\mu_0\), rechazamos \(H_0\) si \(U\leq c\).

Ejemplo 12.1 En el trabajo de (Smith, Piland, y Fisher 1992) usó un recopilación de datos del departamento de salud Nuevo México en 1988 en casas de cuido oficiales. En esta base se tiene los días de hospitalización de cada paciente.

Cargamos los datos y vemos cómo está la estructura de la base:

load("./data/Nursing.rda")
knitr::kable(summary(Nursing))

	Beds	InPatientDays	AllPatientDays	PatientRevenue	NurseSalaries	FacilitiesExpend	Rural
	Min. : 25.00	Min. : 48.0	Min. : 83.0	Min. : 2853	Min. :1288	Min. : 137	Min. :0.0000
	1st Qu.: 62.00	1st Qu.:125.2	1st Qu.:198.0	1st Qu.: 8857	1st Qu.:2336	1st Qu.:1229	1st Qu.:0.0000
	Median : 88.00	Median :164.5	Median :279.0	Median :12384	Median :3696	Median :2378	Median :1.0000
	Mean : 93.27	Mean :183.9	Mean :280.2	Mean :14210	Mean :3813	Mean :2848	Mean :0.6538
	3rd Qu.:120.00	3rd Qu.:229.0	3rd Qu.:363.8	3rd Qu.:18777	3rd Qu.:4840	3rd Qu.:4444	3rd Qu.:1.0000
	Max. :244.00	Max. :514.0	Max. :776.0	Max. :36029	Max. :7489	Max. :6442	Max. :1.0000

Ahora, hacemos un histograma para visualizar la distribución de los días de hospitalización:

hist(Nursing$InPatientDays)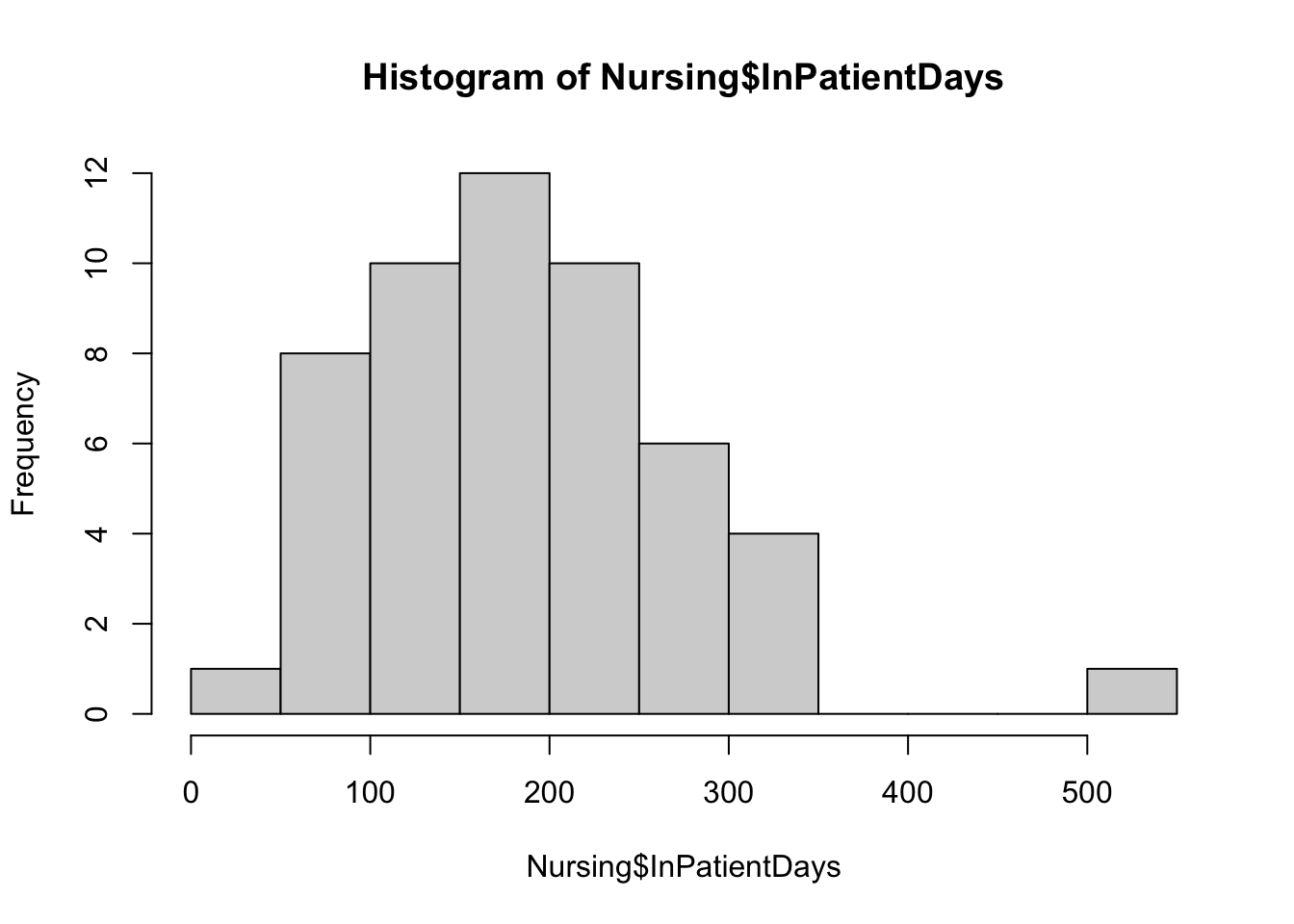

Observamos que la media es alrededor de 183 días. Ahora, supongamos que los responsables del hogar de cuidado quieren saber si los pacientes tienen estancias más cortas que 200 días.

Por lo tanto, queremos probar la hipótesis de \(H_{0}: \mu \leq 200\) versus \(H_{1}: \mu > 200\). Si rechazamos \(H_{0}\), entonces los pacientes se quedan en el hogar de cuidados por más de 200 días en promedio.

El estadístico de prueba está dado por \[\begin{equation*} U = \sqrt{n} \frac{(\overline{X} - \mu)}{s} \end{equation*}\]

y rechazaremos \(H_{0}\) si \(U>t_{n-1, 1-\alpha}\).

Calculamos los valores necesarios para llevar a cabo la prueba:

x <- Nursing$InPatientDays
n <- length(x)
xbar <- mean(x)
s <- sd(x)
alpha <- 0.1
mu0 <- 200

(quantil_t <- qt(p = 1 - alpha, df = n - 1))

[1] 1.298373

(U <- sqrt(n) * (xbar - 200) / s)

[1] -1.336882

Finalmente, comprobamos si el estadístico de prueba es mayor que el valor crítico para decidir si rechazamos \(H_0\):

U > quantil_t

[1] FALSE

Recordemos que el valor \(p\) de los datos observados y una prueba específica es el \(\alpha\) más pequeño, de modo que rechazaríamos la hipótesis nula en el nivel de significancia \(\alpha\).

Para la prueba \(t\) que acabamos de realizar, el valor \(p\) es \(P(T_{52-1}>-1.3369)\), donde \(T_{52-1}\) es una variable aleatoria con distribución \(t\) de Student con 51 grados de libertad. Es decir:

pt(U, df = n - 1, lower.tail = FALSE)

[1] 0.9064029

El lenguaje R tiene una función para realizar la prueba de hipótesis de una media poblacional. La función t.test tiene la siguiente sintaxis:

t.test(x, mu = mu0, alternative = "greater", conf.level = 0.90)

    One Sample t-test

data:  x
t = -1.3369, df = 51, p-value = 0.9064
alternative hypothesis: true mean is greater than 200
90 percent confidence interval:
 168.1955      Inf
sample estimates:
mean of x 
 183.8654 

12.1.1 Prueba \(t\) pareada

La idea principal del test \(t\) de pares es simplificar una situación de dos muestras, donde comparamos dos medias, a una situación de una única muestra donde hacemos inferencia sobre una sola media y luego usamos un test \(t\) simple. En este escenario, podemos reducir fácilmente los datos brutos a un conjunto de diferencias y realizar una prueba \(t\) de una sola muestra. De esta manera, simplificamos nuestro procedimiento de inferencia a un problema donde estamos haciendo una inferencia sobre una sola media: la media de las diferencias. En otras palabras, al reducir las dos muestras a una muestra de diferencias, estamos esencialmente reduciendo el problema de un caso en el que estamos comparando dos medias a un problema en el que estamos estudiando una media.

En otras palabras, esta prueba está diseñada para muestras dos muestras que están organizadas en \(n\) pares. Acá, tenemos una misma variable pero medida bajo dos condiciones distintas. Lo que se quiere determinar es si la primera condición aumenta, disminuye o es igual con respecto a la segunda.

Ejemplo 12.2 La conducción bajo los efectos del alcohol es una de las principales causas de accidentes de tráfico. Se seleccionó una muestra de 20 conductores y se midió su tiempo de reacción en un circuito de obstáculos antes y después de beber dos cervezas. El objetivo de este estudio era verificar si los conductores se ven afectados después de beber dos cervezas. Para cada población tenemos el tiempo medio de reacción, \(μ_1\) para la población 1 (sin alcohol) y \(μ_2\) para la población 2 (dos cervezas). Se usaron los mismo mismos conductores para generar las muestras para ambas poblaciones. Definimos \(\mu_d = \mu_1 - \mu_2\).

cerveza <- read.csv("./data/beers.csv")
head(cerveza)

  Before After
1   6.25  6.85
2   2.96  4.78
3   4.95  5.57
4   3.94  4.01
5   4.85  5.91
6   4.81  5.34

ggplot(cerveza, aes(x = Before, y = After)) +
  geom_point() +
  geom_abline(intercept = 0, slope = 1, color = "red") +
  labs(
    x = "Tiempo de reacción antes de beber",
    y = "Tiempo de reacción después de beber"
  ) +
  cowplot::theme_cowplot()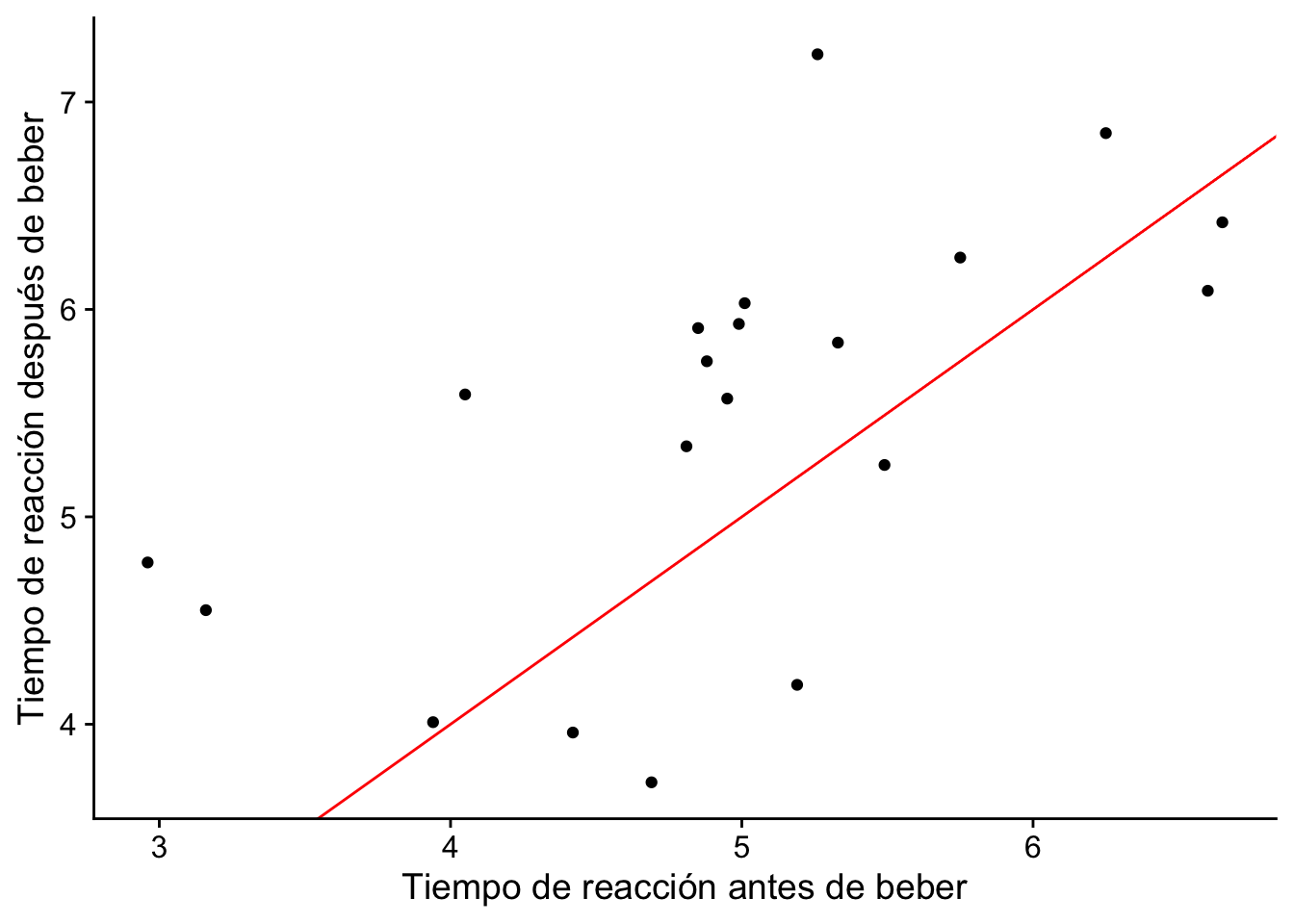

Debemos primero establecer la diferencia de cada variable:

cerveza <- cerveza %>%
  mutate(Diferencia = Before - After)
head(cerveza)

  Before After Diferencia
1   6.25  6.85      -0.60
2   2.96  4.78      -1.82
3   4.95  5.57      -0.62
4   3.94  4.01      -0.07
5   4.85  5.91      -1.06
6   4.81  5.34      -0.53

Nuestro interés es conocer si el tiempo de reacción después de beber es igual que el tiempo de reacción antes de beber. Por lo tanto, nuestra prueba de hipótesis es:

\[\begin{equation*} H_0: \mu_d = 0 \quad vs \quad H_1: \mu_d \neq 0 \end{equation*}\]

En este caso el estadístico de pruebna sería \[\begin{equation*} U = \frac{\bar{X}_n - \mu_0}{s / \sqrt{n}} \end{equation*}\] y la hipótesis \(H_0\) se rechaza si \(|U|>t_{n-1,1-\alpha/2}\).

Para calcular el estadístico de prueba, hacemos los siguientes cálculos:

n <- nrow(cerveza)
media_d <- mean(cerveza$Diferencia)
desv_d <- sd(cerveza$Diferencia)

(U <- (media_d - 0) / (desv_d / sqrt(n)))

[1] 2.582059

(quantil_t <- qt(p = 0.975, df = n - 1))

[1] 2.093024

Rechazamos la hipótesis nula

abs(U) > quantil_t

[1] TRUE

(p_valor <- 2 * pt(q = abs(U), df = n - 1, lower.tail = FALSE))

[1] 0.01827078

O usando la función t.test:

t.test(cerveza$Before, cerveza$After, paired = TRUE, alternative = "two.sided")

    Paired t-test

data:  cerveza$Before and cerveza$After
t = -2.5821, df = 19, p-value = 0.01827
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -0.90801734 -0.09498266
sample estimates:
mean difference 
        -0.5015 

Importante

En el ejemplo anterior, note que en el intervalo de confianza, el cero no está incluido. Esto es equivalente a rechazar la hipótesis nula ya que significa que \(\mu_d=0\) no es una opción viable dentro de las posibilidades del intervalo.

12.1.2 Prueba de comparación de medias en 2 poblaciones

Hemos hablado sobre el caso de la muestra dependiente, donde las observaciones están emparejadas o vinculadas entre las dos muestras. Ahora discutiremos el caso de la muestra independiente. En este caso, todos los individuos son independientes de todos los demás individuos en su muestra, así como de todos los individuos en la otra muestra. Esto se logra, en la mayoría de los casos, tomando una muestra aleatoria de cada uno de los dos grupos en estudio o dividiendo una muestra aleatoria de toda la población en dos submuestras basadas en la variable de agrupación de interés.

Tomamos una muestra \(X_1, \dots, X_{m} \sim N(\mu_1, \sigma^2)\) y una muestra \(Y_1, \dots, Y_{n} \sim N(\mu_2, \sigma^2)\) de dos poblaciones independientes. Los parámetros desconocidos son \(\mu_1, \mu_2, \sigma^2\). Asumimos que \((X_i, Y_i)\) son independientes y que la varianza es la misma (homocedasticidad).

Lo primero que debemos es establecer un estadístico apropriado para probar la hipótesis del problema. Defina

\[\begin{align*} \overline{X}_{m} &= \frac{1}{m} \sum_{i=1}^{m} X_i, \\ \overline{Y}_{n} &= \frac{1}{n} \sum_{i=1}^{n} Y_i, \\ s_{X}^2 &= \frac{1}{m - 1} \sum_{i=1}^{m} (X_i - \overline{X}_{m})^2, \\ s_{Y}^2 &= \frac{1}{n - 1} \sum_{i=1}^{n} (Y_i - \overline{Y}_{n})^2. \end{align*}\]

Entonces considere el estadístico

\[\begin{equation*} U = \frac{\overline{X}_m - \overline{Y}_n}{\sqrt{\frac{1}{m} + \frac{1}{n}} \sqrt{\frac{(m - 1) s_{X}^2 + (n - 1) s_{Y}^2}{m + n - 2}}}. \end{equation*}\]

Importante

Bajo la hipotesis nula \(\mu_1=\mu_2\), se puede demostrar que \(U\sim t_{m+n-2}.\)

Una vez con el estadístico de prueba y su distribución, se aplican los mismo principios que hemos visto anteriormente.

Ejemplo 12.3 Recordemos el caso de las nubes tratadas con sulfato de plata. Queremos probar si el tratamiento aumenta la lluvia. Para esto consideramos las siguientes hipótesis:

\[ H_0: \mu_{\text{con trat.}} \leq \mu_{\text{sin trat.}} \quad vs \quad H_1: \mu_{\text{con trat.}} > \mu_{\text{sin trat.}} \]

nubes <- read.table(
  file = "./data/clouds.txt",
  sep = "\t", header = TRUE
)
log_lluvia <- log(nubes)

n <- nrow(nubes)

con_tratamiento <- log_lluvia$Seeded.Clouds
sin_tratamiento <- log_lluvia$Unseeded.Clouds

(xbar <- mean(con_tratamiento))

[1] 5.134187

(ybar <- mean(sin_tratamiento))

[1] 3.990406

(s2_x <- var(con_tratamiento))

[1] 2.558444

(s2_y <- var(sin_tratamiento))

[1] 2.695663

 nubes %>%
   rename(
   "Con tratamiento"  = "Seeded.Clouds",
   "Sin tratamiento" = "Unseeded.Clouds"
   ) %>%
   pivot_longer(
     cols = everything(),
     names_to = "Tratamiento", values_to = "valor"
   ) %>%
   ggplot(aes(x = log(valor), fill = Tratamiento
             )) +
   geom_histogram(bins = 10, alpha = 0.5, color="black") +
   geom_vline(
     xintercept = mean(con_tratamiento),
     color = "blue", linetype = "dashed", linewidth = 2
   ) +
   geom_vline(
     xintercept = mean(sin_tratamiento),
     color = "red", linetype = "dashed", linewidth = 2
   ) +
   scale_fill_manual(values = c(
      "Con tratamiento" = "blue",
      "Sin tratamiento" = "red"
   )) +
   labs(x = "log-precipitación", y = "Frecuencia") +
   cowplot::theme_cowplot()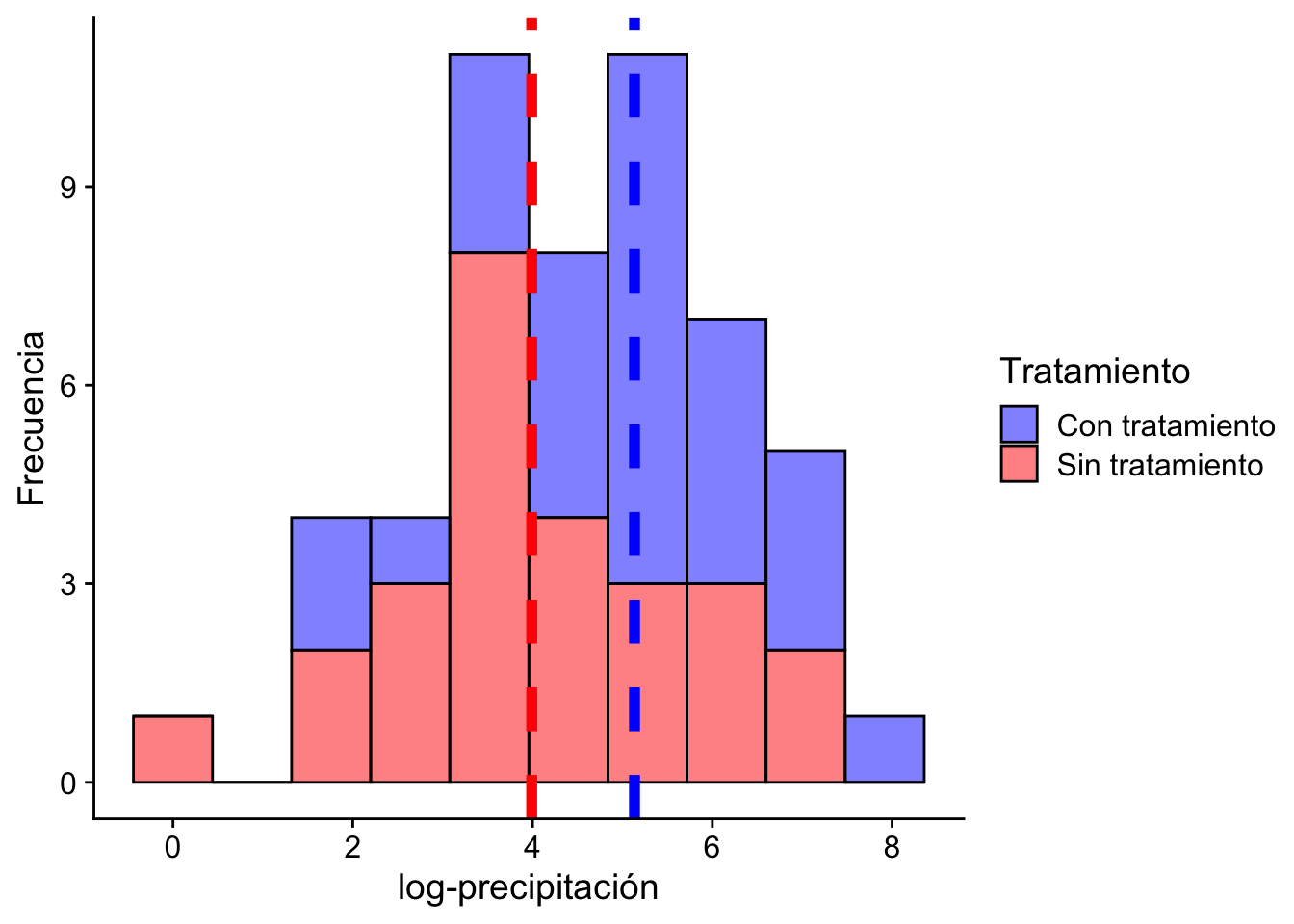

Entonces el estadístico que queremos construir para comparar la medias es (OJO en este caso \(m=n\) porque tienen la misma cantidad de datos):

(U <- sqrt(n + n - 2) * (xbar - ybar) /
  (sqrt(1 / n + 1 / n) * sqrt((n - 1) * s2_x + (n - 1) * s2_y)))

[1] 2.544369

Por tanto se debe comparar con una \(t\)-student con \(26+26 - 2 = 50\) grados de libertad. Asuma un \(\alpha = 0.01\). Para rechazar la hipótesis nula se debe cumplir que \(U > t_{50, .99}\). Entonces calculamos el valor crítico:

(qnt <- qt(p = 1 - 0.01, df = n + n - 2))

[1] 2.403272

En este punto, ejecutamos nuestra prueba y nos preguntamos si rechazamos o no la hipótesis nula:

U > qnt

[1] TRUE

Para determinar el valor-\(p\) se debe calcular \(1 - T_{50}(U)\), donde \(T_{50}\) es la función de distribución de una \(t\)-student con 50 grados de libertad.

1 - pt(q = U, df = n + n - 2)

[1] 0.007041329

ggplot(data.frame(x = c(-1, 4)), aes(x = x)) +
  stat_function(fun = dt, args = list(df = 50), color = "blue") +
  geom_segment(aes(x = qnt, y = 0, xend = qnt, yend = 0.1),
    color = "blue", linetype = "dashed"
  ) +
  geom_segment(aes(x = U, y = 0, xend = U, yend = 0.15),
    color = "red", linetype = "dashed"
  ) +
  geom_label(aes(
    x = qnt, y = 0.1,
    label = "Valor crítico"
  ), color = "blue", nudgex = -0.5) +
  geom_label(
    aes(
      x = U, y = 0.15,
      label = "Estadístico U"
    ),
    color = "red", nudge_x = 0.5
  ) +
  # label the area of p-value
  geom_label(aes(
    x = (U + 4) / 2, y = 0.01,
    label = "p-value"
  ), color = "black") +
  geom_area(
    stat = "function", fun = dt, args = list(df = 50),
    xlim = c(qnt, U), fill = "blue", alpha = 0.5
  ) +
  geom_area(
    stat = "function", fun = dt, args = list(df = 50),
    xlim = c(U, 4), fill = "red", alpha = 0.5
  ) +
  labs(x = "t", y = "f(t)") +
  cowplot::theme_cowplot()

Warning in geom_label(aes(x = qnt, y = 0.1, label = "Valor crítico"), color =
"blue", : Ignoring unknown parameters: `nudgex`

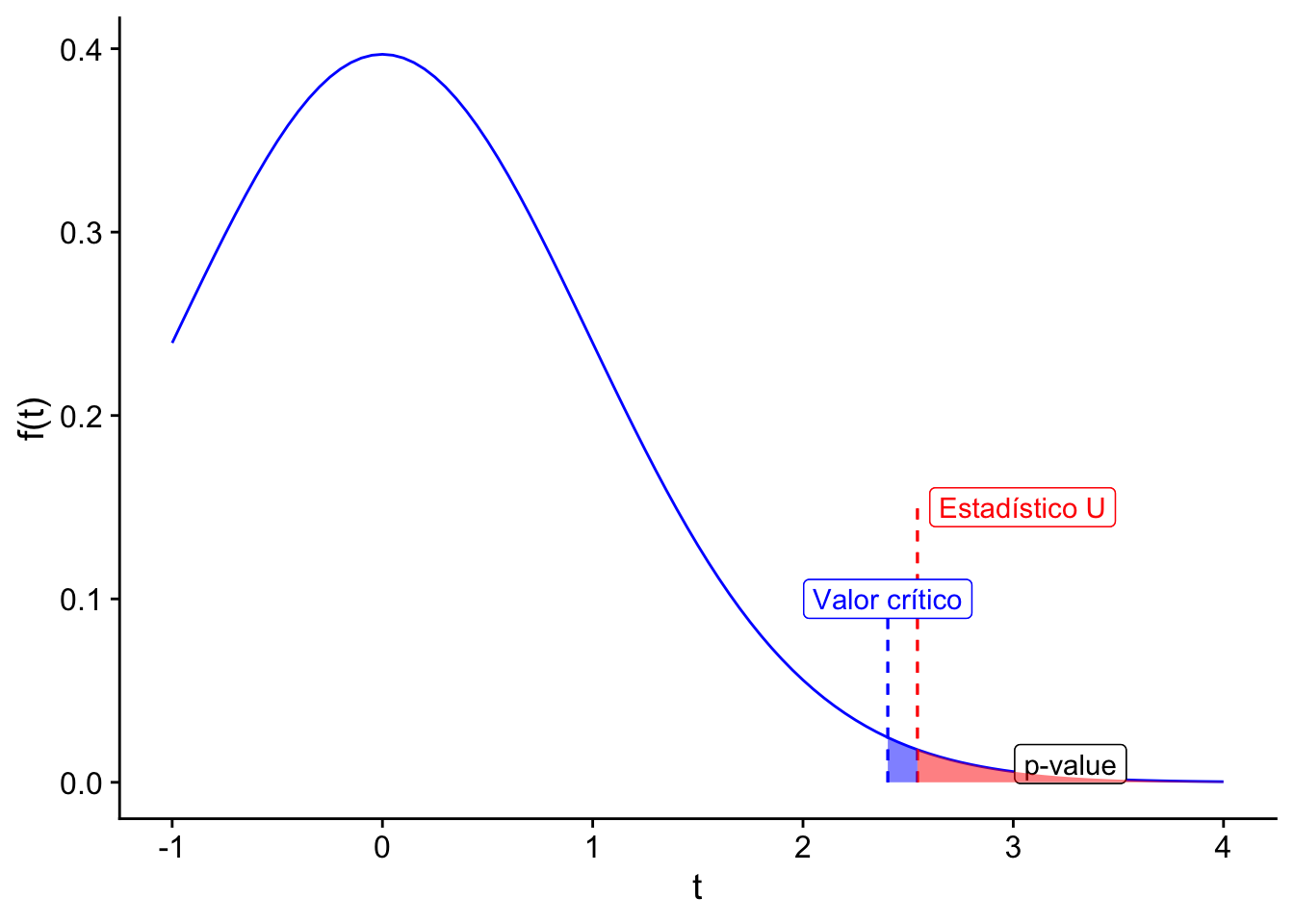
Si usáramos la función t.test de R obtendríamos el mismo resultado:

t.test(
  x = con_tratamiento, y = sin_tratamiento,
  alternative = "greater", mu = 0, var.equal = TRUE,
  conf.level = 0.90
)

    Two Sample t-test

data:  con_tratamiento and sin_tratamiento
t = 2.5444, df = 50, p-value = 0.007041
alternative hypothesis: true difference in means is greater than 0
90 percent confidence interval:
 0.5599649       Inf
sample estimates:
mean of x mean of y 
 5.134187  3.990406 

Interpretación: rechazamos al nivel 1% de significancia la hipótesis de que las nubes irradiadas tienen una log-precipitación media menor a la de las nubes no irradiadas.

Ejemplo 12.4 Suponga que se tienen 8 muestras de una mina de cobre en un lugar 1 y 10 muestras de otra mina en un lugar 2. El ingeniero de la mina se pregunta: ¿Las dos localizaciones generan el mismo nivel de cobre?

Para esto, define \(X_1,\dots,X_8\) la cantidad de cobre (gramos) en el lugar 1, y \(X_1,\dots,X_{10}\) del lugar 2.

En el laboratorio, procesa los datos y obtiene lo siguiente

• \(\bar X_8 = 2.6\)
• \(\bar Y_{10} = 2.3\)
• \(s_X^2 = \frac{0.32}{8-1} = 0.045\)y
• \(s_Y^2=\frac{0.22}{10-1} = 0.025\)

Entonces, para resolver el problema, plantea hacer la prueba de hipótesis

\[ H_0: \mu_1=\mu_2 \quad H_1: \mu_1\neq\mu_2 \]

Con el supuesto que \(X_i\sim N(\mu_1,\sigma^2)\), \(Y_j\sim N(\mu_2,\sigma^2)\).

n <- 8
m <- 10

n + m - 2

[1] 16

xbar <- 2.6
ybar <- 2.3

s2_x <- 0.32/7
s2_y <- 0.22/9
(U <- sqrt(n + m - 2) * (xbar - ybar) /
    (sqrt(1 / n + 1 / m) * sqrt((n - 1) * s2_x + (m - 1) * s2_y)))

[1] 3.442652

El ingeniero decide usar un nivel de significancia de 1%, es decir \(\alpha_0 = 1\%\). Para este caso, el valor crítico es

(qnt <- qt(p = 1 - 0.01 / 2, df = n + m - 2))

[1] 2.920782

Con esta información, el ingeniero se pregunta si rechaza o no la hipótesis nula.

abs(U) > qnt

[1] TRUE

Para cerciorarse, calcula el \(pvalor-\(p\), con la fórmula \(2[1-T_{16}(|3.442|)]\).

2 * (1 - pt(q = U, df = n + m - 2))

[1] 0.003345064

En este caso no podemos usar la función t.test directamente ya que no tenmos los datos reales para corroborar sus resultados. Sin embargo, podemos simular con unos datos ficticios:

x <- rnorm(n = n, mean = xbar, sd = sqrt(s2_x))
y <- rnorm(n = m, mean = ybar, sd = sqrt(s2_y))


t.test(
  x = x, y = y,
  alternative = "two.sided", mu = 0, var.equal = TRUE,
  conf.level = 0.99
)

    Two Sample t-test

data:  x and y
t = 5.8198, df = 16, p-value = 2.61e-05
alternative hypothesis: true difference in means is not equal to 0
99 percent confidence interval:
 0.1817306 0.5479226
sample estimates:
mean of x mean of y 
 2.614007  2.249180 

Interpretación: Rechazamos al 1% de significancia la hipótesis de una diferencia no significativa entre las cantidades medias de cobre en cada localización.

Ejercicio 12.1 Suponga que se quiere hacer una prueba del cociente de verosimilitud para probar la hipótesis nula \(\mu_1\leq \mu_2\) con dos muestras normales, donde las medias son desconocidas y la varianza es igual a ambas muestras pero desconocida.

Escriba el cociente de verosimilitud con estas condiciones y encuentre la regla de decisión correspondiente.

¿Cómo se compara esa regla con la que acabamos de ver en esta sección?

12.2 Prueba \(F\)

Definamos ciertos conceptos. Si tenemos dos variables aleatorias independientes \(Y\) y \(W\), con \(Y\) siguiendo una distribución \(\chi^2_m\) y \(W\) siguiendo una distribución \(\chi^2_n\), podemos definir \(X\) como la proporción \(X = \dfrac{Y/m}{W/n}\)​. En este caso, decimos que \(X\) sigue una distribución \(F\) con \(m\) y \(n\) grados de libertad.

La función de densidad de esta distribución es:

\[\begin{equation*} f(x)= \begin{cases} \displaystyle \frac{\Gamma\left[\frac{1}{2}(m+n)\right] m^{m / 2} n^{n / 2}}{\Gamma\left(\frac{1}{2} m\right) \Gamma\left(\frac{1}{2} n\right)} \cdot \frac{x^{(m / 2)-1}}{(m x+n)^{(m+n) / 2}} & \text{si } x>0 \\ 0 & \text{en otro caso} \end{cases} \end{equation*}\]

Examinemos algunas propiedades de esta distribución.

1. Si \(X\sim F_{m,n}\), entonces \(1/X\sim F_{n,m}\).
2. Si \(Y\) sigue una distribución \(t\) con \(n\) grados de libertad, entonces \(Y^2\) sigue una distribución \(F\) con \(1\) y \(n\) grados de libertad.

Digamos que tenemos dos conjuntos de datos \(X_1,\dots,X_m\) y \(Y_1,\dots,Y_n\), donde \(X_i\sim N(\mu_1,\sigma_{1}^2)\) e \(Y_j\sim N(\mu_2,\sigma_{2}^2)\). Si queremos comparar las varianzas de estos dos conjuntos de datos, podríamos formular la hipótesis nula \(H_0: \sigma_1^2\leq \sigma_2^2\). Con un nivel de significancia \(\alpha\).

Ahora de los capítulos anteriores recuerde que

\[\begin{align*} \frac{(m-1)s_X^2}{\sigma_1^2} & \sim \chi^2_{m-1} \\ \frac{(n-1)s_Y^2}{\sigma_2^2} & \sim \chi^2_{n-1} \end{align*}\]

Bajo el supuesto de homocedasticidad podemos definir el estadístico

\[\begin{align*} V &= \dfrac{\dfrac{(m-1)s_X^2/\sigma_1^2}{m-1}}{\dfrac{(n-1)s_Y^2/\sigma_2^2}{n-1}} \\ &= \frac{s_X^2}{s_Y^2} \sim F_{m-1,n-1} \end{align*}\]

Luego, comparamos el valor calculado de \(V\) con un valor crítico, y si \(V\) es mayor que este valor crítico (\(c\)), rechazamos la hipótesis nula.

Al igual que antes, el cálculo del valor-\(p\) se estima como \(1-F_{m-1,n-1}(V)\), donde \(F_{m-1,n-1}\) es la función de distribución acumulada de la distribución \(F\) con \(m-1\) y \(n-1\) grados de libertad, y \(V\) es el valor calculado del estadístico.

Ejemplo 12.5 Suponga que se tienen observaciones normales independientes de la forma \(X_1,\dots,X_{6}\sim N(\mu_1,\sigma_1^2)\), \(s_X ^2 =\frac{30}{6-1}=6\), \(Y_1,\dots,Y_{21}\sim N(\mu_2,\sigma_2^2)\), \(s_Y^2=\frac{40}{21-1}=2\).

Definamos la hipótesis nula como \(H_0: \sigma_1^2\leq \sigma_2^2\) y la hipótesis alternativa como \(H_1: \sigma_1^2> \sigma_2^2\). Tome \(\alpha_0 = 5\%\).

Calculamos \(V = \dfrac{30/5}{40/20} = 3\) y \(F^{-1}_{5,20}(1-0.05) = 2.71.\)

En este caso debemos rechazar \(H_0\) pues \(V\geq c\) o lo que es equivalente \(3 \geq 2.71\).

El valor-\(p\) corresponde a \(1-G_{5,20}(3) = 0.035.\)

Si \(\alpha_0 = 1\%\), no rechazo. Si \(\alpha_0 = 5\%\) rechazo.

Ejemplo 12.6 Ejemplo: Suponga que se tienen los siguientes datos

m <- 20
X <- rnorm(n = m, mean = 0, sd = sqrt(6))
head(X)

[1]  2.0924412  0.7803453  5.2993824 -2.3160857  1.0543316 -3.8058495

n <- 40
Y <- rnorm(n = n, mean = 10, sd = sqrt(2))
head(Y)

[1]  9.812901 11.088521 10.556011 12.085797 10.805107 12.329180

Es decir tener 20 datos normales con \(\sigma_1^2 = 6\) y 40 datos normales con \(\sigma_2^2 = 2\).

En todo caso asuma que \(\sigma\) es desconocido para cada caso y solo tenemos los datos. Además queremos hacer la prueba de hipótesis

\[ \begin{array}{ll} H_{0}: & \sigma_{1}^{2} \leq \sigma_{2}^{2} \\ H_{1}: & \sigma_{1}^{2}>\sigma_{2}^{2} \end{array} \]

OJO: Según la forma que planteamos el ejercicio, deberíamos de rechazar \(H_0\) ya que \(\sigma_1^2 = 6 > 2 = \sigma_2^2\)

Calculamos el estadístico \(V\)

(s2_x <- var(X))

[1] 5.229209

(s2_y <- var(Y))

[1] 2.354692

(V <- s2_x / s2_y)

[1] 2.220761

Para calcular un cuantil te tamaño \(1-\alpha = 0.95\) se usa la siguiente función

(qnt <- qf(p = 1 - 0.05, df1 = m - 1, df2 = n - 1))

[1] 1.85992

¿Rechazamos \(H_0\)?

V > qnt

[1] TRUE

y el valor-\(p\) de la prueba es

1 - pf(q = V, df1 = m - 1, df2 = n - 1)

[1] 0.01730554

Interpretación: Rechazamos la hipótesis que \(\sigma_{1}^{2} \leq \sigma_{2}^{2}\) con un valor-\(p\) de 0.02.

12.2.1 Prueba de 2 colas (prueba de homocedasticidad)

Consideremos el problema de probar si las varianzas de dos poblaciones normales son iguales. Definimos la hipótesis nula (\(H_0\)) como \(\sigma^2_1=\sigma^2_2\) y la hipótesis alternativa (\(H_1\)) como \(\sigma^2_1\ne\sigma^2_2\).

Para tomar una decisión sobre si rechazar o no la hipótesis nula, utilizamos una estadística de prueba \(V\), que es la razón de las varianzas de las dos muestras. Rechazamos \(H_0\) si \(V\geq c_2\) o \(V\leq c_1\), donde \(c_1\) y \(c_2\) son los puntos de corte tales que

\[ P[V\leq c_1] = \frac{\alpha_0}{2} \quad \text{y} \quad P[V\geq c_2] = \frac{\alpha_0}{2} \]

Esto se traduce en que \(c_1 = F_{m-1,n-1}^{-1}\left(\frac{\alpha_0}{2}\right)\) y \(c_2 = F_{m-1,n-1}^{-1}\left(1-\frac{\alpha_0}{2}\right)\).

Bajo las hipótesis \(H_0: \sigma^2_1=\sigma^2_2\) vs \(H_1: \sigma^2_1\ne\sigma^2_2\), se rechaza si \(V\geq c_2\) o \(V\leq c_1\) con \(c_1,c_2\) tales que

\[\mathbb P[V\leq c_1] = \dfrac{\alpha_0}{2} \text{ y } \mathbb P[V\geq c_2] = \dfrac{\alpha_0}{2} \implies c_1 = F_{m-1,n-1}^{-1}\left(\dfrac{\alpha_0}{2}\right) \text{ y } c_2 = F_{m-1,n-1}^{-1}\left(1-\dfrac{\alpha_0}{2}\right)\]

Ejemplo 12.7 Retomemos el ejemplo de las nubes. Acá queremos probar si las varianzas son iguales o no. Es decir, queremos probar

\[ H_0: \sigma^{2}_{\text{con trat.}} = \sigma^{2}_{\text{sin trat.}} \quad vs \quad H_1: \sigma^{2}_{\text{con trat.}} \neq \sigma^{2}_{\text{sin trat.}} \]

(m <- length(con_tratamiento))

[1] 26

(n <- length(sin_tratamiento))

[1] 26

(s2_x <- var(con_tratamiento))

[1] 2.558444

(s2_y <- var(sin_tratamiento))

[1] 2.695663

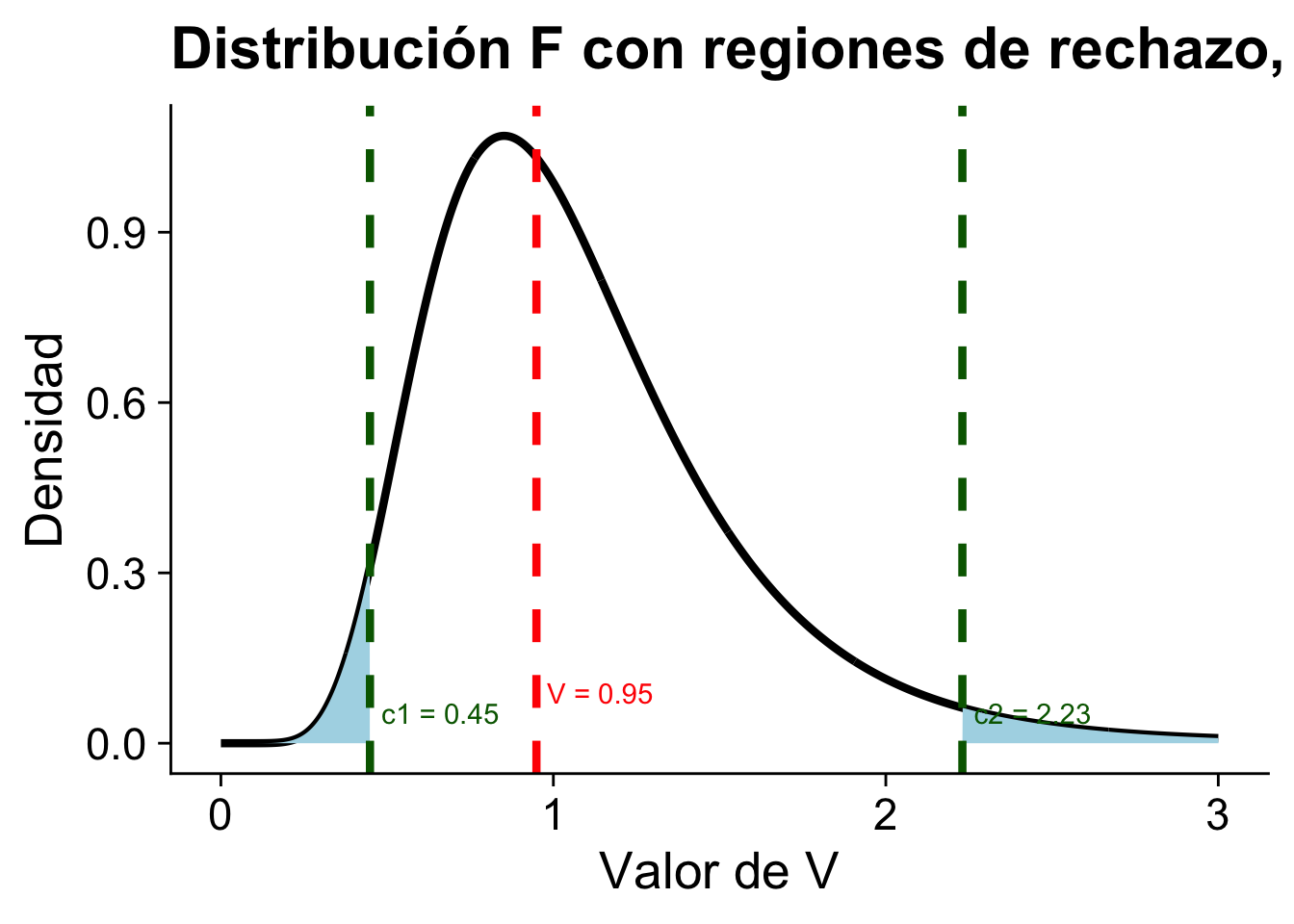
(V <- s2_x / s2_y)

[1] 0.9490963

El estadístico \(V\) es

\[V = \dfrac{\dfrac{63.96}{25}}{\dfrac{67.39}{25}} = 0.9491\]

Se tiene que \(c_1 = F^{-1}_{25,25}(0.0025) = 0.4484\) y \(c_2 = F^{-1}_{25,25}(0.975) = 2.23\).

(c1 <- qf(0.025, df1 = m - 1, df2 = n - 1))

[1] 0.4483698

(c2 <- qf(0.975, df1 = m - 1, df2 = n - 1))

[1] 2.230302

Podemos rechazar \(H_0\) si \(V\geq c_2\) o \(V\leq c_1\)

V < c1

[1] FALSE

V > c2

[1] FALSE

Ahora el resultado nos dice que no podemos rechazar \(H_0\) ya que \(V = 0.9491\) y \(c_1 = 0.4484\) y \(c_2 = 2.23\). Es decir, no hay evidencia suficiente para decir que las varianzas son diferentes.

Si observamos \(V=v\), podemos rechazar si
\[ v\leq F^{-1}_{m-1,n-1}\left(\dfrac{\alpha_0}2\right) \implies 2F_{m-1,n-1}(v)\leq \alpha_0 \]

o tambien si

\[v\geq F^{-1}_{m-1,n-1}\left(1-\dfrac{\alpha_0}2 \right) \implies F_{m-1,n-1}(v) \geq 1-\dfrac{\alpha_0}2 \implies \alpha_0\geq 2(1-F_{m-1,n-1}(v)) \]

Por lo tanto, el valor-\(p\) es \[\text{valor-}p = 2\min[1-F_{m-1,n-1}(v), F_{m-1,n-1}(v)]\]

2 * min(1 - pf(q = V, df1 = m - 1, df2 = n - 1),
        pf(q = V, df1 = m - 1, df2 = n - 1))

[1] 0.8971154

Interpretación: La prueba de hipótesis no rechaza la hipótesis de homocedasticidad con un nivel de confianza del 5%.

Propiedad. La prueba \(F\) es un LRT.

Smith, Howard L., Neill F. Piland, y Nancy Fisher. 1992. «A Comparison of Financial Performance, Organizational Characteristics and Management Strategy Among Rural and Urban Nursing Facilities». The Journal of Rural Health 8 (1): 27-39. https://doi.org/10.1111/j.1748-0361.1992.tb00324.x.