3 Inferencia estadística

Definición 3.1 (Modelo estadístico) Un modelo estadístico es una representación matemática que nos ayuda a entender y analizar fenómenos aleatorios. Para construir un modelo estadístico, es esencial identificar ciertos elementos clave. A continuación, se describen estos elementos:

La relación entre una variable observable $X_t$ y una hipotéticamente observable $Y_t$ se puede expresar como:

\[\begin{equation*} \underbrace{X_t}_{\text{Observable}} = \underbrace{Y_t}_{\text{Hip. observable}} + \underbrace{\epsilon}_{\text{Ruido}} \end{equation*}\]

Aquí:
- $X_t$: Es la variable que realmente observamos.
- $Y_t$: Representa el valor “verdadero” o real del fenómeno que estamos analizando.
- $\epsilon$: Es el ruido o error, que captura la aleatoriedad no asociada directamente con el fenómeno. Puede surgir debido a errores de medición, cambios en condiciones externas, entre otros. Es importante notar que, en la práctica, ni $Y_t$ ni $\epsilon$ pueden ser conocidos con precisión. Por lo tanto, $X_t$ es nuestra mejor representación del fenómeno.
Distribución conjunta de una muestra de variables observables.

Este elemento se refiere al conjunto de supuestos que estamos utilizando para describir y analizar nuestras observaciones.
Parámetros que son hipotéticamente observables (desconocidos).

Estos parámetros nos ayudan a calibrar el modelo de manera que se ajuste de la mejor manera posible a los datos observados. En otras palabras, ¿cómo podemos ajustar los componentes del modelo para que refleje de cerca la realidad? Al final queremos hacer una versión basada en los datos observados del parámetro teórico.
La especificación de la distribución de ese parámetro. consiste en una identificación de variables aleatorias
- En el enfoque frecuentista: Se utiliza para determinar intervalos de confianza y realizar pruebas de hipótesis.
- En el enfoque bayesiano: Los parámetros no son simplemente valores fijos, sino que se consideran como distribuciones completas.

Observación. Una estimador de un parámetro $\theta$ es una variable aleatoria ya que se construye a partir de los datos. Es esencial tener en cuenta su distribución condicionada a los datos observados.

3.1 Tipos de inferencia estadística

Una inferencia estadística no tiene el mismo objetivo siempre. Es decir, dependiendo del objetivo que busquemos, nos gustaría entender una parte diferente del fenómeno que estamos estudiando.

En particular podemos definir 3 muy claramente.

Definición 3.2 (Tipos de inferencia estadística) Dependiendo del objetivo que busquemos, entonces le tipo de inferencia será diferente:

La inferencia estadística puede tener diferentes objetivos. Algunos de los más comunes son:

Predicción: Se trata de predecir valores futuros $X_{n+1}, X_{n+2}, \dots$ basándonos en observaciones pasadas $X_1, \ldots, X_n$. Si lo que queremos predecir es un parámetro de una distribución, entonces nos referimos a este proceso como estimación.
Problemas de Decisión Estadística: Después de analizar la muestra, podemos usar otras técnicas para tomar decisiones sobre el parámetro. Por ejemplo, determinar qué tan cerca está nuestro estimador del valor real o si, con cierto nivel de confianza, nuestro estimador supera un valor específico.
Diseños Experimentales: Usando herramientas inferenciales, podemos determinar cuántos sujetos o unidades experimentales necesitamos para obtener un cierto grado de confianza en nuestros resultados.

3.2 Elementos de un modelo estadístico

Es esencial entender que las variables aleatorias provienen de fenómenos o eventos específicos. En estadística, a menudo nos referimos a estas variables como muestras o datos. A continuación, se describen los elementos clave que componen un modelo estadístico.

Definición 3.3 (Muestra o Datos) Una muestra o conjunto de datos se refiere a una secuencia de variables aleatorias independientes, denotadas como $X_1,X_2,\dots, X_n,\dots$ que describen un fenómeno particular. Estas variables tienen una distribución que, en muchos casos, es desconocida.

Definición 3.4 (Inferencia estadística) La inferencia estadística es un proceso que nos permite hacer afirmaciones basadas en probabilidades sobre ciertas partes o la totalidad de un modelo estadístico.

Uno de los elementos más importantes en la inferencia son los parámetros.

Definición 3.5 (Parámetro/Espacio paramétrico) Un parámetro es una característica o conjunto de características que determinan la distribución conjunta de las variables aleatorias que estamos estudiando. El conjunto total de estos parámetros se denomina espacio paramétrico, y se denota como $\Omega$.

Definición 3.6 (Estadístico) Si consideramos variables aleatorias observables $X_1, \ldots, X_n$ y $r$ es una función arbitraria de valores reales de $n$ variables reales. Entonces la variable aleatoria $T=r\left(X_1, \ldots, X_n\right)$ se llama estadístico.

Observación. Ejemplos comunes de estadísticos que ustedes conocen son el promedio, la mediana, la varianza, los cuantiles, etc.

Ejemplo 3.1 (Componentes electrónicos) Consideremos un componente electrónico y queremos determinar cuánto tiempo tarda en fallar. Para abordar esta pregunta, podemos descomponerla en varias partes:

Variable Aleatoria: Suponemos que los tiempos de vida observados del componente son aleatorios.
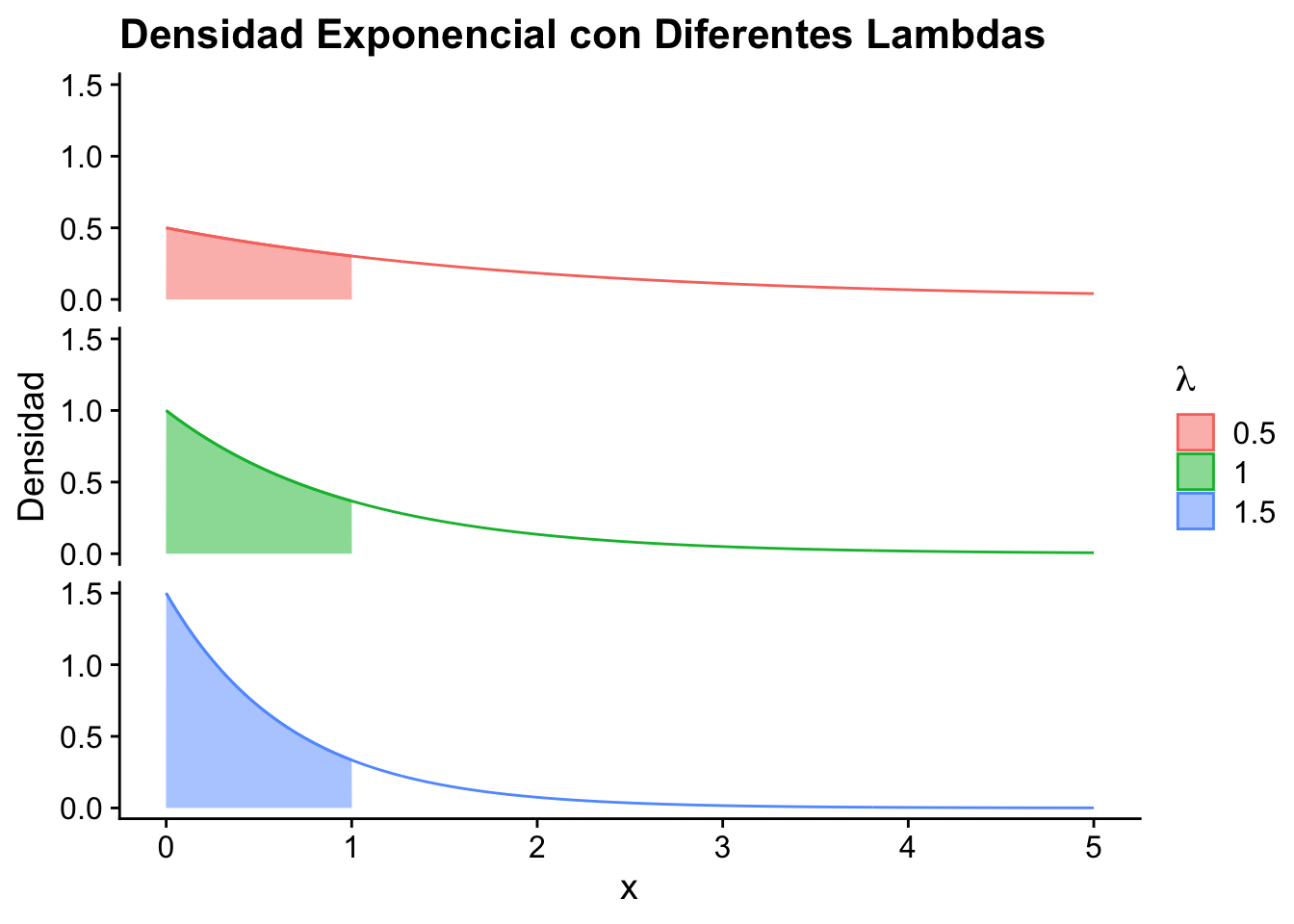
Distribución: Una distribución adecuada para modelar este fenómeno podría ser la exponencial, dado que entre más tiempo en uso tiene el componente mayor es la probabilidad de que deje de funcionar.
Parámetro: Definimos un valor $\theta>0$, que representa la tasa de fallo (en unidades de 1/Tiempo, por ejemplo, años).
Estadístico: Si tomamos una muestra de tiempos de vida del componente, podemos calcular el promedio de estos tiempos. Este promedio es un estadístico que nos da una idea de la tasa de fallo del componente.
Distribución del Parámetro: Podemos emplear técnicas para determinar cómo se distribuye el estadístico del parámetro $\theta$, como intervalos de confianza y pruebas de hipótesis. La importancia de este parámetro recae en que muestra la “rapidez” con la que se da el tiempo de fallo.

En resumen, estamos utilizando un modelo exponencial y suponemos que toda la información relevante está contenida en el parámetro $\theta$. Con esta información, podemos hacer inferencias sobre el modelo.

Es decir, tenemos un modelo (exponencial) y estamos decretando que su información estará concentrada en el parámetro $\theta$. Además, con esa información podemos hacer preguntas inferencial al modelo.

Observación. Note que en el caso anterior el parámetro $\theta$ contiene la información del modelo.

Una forma de resumir 1., 2. y 3. es decir, que se toma una muestra \[\begin{equation*} X_1,X_2,\dots, X_n,\dots \stackrel{i.i.d}{\sim} \text{Exp}(\theta). \end{equation*}\]

El estadístico se puede estimar de muchas formas. Es decir, este representa un resumen que dependiendo del tipo de técnica que se utilice, podemos obtener diferentes resultados.

Ejemplo 3.2 (Componentes electrónicos) Siguiendo con el Ejemplo 3.1 Para estimar el parámetro $\theta$ en este curso estudiaremos dos formas: Frecuentista o Bayesiana.

Frecuentista: En este enfoque, asumimos que $\theta$ es una constante y utilizamos técnicas estándar para estimarla. Por ejemplo, si $\mathbb{E}(X) = \dfrac{1}{\theta}$, sabemos que $X \sim \text{Exp}(\theta)$. Por la Ley de Grandes Números, podemos usar la media muestral $\overline{X}_n$ como un estimador para $\theta$. \[\begin{equation*} \underbrace{\dfrac{1}{n} \sum_{i=1}{X_i}}_{\bar{X}_n} \xrightarrow[n\to \infty]{\mathbb{P}}\mathbb{E}(X) = \dfrac{1}{\theta} \end{equation*}\] por propiedad de convergencia en probabilidad. Un posible candidato para el estadístico de $\theta$ es $\dfrac{1}{\bar X_n}$, bajo el supuesto por Ley de los Grandes Números que, $\theta$ es un valor una constante.
Bayesiano: En este enfoque, no asumimos que $\theta$ no necesariamente es determinístico (i.e, que solo tiene un valor fijo). Esto debido a factores externos o por la naturaleza del fenómeno. En lugar de asumir un estadístico determinado para $\theta$, asumimos que tiene la forma de un modelo probabilístico de la forma (tasa siempre positiva): \[\begin{equation*} \theta \sim \Gamma(\alpha_0,\beta_0) \end{equation*}\] Luego, según la experiencia previa , se puede esperar la tasa esperada de fallo de 0.5/año. Por lo tanto se puede estimar el parámetro como \[\begin{equation*} \mathbb{E}(\theta) = \dfrac{1}{2} = \dfrac{\alpha_0}{\beta_0}. \end{equation*}\] Según la distribución gamma, se puede establecer como primer indicio de que $\alpha_0 = 1$ y de $\beta_0 = 2$.

3.3 Ejemplos típicos de inferencia estadística frecuentista y bayesiana

Para finalizar este capítulo, presentamos algunos ejemplos típicos donde se aplican técnicas de inferencia estadística. Esto visto del punto de vista frecuentista y bayesiano.

Ejemplo 3.3 (Estimación del promedio de una población) Supongamos que queremos estimar el promedio de altura de todos los estudiantes de una universidad a partir de una muestra aleatoria.

Datos: Alturas de una muestra aleatoria de 100 estudiantes: $X_1, X_2, \dots, X_{100}$.
Estimador: La media muestral $\bar{X}$ es un estimador insesgado del promedio poblacional $\mu$. \[ \bar{X} = \frac{1}{100} \sum_{i=1}^{100} X_i \]
Intervalo de Confianza: Para un nivel de confianza del 95%, el intervalo de confianza para $\mu$ es: \[ \bar{X} \pm 1.96 \times \frac{\sigma}{\sqrt{100}} \] donde $\sigma$ es la desviación estándar de la muestra.
Prueba de Hipótesis: Supongamos que queremos probar la hipótesis de que el promedio de altura de los estudiantes es mayor a 1.70 m. Entonces, nuestra hipótesis nula es: $H_0: \mu \leq 1.70$. Para probar esta hipótesis, podemos usar la media muestral $\bar{X}$ y el estadístico de prueba: \[ Z = \frac{\bar{X} - 1.70}{\sigma / \sqrt{100}} \] Si $Z > 1.96$, entonces rechazamos la hipótesis nula. En caso contrario, no podemos rechazarla.

Ejemplo 3.4 (Estimación de la proporción de estudiantes que aprueban) Queremos estimar la proporción de estudiantes que aprueban un examen, pero ya tenemos información de años anteriores.

Datos: Supongamos que de 100 estudiantes que tomaron el examen este año, 70 aprobaron. Es decir $X=70$.
Prior: Basado en años anteriores, suponemos que la proporción de aprobados sigue una distribución beta con parámetros $\alpha = 60$ y $\beta = 40$. Esto podría representar, por ejemplo, una creencia previa de que alrededor del 60% de los estudiantes aprueban el examen cada año. \[ p \sim Beta(\alpha, \beta) \]
Verosimilitud: La verosimilitud, basada en los datos de este año, se modela con una distribución binomial, donde $ n = 100 $ es el número total de estudiantes y $ p $ es la proporción desconocida de estudiantes que aprueban. \[ L(p|X) = \binom{n}{X} p^X (1-p)^{n-X}. \]
Posterior: Usando el teorema de Bayes, la distribución posterior es proporcional al producto de la verosimilitud y el prior: \[ f(p|X) \propto L(p|X) \times f(p) \] Dado que estamos combinando una distribución beta con una binomial, la posterior también será una distribución beta, pero con parámetros actualizados: \[ p|X \sim Beta(\alpha + X, \beta + n - X) = Beta(130, 70) \]
Factor de Bayes: El factor de Bayes compara la verosimilitud de los datos bajo dos hipótesis. Supongamos que nuestra hipótesis nula es que la proporción de aprobados es 0.5 y la alternativa es cualquier otro valor. El factor de Bayes se calcula como: \[ B = \frac{L(p=0.5|X)}{\int L(p|X) f(p) dp} \] Si $ B > 1 $, los datos favorecen la hipótesis alternativa. Si $ B < 1 $, favorecen la hipótesis nula.
Intervalo de Credibilidad: El intervalo de credibilidad del 95% para la proporción de aprobados, basado en la distribución posterior, se puede calcular usando percentiles de la distribución beta. Para nuestro ejemplo, el intervalo de credibilidad del 95% sería, (0.58, 0.71), lo que indica que, basándonos en los datos y la información previa, estamos 95% seguros de que la proporción real de estudiantes que aprueban está entre 0.58 y 0.71.