10 Pruebas de hipótesis

La prueba de hipótesis es un procedimiento estadístico fundamental que permite tomar decisiones con respecto a la veracidad de afirmaciones sobre parámetros poblacionales basándose en datos muestrales. A través de este capítulo, exploraremos el procedimiento de las pruebas de hipótesis utilizando un caso práctico relacionado con la inducción de lluvia mediante la inyección de nitrato de plata en nubes.

Ejemplo 10.1 Suponga que se hace un experimento donde se seleccionan 52 nubes al azar y 26 se les inyecta nitrato de plata y a las otras 26 no. Entonces se quiere saber cuál de los dos grupos produce más lluvia.

Los datos de la cantidad de lluvia para este experimento se encuentran en el archivo clouds.txt y se pueden cargar con el siguiente código:

nubes <- read.table(file = "./data/clouds.txt", sep = "\t", header = TRUE)

Unseeded.Clouds	Seeded.Clouds
1202.6	2745.6
830.1	1697.8
372.4	1656.0
345.5	978.0
321.2	703.4
244.3	489.1

Para una interpretación más sencilla de los datos, transformaremos la cantidad de lluvia a una escala logarítmica:

lognubes <- log(nubes)

Unseeded.Clouds	Seeded.Clouds
7.092241	7.917755
6.721546	7.437089
5.919969	7.412160
5.844993	6.885510
5.772064	6.555926
5.498397	6.192567

Visualizaremos la distribución de la cantidad de lluvia para cada grupo mediante histogramas:

df <- as.data.frame(nubes) %>%
  pivot_longer(
    cols = everything(),
    names_to = "tratamiento", values_to = "lluvia"
  ) %>%
  mutate(log_lluvia = log(lluvia))

ggplot(data = df) +
  geom_histogram(
    aes(
      x = lluvia,
      y = after_stat(density),
      fill = tratamiento
    ),
    color = "black", bins = 10
  ) +
  facet_wrap(. ~ tratamiento) +
  cowplot::theme_cowplot()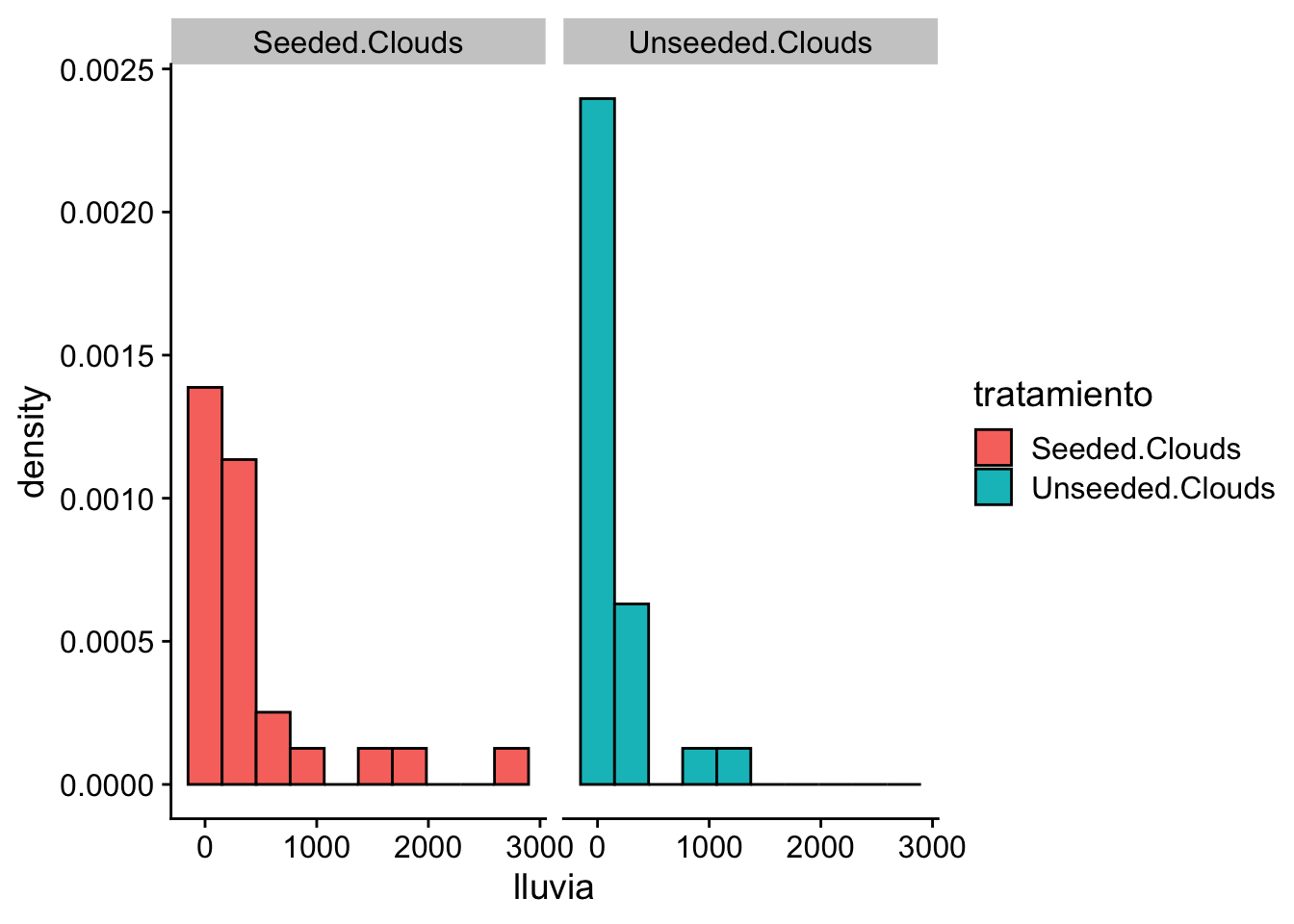

ggplot(data = df) +
  geom_histogram(aes(
    x = log_lluvia,
    y = after_stat(density),
    fill = tratamiento
  ), color = "black", bins = 10) +
  facet_wrap(. ~ tratamiento) +
  cowplot::theme_cowplot()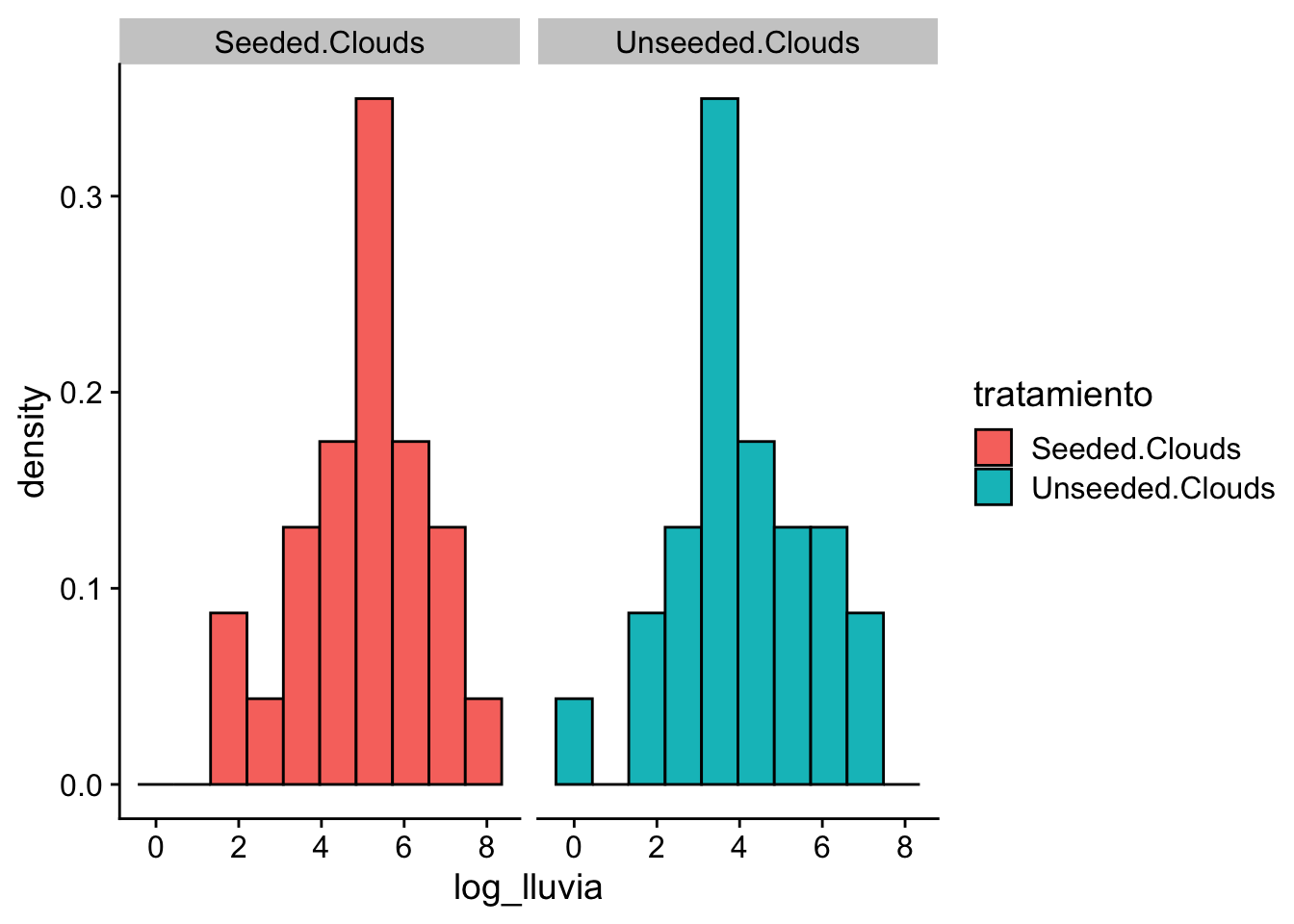

En este caso supondremos que la variable log_lluvia se puede modelar como una $N(\mu,\sigma^2)$, donde tanto $\mu$ y $\sigma$ son desconocidos.

Suponga que el investigador desea saber si $\mu>4$ en cualquier caso.

¿Por qué $\mu>4$?

Esto nace a partir de la pregunta de investigación y se fórmula cierto tipo de hipótesis con respecto a los datos.

En este caso sería $\theta = (\mu,\sigma^2)$, ¿Será cierto que para $\theta\in\{(\mu,\sigma^2):\mu>4\}$?

En el caso frecuentista, se tiene que $\Omega = \Omega_0 \cup\Omega_1$ conjuntos disjuntos tales que:

\[\begin{align*} H_0 : \text{hipótesis en donde }\theta \in \Omega_0.\\ H_1 : \text{hipótesis en donde }\theta \in \Omega_1.\\ \end{align*}\]

Objetivo

El objetivo es decidir si $H_0$ o $H_1$ es cierto, con los datos disponibles o lo que se conoce como el problema de pruebas de hipótesis.

Definición 10.1 Defina $H_0$ como la hipótesis nula y $H_1$ como la hipótesis alternativa. Una vez que se ha realizado una prueba de hipótesis si afirmamos $\theta \in \Omega_1$ decimos que rechazamos $H_0$. Si $\theta \in \Omega_0$, decimos que no rechazamos $H_0$¹.

¹ Esto no quiere decir que aceptamos $H_0$. En general, lo correcto es decir que no tenemos suficiente evidencia estadística para rechazar $H_0$.

Definición 10.2 Suponga que $X_1,\dots, X_n\sim f(x|\theta)$, $\theta \in \Omega$, $\Omega = \Omega_0 \cup\Omega_1$ y queremos probar la hipótesis $H_0: \theta \in \Omega_0$, $H_1: \theta \in \Omega_1$. Entonces para $i=0,1$, se definen los siguientes conceptos:

Si $\Omega_i$ tiene solamente un valor de $\theta$, $H_i$ es una hipótesis simple.
Si $\Omega_i$ tiene más de un valor de $\theta$, $H_i$ es una hipótesis compuesta.
Decimos que tenemos una hipótesis compuestas de una cola en el caso de que
1. Si $\Omega_0 = [\theta_0, +\infty]$, entonces $H_0: \theta\geq \theta_0$ y $H_1: \theta <\theta_0$.
2. Si $\Omega_0 = (-\infty,\theta_0]$, $H_0: \theta\leq \theta_0$ y $H_1: \theta>\theta_0$.
Si $H_1: \theta \ne \theta_0$ y $H_0: \theta = \theta_0$ es una hipótesis de 2 colas.

10.1 Regiones críticas y estadísticas de prueba

En esta sección se introducen los conceptos de región crítica y estadística de prueba. Los conceptos son algo técnicos, por lo que primero se introducen con un ejemplo sencillo.

Ejemplo 10.2 Supongamos que queremos adivinar un número aleatorio. Ahora, los números que se nos presentan provienen de un generador de números normales, con media $\mu$ desconocida y varianza $\sigma^2$ conocida. Formalmente sería $X_1,\dots, X_n \sim N(\mu,\sigma^2)$, $\mu$ desconocido, $\sigma^2$ conocido.

Se gana el juego el que logre adivinar el valor de $\mu$.

Supongamos que se le presenta un número inicial, $\mu_0$, y se le pide que decida si este número es igual que la media $\mu$. Es decir, queremos probar si $H_0: \mu = \mu_0$ vs $H_1: \mu\neq \mu_0$.

La lógica nos dice que rechazamos $H_0$ si $\mu$ está “muy alejado” de $\mu_0$.

¿Cómo definimos “muy alejado”? Una forma es verificar si el número inicial está “muy lejos” de la cantidad promedio de tu grupo de números. Elegirás un número ‘c’, y si la diferencia entre la cantidad promedio de tu grupo de números y el número inicial es mayor que ‘c’, entonces rechazarás la hipótesis.

Para hacer más concreto esta idea, seleccionemos un número $c>0$ tal que si $|\bar X_n -\mu_0|>c$.

Si tenemos una muestra $X_1,\dots,X_n \sim f(x|\theta)$, solo estamos observado una realización de la muestra. Entonces, dividamos nuestra información total del problema en dos partes (conjuntos disjuntos):

$S_0\subset \mathcal X$: conjunto de datos observados en donde no se rechaza $H_0$ y
$S_1\subset \mathcal X$: conjunto de datos observados en donde se rechaza $H_0$.

Nota

A $S_1$ se le llama región crítica o región de rechazo de la prueba de hipótesis.

En el caso en que se rechaza $H_0$ si $T>c$ con $T = |\bar X_n-\mu_0|$ estadístico de prueba y $(c,\infty)$ es la región de rechazo.

Imagina que estás realizando este experimento muchas veces, recogiendo grupos de números y calculando la diferencia entre la cantidad promedio de cada grupo y el número inicial. Cada vez que esta diferencia es mayor que ‘c’, marcas ese evento como TRUE.

Para un primer ejemplo supongamos que decidimos que $\mu_0 =2$.

mu_0 <- 2

x <- matrix(rnorm(1000 * 1000, mean = 2, sd = 3), ncol = 1000)
head(x[,1:3])

           [,1]       [,2]       [,3]
[1,]  0.4439311  5.3318593  2.7846568
[2,]  0.6921997  6.0572891  3.9763594
[3,] -1.9680055  2.8321079 -4.4572448
[4,]  4.6078036  5.6852064 -0.9708600
[5,]  5.7628723 -0.2060804  0.1280562
[6,]  5.1858587 -1.0399103  2.2288318

x_bar <- apply(x, 2, mean)
head(x_bar)

[1] 2.034713 1.870869 1.807950 2.042236 2.361794 1.993962

t_est <- abs(x_bar - mu_0)
head(t_est)

[1] 0.034713376 0.129131033 0.192049879 0.042235768 0.361794352 0.006038227

c <- seq(-0.25, 0.5, length.out = 1000)
head(c)

[1] -0.2500000 -0.2492492 -0.2484985 -0.2477477 -0.2469970 -0.2462462

df <- data.frame(c = numeric(), test = logical(), region = character())
for (k in 1:length(c)) {
  df <- rbind(df, data.frame(
    c = c[k],
    test = mean(t_est >= c[k]), region = "S_1"
  ))
}

df <- rbind(df, data.frame(c, test = 1 - df$test, region = "S_0"))
df[500:503,]

            c  test region
500 0.1246246 0.199    S_1
501 0.1253754 0.196    S_1
502 0.1261261 0.195    S_1
503 0.1268769 0.194    S_1

df[1500:1503,]

             c  test region
1500 0.1246246 0.801    S_0
1501 0.1253754 0.804    S_0
1502 0.1261261 0.805    S_0
1503 0.1268769 0.806    S_0

ggplot(df, aes(x = c, y = test, color = region)) +
  geom_line(linewidth = 2) +
  ylab("Promedio de veces donde T >= c") +
  theme_minimal()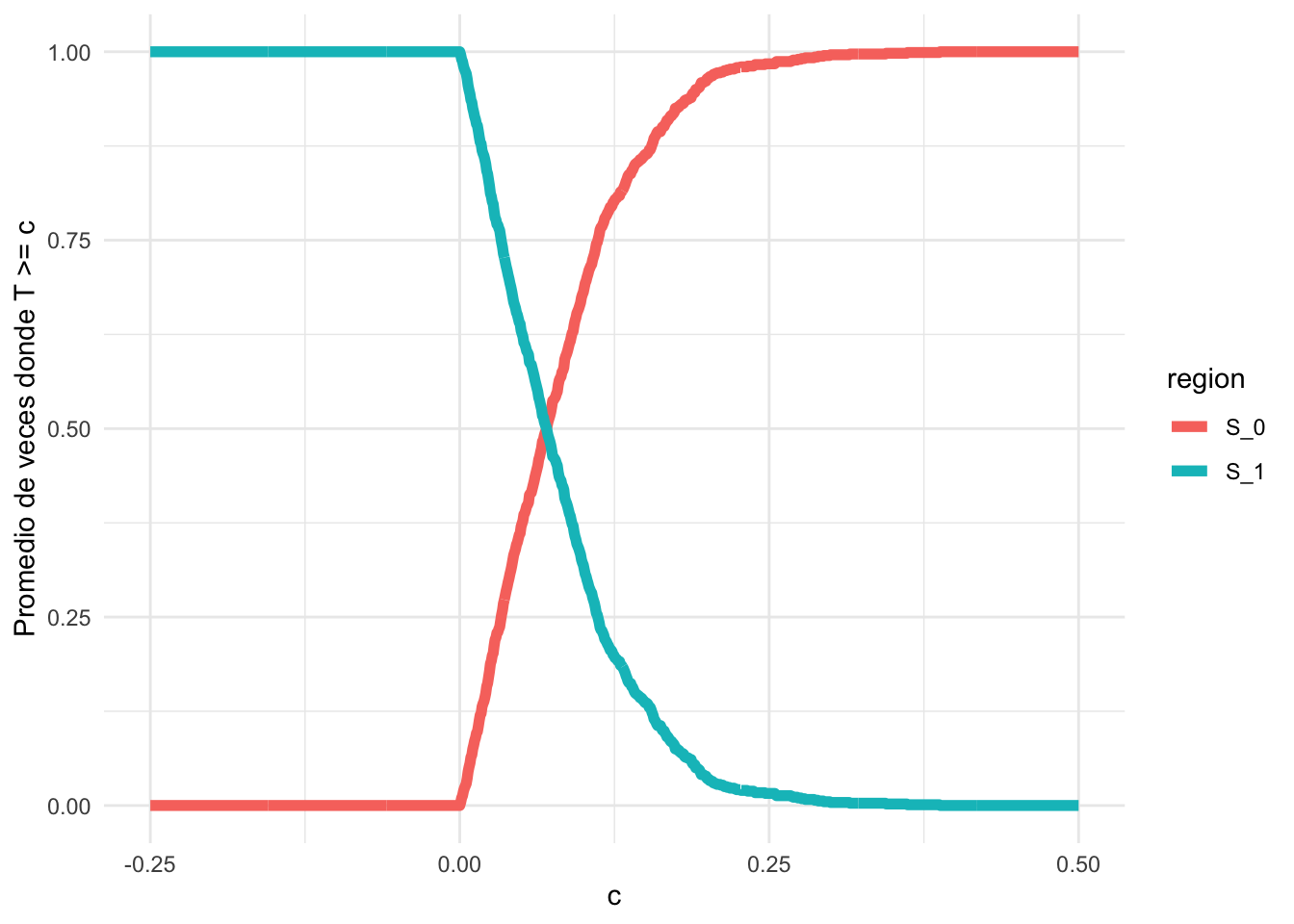

Si graficamos el promedio de estas marcas en función de diferentes valores de ‘c’, obtendremos una curva que empieza en algún valor y luego disminuye. Este punto de partida será cerca de 0, lo que significa que hasta ese valor, estás en la región crítica o de rechazo. Después de ese valor, la región crítica se hace cada vez más pequeña, porque la diferencia $\vert \bar{X} - \mu \vert \approx 0$.

Ahora, ¿qué pasaría si cambiamos el número inicial a $\mu = 4$?

mu_0 <- 4
t_est <- abs(x_bar - mu_0)

c <- seq(-0.25, 3, length.out = 1000)

df <- data.frame(c = numeric(), test = logical(), region = character())
for (k in seq_along(c)) {
  df <- rbind(
    df,
    data.frame(c = c[k], test = mean(t_est >= c[k]), region = "S_1")
  )
}

df <- rbind(df, data.frame(c, test = 1 - df$test, region = "S_0"))

ggplot(df, aes(x = c, y = test, color = region)) +
  geom_line(linewidth = 2) +
  ylab("Promedio de veces donde T >= c") +
  theme_minimal()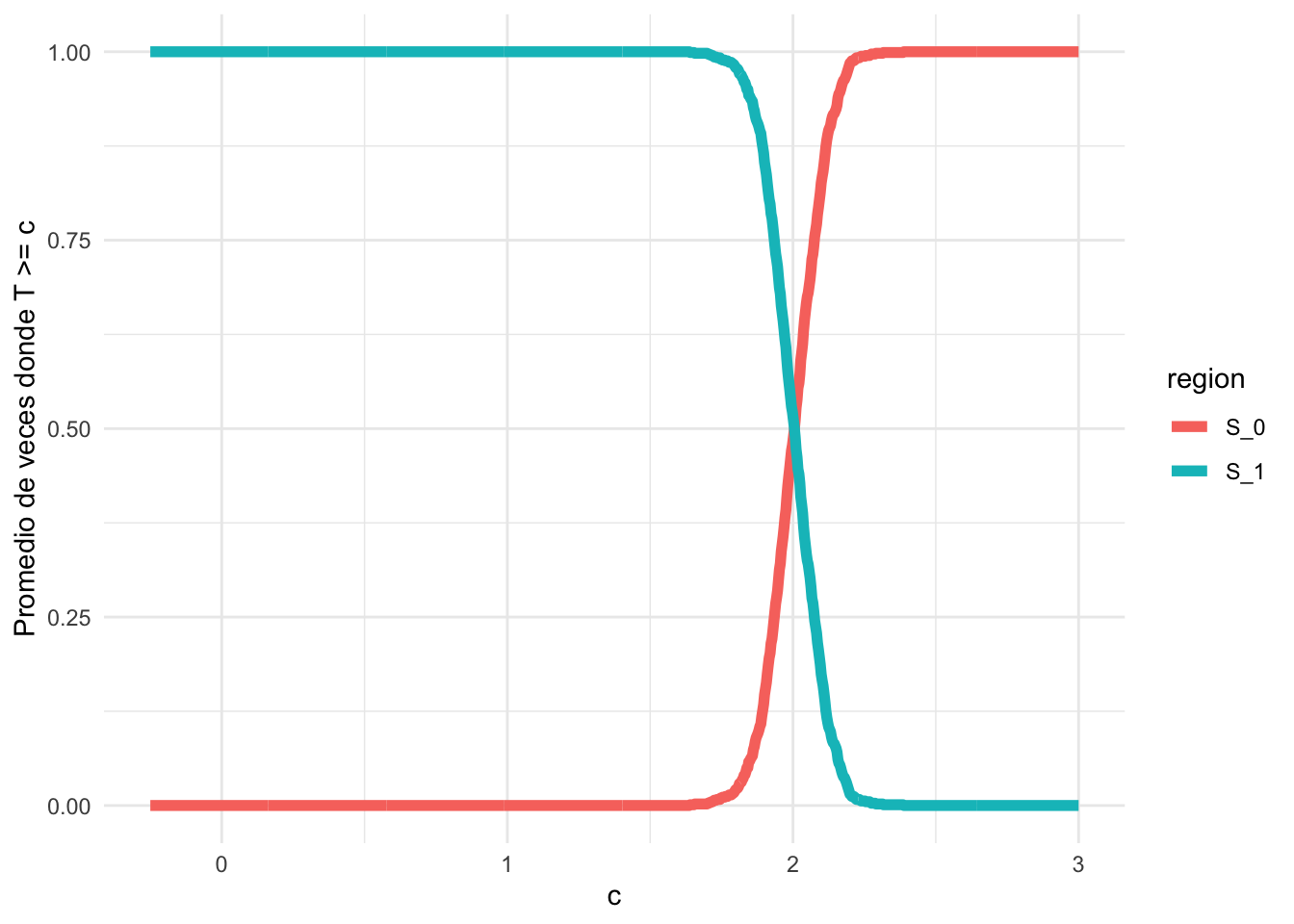

Si haces el mismo experimento y trazas la misma gráfica, notarás que el punto de partida de la curva ahora se ha movido a un valor cercano a 2. Eso significa que tu región crítica ha cambiado.

Observación. En la mayoría de los casos, la región crítica se define en términos de un estadístico $T = r(x)$.

Definición 10.3 Sea $X$ una muestra aleatoria con distribución $f(x|\theta)$ y $T=r(X)$ un estadístico y $R\subset \mathbb R$. Suponga que se puede verificar las hipótesis al afirmar “rechazamos $H_0$ si $T\in R$”, entonces $T$ es un estadístico de prueba y $R$ es la región de rechazo de la prueba.

Ejemplo 10.3 (Continuación Ejemplo 10.1) Consideremos ahora el ejemplo de la lluvia, donde definimos las hipótesis de la siguiente manera:

\[ H_0: \mu \leq 4 \text{ versus } H_1: \mu > 4 \]

En este caso podríamos decir que rechazamos $H_0$ si la media empírica es “mayor” que 4 y no rechazamos $H_0$ si la media empírica es “menor” que 4.

Sin embargo, la ambigüedad se introduce con las palabras “mayor” y “menor”, ya que no son términos precisos. Para resolver este problema, tenemos dos opciones:

Construya la región de critica de la forma \[\begin{equation} S_{0}=\left\{\boldsymbol{x}:\leq \bar{X}_{n}-\mu_{0} \leq c\right\}, \quad \text { y } \quad S_{1}=S_{0}^{C}. \end{equation}\]

Luego podríamos observar cuál probabilidad que ocurre para cada valor de $c$. El problema con esta construcción es que requiere conocer todos los posibles vectores de datos $\mathbf{X}$ y construir los conjuntos $S_0$ y $S_1$.

Una mejor opción es tener un estadístico que cumpla dos condiciones:
1. Sencillo de calcular posiblemente suficiente, minimal y eficiente.
2. Con una distribución conocida y posiblemente sin parámetros.

En este contexto, el promedio muestral $\bar{X}_{n}$ resulta ser un buen candidato. Tiene propiedades deseables de suficiencia, minimalidad y eficiencia, y sabemos su distribución según lo estudiado en capítulos anteriores.

Recordemos la Sección 8.3, donde se estudió la definición de la distribución $t$-Student. En particular, podemos utilizar la siguiente transformación:

\[\begin{equation*} U = \frac{n ^{1/2} (\bar{X}_{n} - \mu_0)}{s_n} \sim t_{n-1} \end{equation*}\]

donde \[\begin{align*} \bar{X}_{n} &= \frac{1}{n} \sum_{i=1}^{n} X_i \\ s^2_n &= \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar{X}_{n})^2 \\ \end{align*}\]

Lo natural debería ser rechazar $H_{0}$ si $U$ es grande.

A continuación, se muestran los cálculos y la gráfica correspondiente:

colnames(lognubes)

[1] "Unseeded.Clouds" "Seeded.Clouds"

x_bar_1 <- mean(lognubes[, 1])
x_bar_2 <- mean(lognubes[, 2])
s_1 <- sd(lognubes[, 1])
s_2 <- sd(lognubes[, 2])

n <- dim(lognubes)[1]


(u_1 <- sqrt(n) * (x_bar_1 - 4) / s_1)

[1] -0.02979683

(u_2 <- sqrt(n) * (x_bar_2 - 4) / s_2)

[1] 3.615624

ggplot(
  data = data.frame(x = (c(-1, 4))),
  mapping = aes(x)
) +
  stat_function(
    fun = dt, args = list(df = n - 1),
    mapping = aes(color = "Distribucioń t-student"),
    linewidth = 2
  ) +
  geom_vline(
    mapping = aes(
      xintercept = u_1,
      color = "Nubes no tratadas"
    ), linetype = "longdash",
    linewidth = 2
  ) +
  geom_vline(
    mapping = aes(
      xintercept = u_2,
      color = "Nubes tratadas"
    ), linetype = "longdash",
    linewidth = 2
  ) +
  cowplot::theme_cowplot()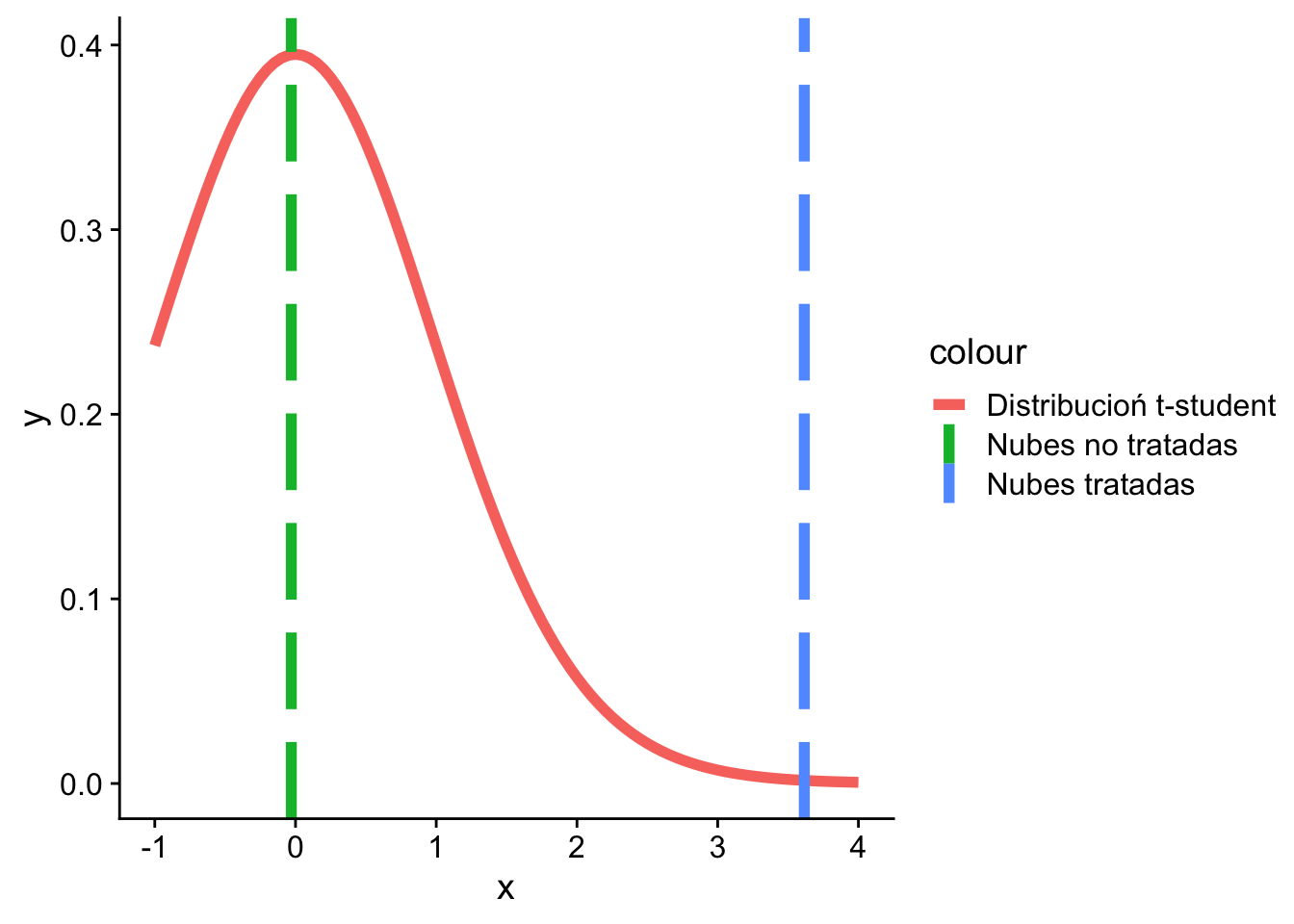

10.2 Función de potencia y tipos de error

Considérese un procedimiento de prueba, que llamaremos $\delta$. Este procedimiento debe estar basado en una región crítica o en un estadístico de prueba. Definimos la función de potencia de $\delta$, denotada como $\pi(\theta|\delta)$, como la probabilidad de rechazar la hipótesis nula $H_0$ dado el procedimiento de prueba $\delta$ para un valor $\theta$ en el conjunto $\Omega$.

Si $\delta$ utiliza una región crítica $S_1$, entonces la función de potencia se define como $\pi(\theta|\delta) = \mathbb P(X\in S_1|\theta)$ para cada valor de $\theta$ en $\Omega$.

Si $\delta$ se basa en un estadístico de prueba $T$ con una región de rechazo $R$, entonces la función de potencia se define como $\pi(\theta|\delta) = \mathbb P(T \in R|\theta)$ para cada valor de $\theta$ en $\Omega$.

Nota

La función de potencia ideal sería aquella donde $\pi(\theta|\delta) = 0$ si $\theta$ pertenece al conjunto de hipótesis nulas $\Omega_0$, y $\pi(\theta|\delta) = 1$ si $\theta$ pertenece al conjunto de hipótesis alternativas $\Omega_1$.

Ejemplo 10.4 Tomemos en cuenta el estadístico de prueba $T = |\bar X_n-\mu_0|$, con la región de rechazo $R = (c,\infty)$. Dado que $X_1,\dots, X_n$ siguen una distribución normal $N(\mu, \sigma^2)$, con $\mu$ desconocido y $\sigma^2$ conocido, la media muestral $\bar X_n$ también sigue una distribución normal $N\left(\mu,\dfrac{\sigma^2}{n}\right)$.

Podemos entonces definir la función de potencia de la siguiente manera:

\[\begin{align*} \pi(\theta\mid\delta) &= \mathbb P[T\in R\mid\mu] \\ & = \mathbb P [\vert\bar X_n -\mu_0\vert>c\mid\mu] \\ &= \mathbb P [\bar X_n > \mu_0+c\mid\mu] + \mathbb P [\bar X_n < \mu_0-c\mid\mu]\\ & = \mathbb P \left[\sqrt n \dfrac{(\bar X_n-\mu)}{\sigma}> \dfrac{(\mu_0+c-\mu)}{\sigma}\sqrt n \mid\mu\right] \\ & \qquad + \mathbb P \left[\sqrt n \dfrac{(\bar X_n-\mu)}{\sigma}< \dfrac{(\mu_0-c-\mu)}{\sigma}\sqrt n \mid\mu\right] \\ & = 1-\Phi\left(\sqrt n \dfrac{(\mu_0+c-\mu)}{\sigma} \right) + \Phi\left(\sqrt n \dfrac{(\mu_0-c-\mu)}{\sigma} \right) \end{align*}\]

A continuación, implementaremos la función de potencia en R y generaremos gráficos para visualizar su comportamiento.

# Definimos los parámetros
mu_0 <- 4
c <- 2
n <- 100
sigma <- 3

# Creamos una secuencia de valores mu
mu <- seq(0, 8, length.out = 1000)

# Calculamos la función de potencia
# para cada valor de mu
funcion_de_poder <- 1 -
  pnorm(sqrt(n) * (mu_0 + c - mu) / sigma) +
  pnorm(sqrt(n) * (mu_0 - c - mu) / sigma)

# Creamos un data.frame para visualizar los resultados
df <- data.frame(mu, funcion_de_poder,
  tipo = "Función de poder"
)
df <- rbind(df, data.frame(mu,
  funcion_de_poder = 1 - df$funcion_de_poder,
  tipo = "1 - Función de poder"
))

# Graficamos la función de potencia y su complemento
ggplot(df, aes(mu,
  funcion_de_poder,
  color = tipo
)) +
  geom_line(linewidth = 2) +
  theme_minimal()

# Creamos una matriz de combinaciones de mu y c
mu <- seq(0, 8, length.out = 100)
c <- seq(0, 4, length.out = 100)
mu_c <- expand.grid(mu, c)

# Calculamos la función de potencia para cada combinación de mu y c
funcion_de_poder_n_c <- 1 -
  pnorm(sqrt(n) * (mu_0 + mu_c[, 2] - mu_c[, 1]) / sigma) +
  pnorm(sqrt(n) * (mu_0 - mu_c[, 2] - mu_c[, 1]) / sigma)

# Graficamos la función de potencia en 3D
scatterplot3d::scatterplot3d(mu_c[, 2],
  mu_c[, 1],
  funcion_de_poder_n_c,
  type = "p", angle = 60,
  xlab = "c", ylab = "mu", zlab = "Función de poder"
)

10.2.1 Errores de Tipo I y Tipo II

En el contexto de las pruebas de hipótesis, podemos incurrir en dos tipos de errores:

Error de Tipo I: Se produce cuando rechazamos la hipótesis nula $H_0$ incorrectamente, es decir, cuando $\theta$ realmente pertenece a $\Omega_0$.
Error de Tipo II: Se produce cuando fallamos en rechazar la hipótesis nula $H_0$ incorrectamente, es decir, cuando $\theta$ realmente pertenece a $\Omega_1$.

Estos errores se pueden expresar en términos de la función de potencia:

Si $\theta \in \Omega_0$: $\pi(\theta|\delta)$ representa la probabilidad de un error de Tipo I.
Si $\theta \in \Omega_1$: $1-\pi(\theta|\delta)$ representa la probabilidad de un error de Tipo II.

Nota

En algunos libros se utiliza la siguiente notación:

$\beta$ = probabilidad de un error de Tipo II, conocido como un “falso negativo”
$1 − \beta$ = probabilidad de un “verdadero positivo”, es decir, rechazar correctamente la hipótesis nula. “1 − $\beta$” también se conoce como la potencia de la prueba.
$\alpha$ = probabilidad de un error de Tipo I, conocido como un “falso positivo”
$1 − \alpha$ = probabilidad de un “verdadero negativo”, es decir, no rechazar correctamente la hipótesis nula.

	$H_0$ es Verdadera	$H_0$ es Falsa
Probabilidad de rechazar $H_0$	$\alpha$	$1 - \beta$
Probabilidad de aceptar (no rechazar) $H_0$	$1 - \alpha$	$\beta$

El objetivo en las pruebas de hipótesis es minimizar tanto los errores de Tipo I como de Tipo II. Es decir, queremos que $\pi(\theta|\delta)$ sea pequeño cuando $\theta$ está en $\Omega_0$ y que $\pi(\theta|\delta)$ sea grande cuando $\theta$ está en $\Omega_1$.

Para lograr este equilibrio, se puede seleccionar un valor $\alpha \in (0,1)$ tal que

\[\pi(\theta|\delta) \leq \alpha\;\forall \theta\in\Omega_0 \tag{10.1}\]

Dentro de todas las pruebas que cumplen la condición anterior, seleccionamos aquella que maximice la potencia de la prueba para $\theta$ en $\Omega_1$.

Ejemplo 10.5 (Continuación del Ejemplo 10.4) En nuestro ejemplo suponga que elegimos $\alpha_{0} = 0.1$. La región roja indica donde estaría ubicado $\pi(\theta\vert \delta)\leq \alpha_{0}$.

La línea punteada negra indica el valor de 0.05.

ggplot() +
  geom_line(
    data = df,
    mapping = aes(x = mu, y = funcion_de_poder, color = tipo),
    linewidth = 2
  ) +
  geom_rect(
    data = data.frame(xmin = 0, xmax = 8, ymin = 0, ymax = 0.10),
    mapping = aes(xmin = xmin, xmax = xmax, ymin = ymin, ymax = ymax),
    alpha = 0.5, fill = "red"
  ) +
  geom_hline(yintercept = 0.05, linetype = "dotted", linewidth=2) +
  cowplot::theme_cowplot()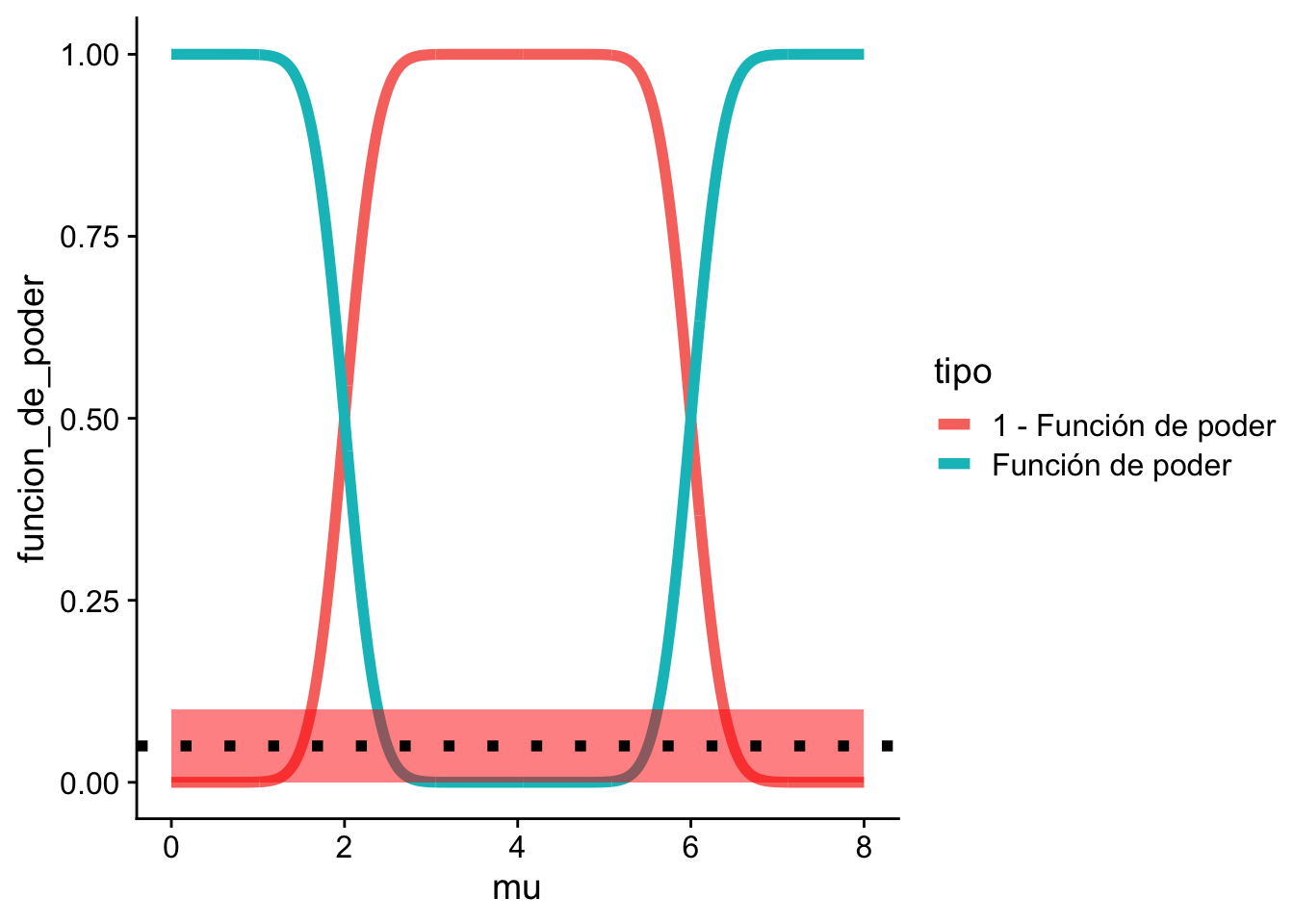

Otra estrategia para equilibrar los errores de Tipo I y Tipo II en una prueba de hipótesis es minimizar la combinación ponderada de estos errores, expresada como:

\[w_1\cdot\text{Error de Tipo I } + w_2\cdot\text{Error de Tipo II};\]

donde $w_1,w_2$ son constantes. Sin embargo, esta estrategia puede producir una asimetría entre las hipótesis, ya que puede ser difícil o costoso cumplir con ambas condiciones al mismo tiempo. En general, se da mayor énfasis al control del Error de Tipo I, es decir, a la condición en la Ecuación 10.1.

Definición 10.4 Una prueba que satisface la Ecuación 10.1 se denomina prueba de nivel o significancia $\alpha$ y decimos que la prueba está a un nivel de significancia $\alpha$. El tamaño $\alpha(\delta)$ de una prueba $\delta$ se define como:

\[\alpha(\delta) = \sup_{\theta\in\Omega}\pi(\theta|\delta).\]

Corolario 10.1 Una prueba $\delta$ es una prueba de nivel $\alpha$ si y solo si su tamaño es a lo sumo $\alpha$ ($\alpha(\delta)\leq\alpha$).

Ejemplo 10.6 Supongamos que tenemos una muestra $X_1,\dots,X_n$ proveniente de una distribución Uniforme(0, $\theta$), donde $\theta>0$ es desconocido. Queremos probar las siguientes hipótesis:

\[H_0: 3\leq\theta\leq 4 \quad H_1:\theta<3 \text{ o }\theta>4. \]

El estimador de máxima verosimilitud (MLE) de $\theta$ es $Y_n = X_{(n)}$. Si $n$ es grande, $Y_n$ es muy cercano a $\theta$.

Definimos una prueba $\delta$ que no rechaza $H_0$ si $2.9<Y_n<4$ y rechaza $H_0$ si $Y_n\geq4$ o $Y_n\leq2.9$. Por lo tanto, $R = (-\infty, 2.9] \cup [4,+\infty)$ y la función de potencia es \[\pi(\theta|\delta) = \mathbb P[Y_n\leq 2.9|\theta]+\mathbb P[Y_n\geq4|\theta] \]

Calculamos $\pi(\theta|\delta)$ en varios casos:

Si $\theta\leq 2.9$: $\mathbb P[Y_n\leq 2.9|\theta] = 1$ y $\mathbb P[Y_n\geq4|\theta] = 0$.
Si $2.9<\theta\leq4$: $\mathbb P[Y_n\leq 2.9|\theta] = 1 - \prod_{i=1}^n \mathbb P[X_i\leq2.9|\theta] = \left(\dfrac{2.9}{\theta}\right)^n$ y $\mathbb P[Y_n\geq4|\theta] = 0$.
Si $\theta>4$: $\mathbb P[Y_n\leq 2.9|\theta] = \left(\dfrac{2.9}{\theta}\right)^n$ y $\mathbb P[Y_n\geq 4|\theta] = 1 - \displaystyle\prod_{i=1}^n \mathbb P[X_i<4|\theta] = 1-\left(\dfrac 4\theta\right)^n$.

Finalmente, obtenemos

\[\pi(\theta|\delta) = \begin{cases}1 & \text{si } \theta\leq 2.9 \\\left(\dfrac{2.9}{\theta}\right)^n& \text{si } 2.9 <\theta\leq 4\\1+\left(\dfrac{2.9}\theta\right)^n-\left(\dfrac{4}\theta\right)^n & \text{si } \theta >4\end{cases}\]

theta <- seq(1, 5, length.out = 1000)
n <- 5

funcion_poder <- numeric()

for (k in 1:length(theta)) {
  if (theta[k] < 2.9) {
    funcion_poder[k] <- 0
  } else if (theta[k] > 2.9 & theta[k] <= 4) {
    funcion_poder[k] <- (2.9 / theta[k])^n
  } else if (theta[k] > 4) {
    funcion_poder[k] <- (2.9 / theta[k])^n + 1 - (4 / theta[k])^n
  }
}

plot(theta, funcion_poder, type = "l")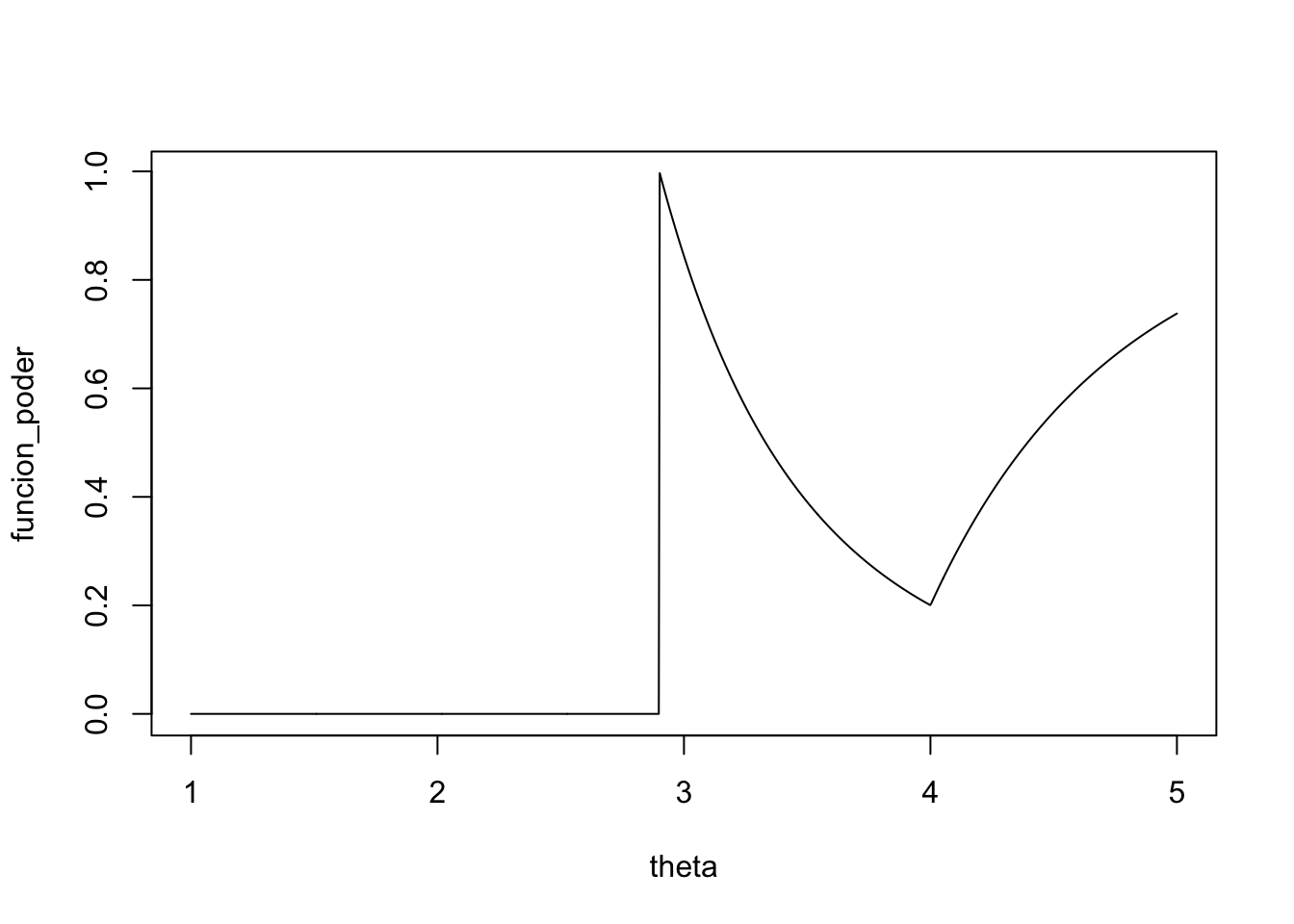

Note, además, que el tamaño de prueba es

\[\alpha(\delta) = \sup_{3\leq\theta\leq 4} \pi(\theta|\delta) = \sup_{3\leq\theta\leq 4}\left(\dfrac{2.9}{\theta}\right)^n = \left(\dfrac{2.9}{3}\right)^n.\]

n <- 1:100
plot(n, (2.9 / 3)^n)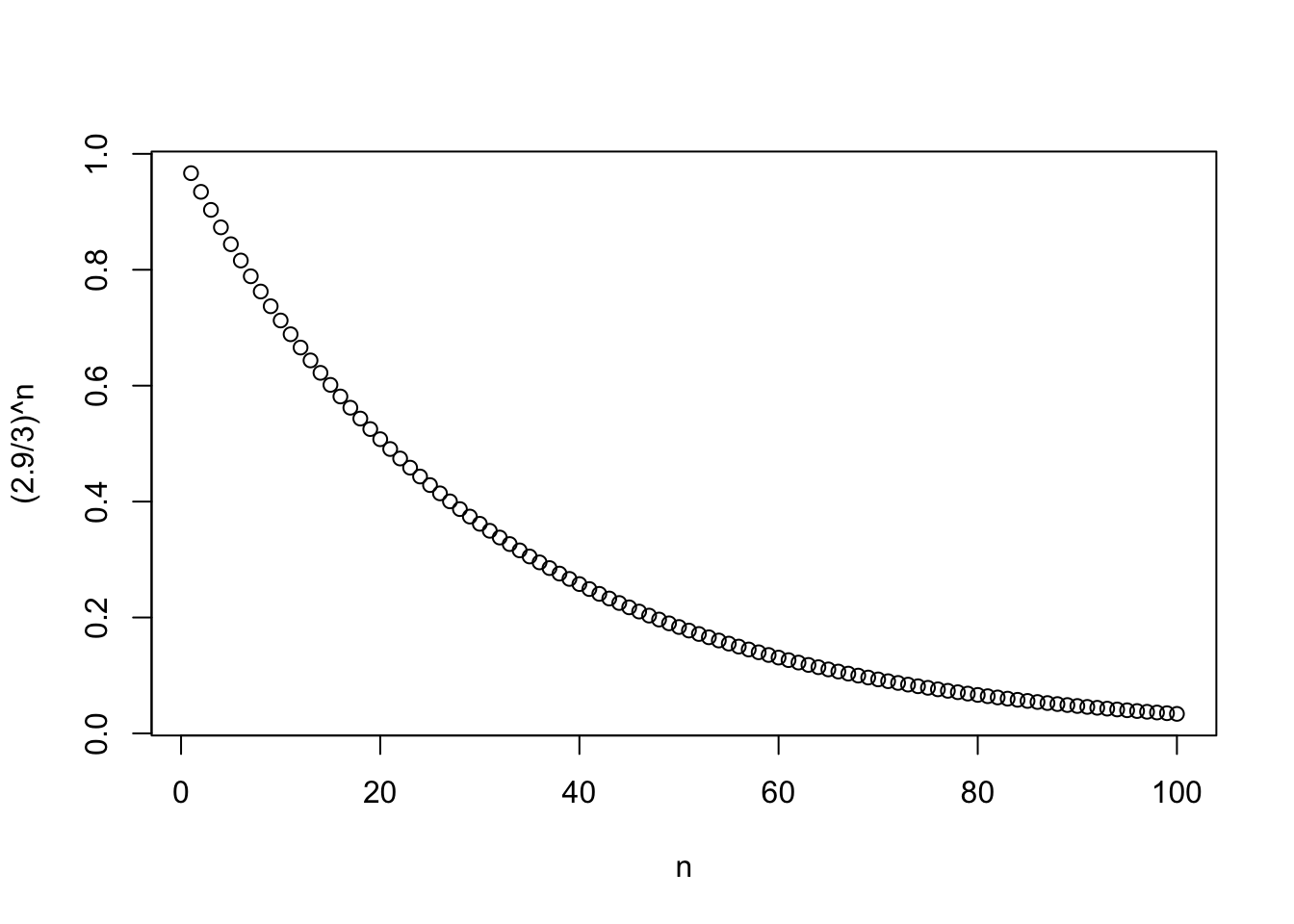

Si $n=100$ entonces $\alpha(\delta) = \left(\dfrac{2.9}{3}\right)^{100}=0.0337$. Esto significa que $\delta$ es una prueba de nivel de significacia $\alpha\geq 0.0337$.

Por otro lado, si $n=10$ entonces $\alpha(\delta) = \left(\dfrac{2.9}{3}\right)^{10} = 0.376$.

Una pregunta importante que surge al trabajar con pruebas de hipótesis es: ¿Cómo podemos diseñar una prueba para que tenga un cierto nivel de significancia?

Supongamos que queremos probar $H_0: \theta \in \Omega_0$ frente a $H_1: \theta\in\Omega_1$. Sea $T$ un estadístico de prueba y suponga que si $T\geq c$, $c$ constante, entonces rechazamos $H_0$.

Si queremos que nuestra prueba tenga un nivel de significancia $\alpha$, entonces:

\[\pi(\theta|\delta) = \mathbb P(T\geq c|\theta)\text{ y } \sup_{\theta \in \Omega_0}\mathbb P[T\geq c|\theta] \leq \alpha \tag{10.2}\]

Note que $\pi(\theta|\delta)$ es una función no creciente de $c$, entonces las condiciones en 10.2 se cumple para valores grandes de $c$, si $\theta\in\Omega_0$. Si $\theta \in \Omega_1$, debemos escoger $c$ pequeño para maximizar $\pi(\theta|\delta)$.

Ejemplo 10.7 Consideremos el caso normal, donde $H_0: \mu = \mu_0$ y rechazamos $H_0$ si $|\bar X_n-\mu_0|\geq c$. En este caso:

\[\sup_{\theta\in\Omega_0} \mathbb P [T\geq c\mid\theta] = \mathbb P_{\mu_0}[\vert\bar X_n-\mu_0\vert\geq c]\geq \alpha.\]

Dado que bajo $H_0$: $Y = X_n-\mu_0 \sim N\left(0,\dfrac{\sigma^2}{n}\right)$, podemos encontrar $c$ tal que \[\mathbb P[|\bar X_n-\mu_0|\geq c] = \alpha,\] y cualquier $c$ mayor va a cumplir Ecuación 10.2.

De esta manera, el problema se convierte en encontrar $c^{\star}$ tal que $\mathbb P[\left| Z \right| >c^{\star}]s = \alpha$, donde $Z = \dfrac{\bar X_n - \mu_0}{\sigma/\sqrt n}$.

Podemos expresar $\alpha$ de la siguiente manera:

\[\begin{align*} \alpha &= \mathbb{P}(|Z|>c^{\star}) \\ &= \mathbb{P}(Z >c^{\star}) + \mathbb{P}(Z < -c^{\star}) \\ &= 1- \mathbb{P}(Z \leq c^{\star}) + \mathbb{P}(Z < -c^{\star}) \\ &= 1- \mathbb{P}(Z \leq c^{\star}) + 1 - \mathbb{P}(Z < c^{\star}) \\ &= 2 - 2 \mathbb{P}(Z \leq c^{\star}) \end{align*}\]

Entonces

\[\begin{equation*} \mathbb{P}(Z \leq c^{\star}) = 1- \dfrac{\alpha}{2} \end{equation*}\]

Por lo tanto el $c^{\star}$ que se busca es

\[\begin{equation*} c^{\star} = F^{-1}\left(1- \dfrac{\alpha}{2}\right) \end{equation*}\]

En el caso particular de la normal denotaremos $F$ como $\Phi$. Entonces,

\[\Phi(c^{\star}) = 1 - \dfrac{\alpha}2 \implies c^{\star} = z_{1-\frac{\alpha}2}.\]

Procedimiento: rechazamos $H_0$ si \[|Z| = \bigg| \dfrac{\bar X_n-\mu_0}{\sigma/\sqrt n}\bigg| \geq z_{1-\frac{\alpha}2}.\]

# Ejemplo con un tamaño de muestra de 10
# y nivel de significancia de 0.05
n <- 10
alpha <- 0.05
x <- rnorm(n = n, mean = 5, sd = 1)
x_bar <- mean(x)
mu_0 <- 5

z <- sqrt(n) * (x_bar - mu_0) / 1

(q <- qnorm(1 - alpha / 2))

[1] 1.959964

dnorm_limit <- function(x, q) {
  y <- dnorm(x)
  y[-q <= x & x <= q] <- NA
  return(y)
}

ggplot(data.frame(x = c(-3, 3)), aes(x)) +
  stat_function(
    fun = dnorm_limit, geom = "area", args = list(q = q),
    fill = "blue", alpha = 0.2
  ) +
  stat_function(fun = dnorm) +
  cowplot::theme_cowplot()

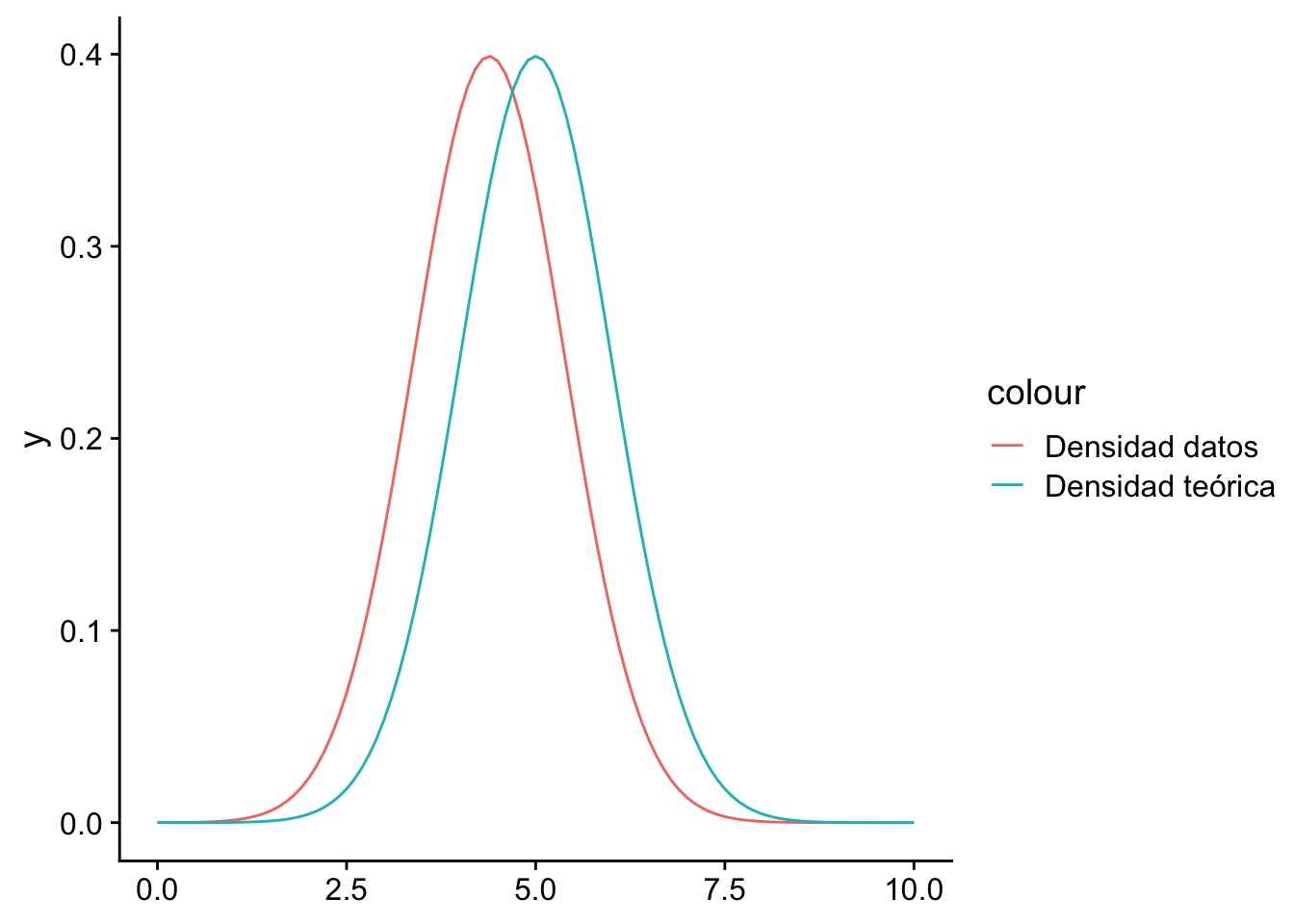
La pregunta que debemos siempre responder es ¿Rechazamos $H_0$?

abs(z) > q

[1] FALSE

Si repetimos el ejercicio anterior, pero los datos tiene media igual a 1 y dejamos que $\mu_0 = 5$, entonces

n <- 10
alpha <- 0.05
x <- rnorm(n = n, mean = 1, sd = 1)
x_bar <- mean(x)
mu_0 <- 5

z <- sqrt(n) * (x_bar - mu_0) / 1

Si preguntamos ¿Rechazamos $H_0$?

abs(z) > q

[1] TRUE

mu_0 <- 5
n <- 10
sigma <- 1
alpha <- 0.05
c <- qnorm(1 - alpha / 2) * sigma / sqrt(n)

mu <- seq(3, 7, length.out = 1000)

funcion_de_poder <- 1 -
    pnorm(sqrt(n) * (mu_0 + c - mu) / sigma) +
    pnorm(sqrt(n) * (mu_0 - c - mu) / sigma)

plot(mu, funcion_de_poder, type = "l", lwd = 2)
abline(h = 0.05, col = "red", lwd = 2)

Ejemplo 10.8 Consideremos un experimento donde se realizan $n$ ensayos Bernoulli independientes, cada uno con probabilidad de éxito $p$. Supongamos que queremos contrastar las hipótesis. $H_0: p\leq p_{0} \text{ vs } H_1: p>p_0$

Sea $Y = \sum_{i=1}^nX_i \sim \text{Binomial}(n,p)$. La idea acá es que entre más grande es $p$ entonces $Y$ será más grande. Podemos definir la regla de que rechazamos $H_0$ si $Y\geq c$ para alguna constante $c$.

El error tipo I es

\[\mathbb P[Y\geq c\mid p] = \sum_{y=c}^n{n\choose y}p^y(1-p)^{n-y} = \sum_{y=c}^n{n\choose y} \underbrace{\left(\dfrac p{1-p}\right)^y(1-p)^n}_{g(p)}\]

Aquí, $g(p)$ es monótona con respecto a $p$, por lo que \[\sup_{p\leq p_0} \mathbb P[Y\geq c\mid p] = \mathbb P [Y\geq c\mid p_0] \leq \alpha.\]

Si $n=10$, $p_0 = 0.3$, $\alpha = 10\%$, entonces

c	0	1	2	3	4	5
$\mathbb P[Y\geq \mid p_0]$	1	0.97	0.85	0.62	0.15	0.05

Para que el tamaño sea menor que $10\%$ seleccione $c>5$. Si $c\in [5,6]$ entonces el nivel de significancia es a lo sumo $0.15$ y la prueba no cambia (ya que $Y$ es una variable discreta).

c <- 5
n <- 10
alpha <- 0.05
p <- seq(0, 1, length.out = 1000)

funcion_de_poder <- 1 - pbinom(q = c, size = n, prob = p)

plot(p, funcion_de_poder, type = "l", lwd = 2)
abline(h = 0.05, col = "red", lwd = 2)

Procedimiento: rechazamos $H_0: p \leq 0.3$ si $Y\geq c$, $c\in(5,6]$ con un nivel de significancia de $10\%$ a lo sumo.

10.3 Valor $p$

Una restricción de los procedimientos de prueba es que dependen de $\alpha$. Es decir, no tenemos una certeza cuál valor de $\alpha$ es el correcto. Por ejemplo, si $\alpha = 0.05$ y rechazamos $H_0$ entonces no sabemos si $\alpha = 0.01$ o $\alpha = 0.001$ es el correcto.

Para esto nos preguntamos, ¿será posible construir un estadístico que resuma el grado de evidencia en los datos en contra de $H_0$?

Usaremos dos fuentes de información:

El valor observado del estadístico de prueba.
Todos los valores de $\alpha$ en donde rechazamos la hipótesis nula.

Ejemplo 10.9 En una prueba de hipótesis en la que se está probando $H_0: \mu = \mu_0$ contra una hipótesis alternativa, rechazamos la hipótesis nula si $|Z| > z_{1-\frac{\alpha}{2}}$. Suponga que observamos los siguientes valores de $Z$: $Z = 1.97, 2.78, 6.97$. Todos estos cumplen la condición de rechazo para $\alpha = 0.05$ y $z_{1-\frac{\alpha}{2}} = 1.96$.

Para comparar la “fuerza” de estos valores de $Z$, podemos calcular el valor $p$ asociado, que es el nivel más pequeño de significancia en donde rechazaríamos $H_0$ bajo los datos observados. Para calcular el valor $p$ asociado con cada valor de $Z$, utilizamos la función de distribución acumulativa de la distribución normal estándar, $\Phi$:

\[\begin{align*} \Phi(Z) &> 1-\dfrac{\alpha}2 \\ \alpha &> 2(1-\Phi(Z)) \end{align*}\]

Si $Z=1.97$ entonces $\alpha =0.0488384$
Si $Z=2.78$ entonces $\alpha =0.0054359$
Si $Z=6.97$ entonces $\alpha =3.1694647\times 10^{-12}$

En cada caso se estimó usando el comando 2*(1-pnorm(1.97)). Como dijimos anteriormente, el valor $\alpha$ es el nivel de significancia.

Definición 10.5 El valor-$p$ es el nivel más pequeño de significancia en donde rechazaríamos $H_0$ bajo los datos observados.

Tip

El valor $p$ resume la evidencia en los datos en contra de la hipótesis nula $H_0$. El valor $p$ se basa en el valor observado del estadístico de prueba y todos los valores de $\alpha$ en los que rechazamos la hipótesis nula.

Además, el valor-$p$ es un estadístico y se puede tomar reglas muy sencillas de decisión:

Si el valor-p es más pequeño que $\alpha$, lo que dice es que si asumes que $H_0$ es verdadera, estás obteniendo resultados poco probables de que ocurran. En este caso, deberías dudar de que $H_0$ es verdadera.
Si el valor-p es más grande que $\alpha$, lo que dice es que si asumes que $H_0$ es verdadera, estas obteniendo resultados muy probables que ocurran de acuerdo a ese nivel. En este caso, deberías creer que $H_0$ es verdadera.

10.3.1 Cálculo del valor-$p$

Para calcular el valor $p$ cuando la región de rechazo es $T \geq c$, utilizamos la función de distribución acumulativa $F$ de $T$. En este caso, el valor $p$ es el nivel más pequeño de significancia en donde $F(t) \geq 1-\alpha$, asumiendo que $H_0$ es verdadero.

\[\begin{align*} & F(t) \geq 1-\alpha \\ \implies & \alpha \geq \mathbb P_\theta[T\geq t]\\ \implies &\alpha \geq \sup_{\theta\in\Omega}P_{\theta}[T\geq t] \end{align*}\]

El tamaño de la prueba es $c=t$.

Ejemplo 10.10 Retomando el ejemplo con las variables aleatorias Bernoulli, rechazamos $H_0: p\leq p_0$ si $Y\geq c$. Así,

\[\text{valor-$p$} = \sup_{p\in\Omega}P_{p}[Y\geq y] =P_{p}[Y\geq y] \]

Si $p_0 = 0.3, n=10, y =6$, entonces el valor correspondiente es $P_{p}[Y\geq 6] = 0.047349$. El código R es pbinom(q = 5, size = 10, prob = 0.3, lower.tail = FALSE)

10.4 Dualidad entre pruebas de hipótesis y regiones de confianza

Teorema 10.1 Sea $x = (X_1,\dots,X_n)$ una muestra con distribución $F_\theta$. Sea $g(\theta)$ una función tal que para cada valor $g_0$ de $g(\theta)$, existe una prueba con nivel $\alpha$ de las hipótesis:

\[H_{0,g_0}: g(\theta) = g_0 \text{ vs } H_{1,g_0}: g(\theta) \neq g_0. \]

Defina para cada $x\in X$

\[\omega(x) = \{g_0: \delta_{g_0} \text{ no rechaza }H_{0,g_0}\text{ si }X=x\} \tag{10.3}\]

Entonces \[\mathbb P[g(\theta_0)\in \omega(x)|\theta = \theta_0 ] \geq 1-\alpha, \;\forall \theta_0 \in \Omega.\]

Teorema 10.2 Si $\omega(x)$ satisface Ecuación 10.3 $\forall \theta_0 \in \Omega$, entonces $\omega(x)$ es un conjunto de confianza con significacia $1-\alpha$.

Teorema 10.3 Bajo las condiciones anteriores, si $\omega(x)$ es un conjunto de confianza para $g_0$, entonces construimos $\delta_{g_0}$: no rechazo $H_{0,g_0}$ si y solo si $g_0 \in \omega(X)$, entonces $\delta_{g_0}$ es una prueba con nivel $$ para $H_{0,g_0}$.

Ejemplo 10.11 Sea $X_1,\dots,X_n\sim N(\mu,\sigma^2)$, $\theta = (\mu,\sigma^2)$ (desconocidos). En este caso $g(\theta) = \mu$. El intervalo de confianza con nivel $1-\alpha$ es

\[\bar X_n\pm t_{n-1,\frac{1-\frac{\alpha}{2}}\dfrac{s_{n}}{\sqrt n}.\]

La hipótesis de interés corresponde a

\[ H_0: \mu = \mu_0 \text{ vs } H_1: \mu \ne \mu_0.\]

Por los teoremas anteriores, $H_0$ se rechaza si $\mu_0$ no está en el IC, es decir, si y solo si

\[\mu_0 > \bar X_n+ t_{n-1,1-\frac{\alpha}{2}}\dfrac{s_{n}}{\sqrt n} \text{ o } \mu_0 < \bar X_n- t_{n-1,1-\frac{\alpha}{2}}\dfrac{s_{n}}{\sqrt n},\]

que se puede resumir como

\[\bigg|\dfrac{\bar X_n-\mu_0}{s_{n}/\sqrt n}\bigg|>t_{n-1,1-\frac{\alpha}2}.\]

n <- 1000
alpha <- 0.05
x <- rnorm(n = n, mean = 1, sd = 2)
mu_0 <- 1

x_bar <- mean(x)
s <- sd(x)

t_quantil <- qt(p = 1 - alpha / 2, df = n - 1)

El intervalo de confianza es

c(
  x_bar - t_quantil * s / sqrt(n),
  x_bar + t_quantil * s / sqrt(n)
)

[1] 1.006977 1.247349

\[ H_0: \mu = 1 \text{ vs } H_1: \mu \ne 1.\]

Para probar esta prueba se debe comprobar que

z <- abs((x_bar - mu_0) / (s / sqrt(n)))

Preguntamos ¿Rechazamos $H_0$?

z > t_quantil

[1] TRUE

Si tuvieramos otros datos con otra media, el resultado será diferente.

n <- 1000
alpha <- 0.05
x <- rnorm(n = n, mean = 5, sd = 2)
mu_0 <- 1

x_bar <- mean(x)
s <- sd(x)

t_quantil <- qt(p = 1 - alpha / 2, df = n - 1)

c(
  x_bar - t_quantil * s / sqrt(n),
  x_bar + t_quantil * s / sqrt(n)
)

[1] 4.939501 5.202789

¿Rechazamos $H_0$?

z <- abs((x_bar - mu_0) / (s / sqrt(n)))
z > t_quantil

[1] TRUE

Ejemplo 10.12 Para una muestra $X_1,\dots,X_n\sim N(\mu,\sigma^2)$, con $\mu$ desconocido y $\sigma^2$ conocido. Construya un intervalo de confianza con nivel $1-\alpha$ a partir de \[ H_0: \mu = \mu_0 \text{ vs } H_1: \mu \ne \mu_0.\]

Rechazamos $H_0$ si \[\bigg|\dfrac{\bar X_n-\mu_0}{\sigma/\sqrt n}\bigg|\geq z_{1-\frac{\alpha}2}.\]

al nivel $\alpha$. Usando los teoremas anteriores, una región de confianza con nivel $1-\alpha$ satisface:

\[\mu\in\bigg\{ \bigg|\dfrac{\bar X_n-\mu}{\sigma/\sqrt n}\bigg|< z_{1-\frac{\alpha}2}\bigg\} = \omega(x)\]

Por tanto,

\[\begin{align*} \bigg|\dfrac{\bar X_n-\mu}{\sigma/\sqrt n}\bigg| & \Leftrightarrow -\dfrac{\sigma}{\sqrt n}z_{1-\frac{\alpha}2}<\bar X_n - \mu<\dfrac{\sigma}{\sqrt n}z_{1-\frac{\alpha}2}\\ & = \Leftrightarrow \bar X_n-\dfrac{\sigma}{\sqrt n}z_{1-\frac{\alpha}2}< \mu<\bar X_n + \dfrac{\sigma}{\sqrt n}z_{1-\frac{\alpha}2} \end{align*}\] que es el IC con nivel $1-\alpha$ para $\mu$.

10.4.1 Dualidad en pruebas unilaterales

Si $x = (X_1,\dots, X_n)$ es una muestra según $F_\theta$ y $g(\theta)$ es una función de variable real, suponga que para cada $g_0\in Im(g)$ existe una prueba $\delta_{g_0}$ con nivel $\alpha$ de las hipótesis anteriores. Si \[\omega(x) = \{g_0: \delta_{g_0} \text{ no rechaza }H_{0,g_0}\text{ si }X=x\}\]

entonces $\omega(x)$ es una región de confianza para $g(\theta)$ con nivel $1-\alpha$.

Ejemplo 10.13 Supongamos que se tiene una muestra de datos Bernoulli y la siguientes hipótesis:

\[ H_0: p \leq p_0 \text{ vs } H_1: p>p_0.\]

El criterio de rechazo al nivel $\alpha$ es

\[Y = \sum_{i=1}^nX_i\geq c(p_0)\]

donde

\[\sup_{p\leq p_0} \mathbb P_p[Y\geq c] = \mathbb P_{p_0}[Y\geq c] \leq \alpha.\]

Entonces

\[\omega(x) = \{p_0: Y<c(p_0)\} = \{p_0: \text{valor-}p>\alpha\}.\]

Si $n=10$, $Y=6$, $\alpha = 10\%$, \[\omega(x) =\{p_0: P_{p_0}[Y> 6] >0.1\}.\]

Numéricamente, si $p_0 > 35.42\% \implies p_0 \in \omega(x)$, entonces $\omega(x) = (0.3542,1]$ si $\alpha=10\%$ y es un IC para $p_0$ con nivel de 90%.

# Parámetros
n <- 10
Y <- 6
alpha <- 0.1

# Función para calcular la región de confianza
omega <- function(p0) {
  pbinom(Y - 1, n, p0, lower.tail = FALSE) > alpha
}

# Encontrar el valor mínimo de p0
(p0_min <- uniroot(function(p) omega(p) - 0.5, c(0, 1))$root)

[1] 0.354126

# Resultado
(omega_x <- c(p0_min, 1))

[1] 0.354126 1.000000

Ejemplo 10.14 $x = (X_1,\dots, X_n)\sim N(\mu,\sigma^2)$, $\theta = (\mu,\sigma^2)$ desconocido. Queremos probar \[ H_0: \mu \leq \mu_0 \text{ vs } H_1: \mu > \mu_0.\] Por dualidad, basta con conocer un IC unilateral para $\mu$:

\[ \left(\bar X_n-t_{n-1,1-\alpha}\dfrac{s_{n}}{\sqrt n},\infty\right).\]

Rechazamos $H_0$ si

\[\mu_0\leq \bar X_n-t_{n-1,1-\alpha}\dfrac{s_{n}}{\sqrt n} \Leftrightarrow T = \dfrac{\bar X_n -\mu_0}{s_{n}/\sqrt n}\geq t_{n-1,1-\alpha}\]

(rechazando en la cola derecha de $T$).

10.5 Pruebas de cociente de verosimilitud (LRT)

Si $H_0:\theta \in \Omega_0$ vs $H_1: \theta \in \Omega_0^c = \Omega_1$. El estadístico LRT se define como

\[\Lambda (x) = \dfrac{\sup_{\theta\in \Omega_0} f_n(x|\theta)}{\sup_{\theta\in \Omega} f_n(x|\theta)}.\]

Una prueba de cociente de verosimilitud rechaza $H_0$ si $\Lambda(x)\leq k$, para una constante $k$.

Ejemplo 10.15 Supongamos que se observa $Y$ el número de éxitos en el experimento $\text{Bernoulli}(\theta)$ con tamaño de muestra $n$.

\[H_0: \theta = \theta_0 \text{ vs } H_1: \theta\ne\theta_0.\]

Verosimilitud: $f(y|\theta) = {n\choose y}\theta ^y(1-\theta)^{n-y}$.
$\Omega_0 = \{\theta_0\}$, $\Omega_1 = [0,1]\setminus \{\theta_0\}$.
Numerador: $f(y|\theta_0)$.
Denominador: $f(y|\bar y) = \displaystyle{n\choose y}{\bar y}^{y}(1-\bar y)^{n-y}$.

\[\Lambda(y) = \dfrac{f(y|\theta_0)}{f(y|\bar y)} = \left(\dfrac{n\theta_0}{y}\right)^y\left(\dfrac{n(1-\theta_0)}{n-y}\right)^{n-y}, \quad y=0,\dots,n.\]

Si $n=10$, $\theta_0 = 0.3$, $y = 6$, $\alpha=0.05$.

n <- 10
p0 <- 0.3
y <- 0:10
alpha <- 0.05

p <- choose(n, y) * p0^y * (1 - p0)^(n - y)

Lambda <- numeric(n)
Lambda[y == 0] <- (1 - p0)^n
ym1 <- y[y != 0]
Lambda[y != 0] <- (n * p0 / ym1)^ym1 *
  ((n * (1 - p0)) / (n - ym1))^(n - ym1)

plot(y, Lambda, type = "l", col = "blue")
lines(y, p, type = "l", col = "red")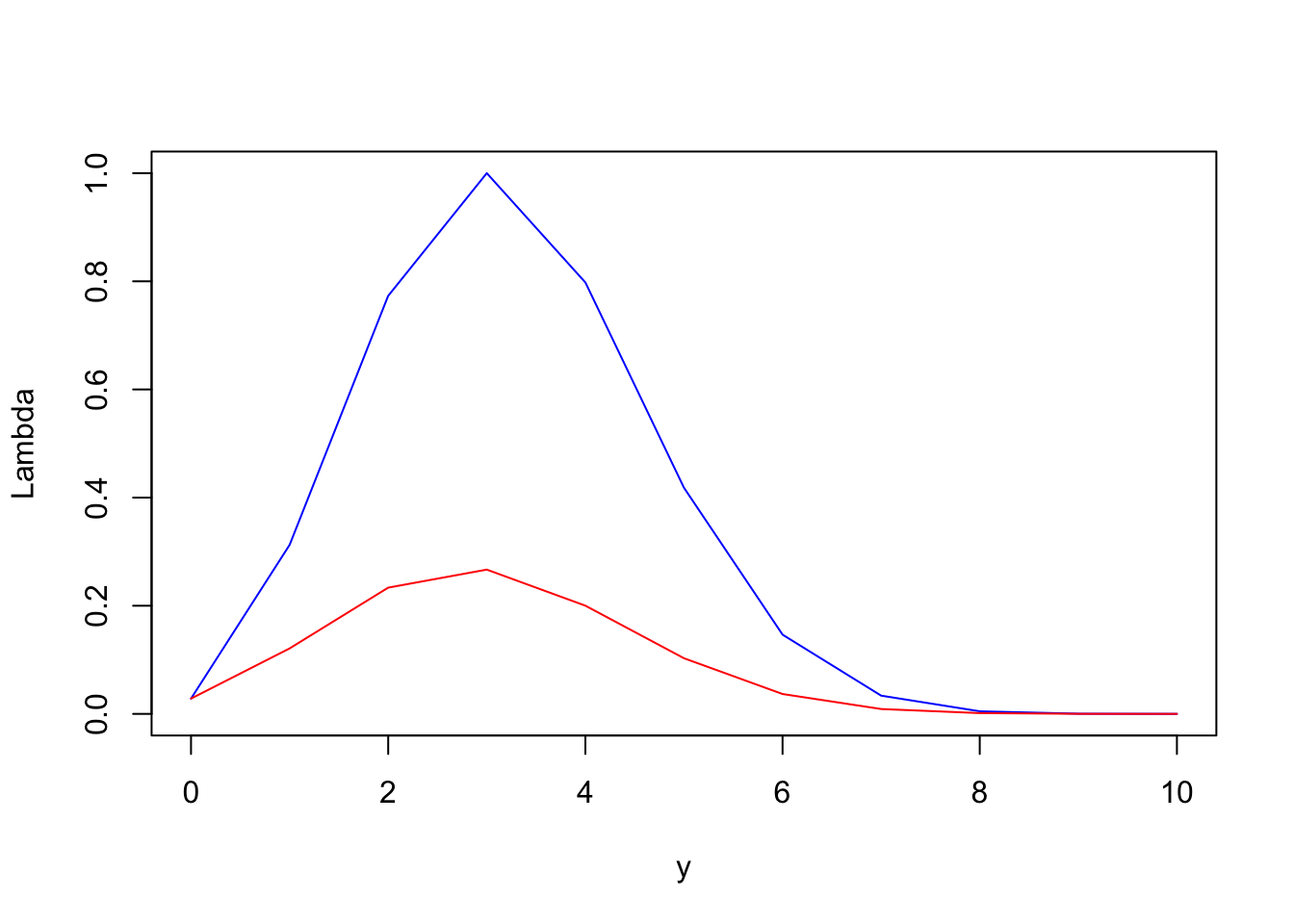

knitr::kable(cbind(y, Lambda, p))

y	Lambda	p
0	0.0282475	0.0282475
1	0.3124791	0.1210608
2	0.7731201	0.2334744
3	1.0000000	0.2668279
4	0.7978583	0.2001209
5	0.4182119	0.1029193
6	0.1465454	0.0367569
7	0.0337359	0.0090017
8	0.0047906	0.0014467
9	0.0003556	0.0001378
10	0.0000059	0.0000059

ix <- order(p)
knitr::kable(cbind(y[ix], cumsum(p[ix])))

10	0.0000059
9	0.0001437
8	0.0015904
7	0.0105921
0	0.0388396
6	0.0755965
5	0.1785159
1	0.2995767
4	0.4996976
2	0.7331721
3	1.0000000

Rechazamos $H_0$ con nivel $\alpha = 0.05$ en $y \in\{10,9,8,7,0\}$ y $k\in [0.028,0.147)$ si rechazo cuando $\Lambda(y)\leq k$. El tamaño de prueba es \[\mathbb P_{0.3}[\text{Rechazo}] = \mathbb{P}_{0.3}[Y\in \{10,9,8,7,0\}] = 0.039.\]

Teorema 10.4 Sea $\Omega$ un abierto en $\mathbb R^p$ y suponga que $H_0$ especifica $k$ coordenadas de $\theta$, igualándolas a valores fijos. Asuma que $H_0$ es cierto y que todas las condiciones de regularidad de $\theta$ son ciertas. \[-2\ln\Lambda(x)\xrightarrow[H_0]{d}\chi^2_k.\]

Ejemplo 10.16 Del caso anterior, $k=1$, $\alpha = 5\%$. Rechazamos $H_0$: \[-2\ln \Lambda(y)>\chi^2_{1,1-0.05} = F^{-1}_{\chi^2_1}(0.95) = 3.841.\]

Rechazamos $H_0$ bajo la misma región del ejemplo anterior.

-2 * log(Lambda)

 [1]  7.1334989  2.3264351  0.5146418  0.0000000  0.4516484  1.7435339
 [7]  3.8408399  6.7783829 10.6822162 15.8832009 24.0794561

qchisq(p = 0.95, df = 1)

[1] 3.841459

¿Rechazamos $H_0$?

knitr::kable(data.frame(y,
  test = -2 * log(Lambda) > qchisq(p = 0.95, df = 1)
))

y	test
0	TRUE
1	FALSE
2	FALSE
3	FALSE
4	FALSE
5	FALSE
6	FALSE
7	TRUE
8	TRUE
9	TRUE
10	TRUE

	\(H_0\) es Verdadera	\(H_0\) es Falsa
Probabilidad de rechazar \(H_0\)	\(\alpha\)	\(1 - \beta\)
Probabilidad de aceptar (no rechazar) \(H_0\)	\(1 - \alpha\)	\(\beta\)

10 Pruebas de hipótesis

10.1 Regiones críticas y estadísticas de prueba

10.2 Función de potencia y tipos de error

10.2.1 Errores de Tipo I y Tipo II

10.3 Valor \(p\)

10.3.1 Cálculo del valor-\(p\)

10.4 Dualidad entre pruebas de hipótesis y regiones de confianza

10.4.1 Dualidad en pruebas unilaterales

10.5 Pruebas de cociente de verosimilitud (LRT)