9  Intervalos de confianza

9.1 Intervalos de confianza para la media de una distribución normal

Dado \(\theta\) un parámetro en \(\mathbb{R}\) hemos estudiado procedimientos para encontrar estadísticos \(T\in \mathbb R\) para estimarlo. La limitación que tenemos acá es que no sabemos que tan aleatorio es \(T\). Entonces podemos sustituir este estadístico \(T\) con otros dos estadísticos \(T_1\) y \(T_2\) de modo que sepamos que \[\begin{equation*} T_1 \leq \theta \leq T_2 \end{equation*}\]

En caso que \(\theta \in \mathbb{R} ^{k}\) se puede construir un conjunto de estadísticos \(T_1, \ldots, T_{k^\prime}\) con \(k^\prime = 2k\) tal que

\[\begin{equation*} \theta \in [T_1, T_2] \times \cdots \times [T_{k^\prime-1}, T_{k^\prime}] \end{equation*}\]

9.2 Caso normal.

En el caso normal, \(\bar X_n\) es un estimador puntual de \(\mu\). ¿Será posible encontrar un estimador para un intervalo?

Para efectos didácticos, primero defina \(U = \dfrac{\sqrt{n}(\bar X_n-\mu)}{s} \sim t_{n-1}\). Recuerde que \(s^2\) se define como la varianza muestral, cuya fórmula es \[ s^2 = \dfrac{1}{n-1} \sum_{i=1}^n (X_i - \bar X_n)^2. \]

Ahora para \(c>0\), queremos encontrar la probabilidad que \(U\) esté en el intervalo \((-c,c)\). Para esto, usaremos la distribución de \(U\):

\[\begin{align*} \mathbb P[-c<U<c] & = \mathbb P \bigg[ -c<\dfrac{\sqrt{n}(\bar X_n-\mu)}{s} <c\bigg] \\ & = \mathbb P \bigg[-\dfrac{cs}{\sqrt n} < \bar X_n - \mu <\dfrac{cs}{\sqrt n}\bigg] \\ & = \mathbb P \bigg[ \bar X_n -\dfrac{cs}{\sqrt n} < \mu < \bar X_n + \dfrac{cs}{\sqrt n}\bigg] \end{align*}\]

El intervalo

\[\begin{equation*} T = \bigg[\bar X_n - \dfrac{c s}{\sqrt n},\bar X_n + \dfrac{c s}{\sqrt n}\bigg] \end{equation*}\]

es un intervalo aleatorio que “contiene” a \(\mu\). Tome \(\alpha \in (0,1)\) de modo que: \[ \mathbb P(\mu\in T) = 1-\alpha. \]

Para que se cumpla lo anterior, seleccione \(c\) tal que

\[\begin{align*} 1-\alpha = \mathbb P( \mu \in T) & = \mathbb{P}_{t_{n-1}}(U \leq c)- \mathbb{P}_{t_{n-1}}(U \leq -c) \\ & = F_{t_{n-1}}(c)-F_{t_{n-1}}(-c) \\ & = F_{t_{n-1}}(c) - [1-F_{t_{n-1}}(c)] \\ & = 2F_{t_{n-1}}(c) - 1 \end{align*}\]

Entonces despejando se obtiene que

\[\begin{align*} 1-\frac{\alpha}{2} & = F_{t_{n-1}}(c) \\ \implies c & = F_{t_{n-1}}^{-1}\left(1-\frac{\alpha}{2}\right). \end{align*}\]

Definición 9.1 Si \(X\) es una variable aleatoria continua con distribución \(F\) (monótona creciente), entonces \(x=F^{-1}(p)\) es el cuantil de orden \(p\) de \(F\) (\(p\)-cuantil).

El intervalo de confianza,

\[\begin{equation*} \bigg[\bar X_n - F_{t_{n-1}}^{-1}\left(1-\frac{\alpha}{2} \right)\dfrac{ s}{\sqrt n},\bar X_n + F_{t_{n-1}}^{-1}\left(1-\frac{\alpha}{2} \right)\dfrac{ s}{\sqrt n}\bigg] \end{equation*}\]

contiene a \(\mu\) con probabilidad \(1-\alpha\).

Definición 9.2 Sea \(X = (X_1,\dots,X_n)\) una muestra con parámetro \(\theta\). Sea \(g(\theta)\) una característica de la distribución que genera la muestra. Sea \(A < B\) dos estadísticos que cumplen (\(\forall \theta\)): \[ \mathbb P [A<g(\theta)<B]\geq 1-\alpha. \tag{9.1}\]

Al intervalo \((A,B)\) le llamamos intervalo de confianza al \(100 (1-\alpha)\%\). En el caso que Ecuación 9.1 tenga una igualdad, el intervalo es exacto.

Observación. En algunos textos se usa \(\gamma\) en lugar de \(1-\alpha\), donde \(\gamma\) es cercano a 1. En este caso, se dice que el intervalo es un intervalo de confianza al \(100\gamma \%\), y se escribe como \[\begin{equation*} \bigg[\bar X_n - F_{t_{n-1}}^{-1}\left(\frac{1+\gamma}{2} \right)\dfrac{ s}{\sqrt n},\bar X_n + F_{t_{n-1}}^{-1}\left(\frac{1+\gamma}{2} \right)\dfrac{ s}{\sqrt n}\bigg] \end{equation*}\]

Observación. Si observamos \(X\), calculamos \(A=a\), \(B=b\). Entonces \((a,b)\) es el valor observado de un intervalo de confianza.

Ejemplo 9.1 Se realiza un experimento donde se inyectan nubes con sulfato de plata y de obtiene la cantidad de agua de lluvia. El experimento se hizo con \(n=26\) observaciones. Se desea hacer inferencia sobre \(\mu\), la cantidad de lluvia media (escala logarítmica). Los datos se pueden aproximadamente así

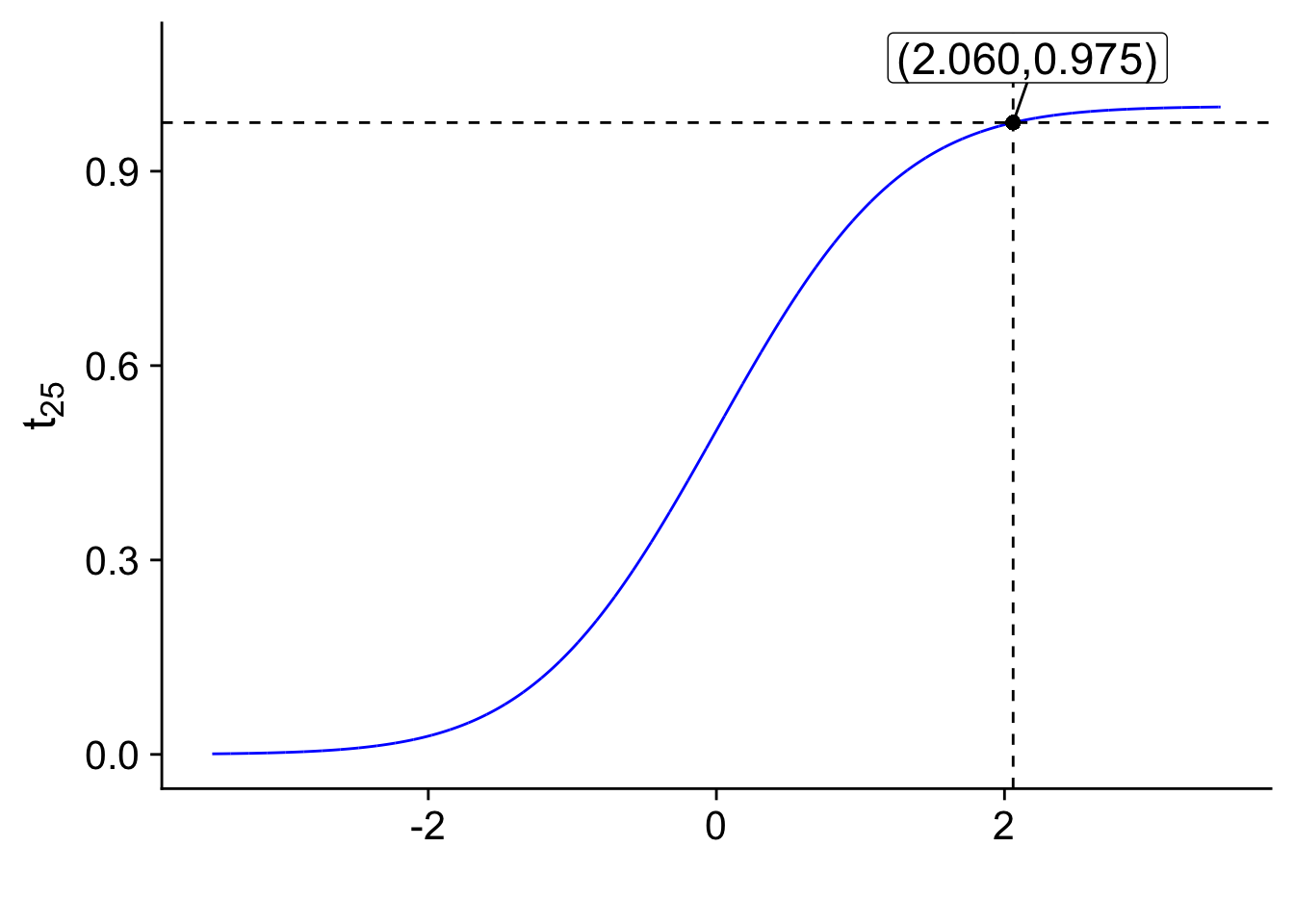
Para \(\alpha=0.05\), se calcula

\[ c=F^{-1}_{t_{25}}\left(1-\frac{\alpha}{2}\right) =F^{-1}_{t_{25}}(0.975) = 2.060 \]

Note que \(1-\frac{\alpha}{2}=\) \(0.975\) y \(n-1 = 26-1=25\). El valor final se obtiene de una tabla de valores de la \(t\)-student o de la expresión qt(p = 0.975, df = 25) = \(2.06\)

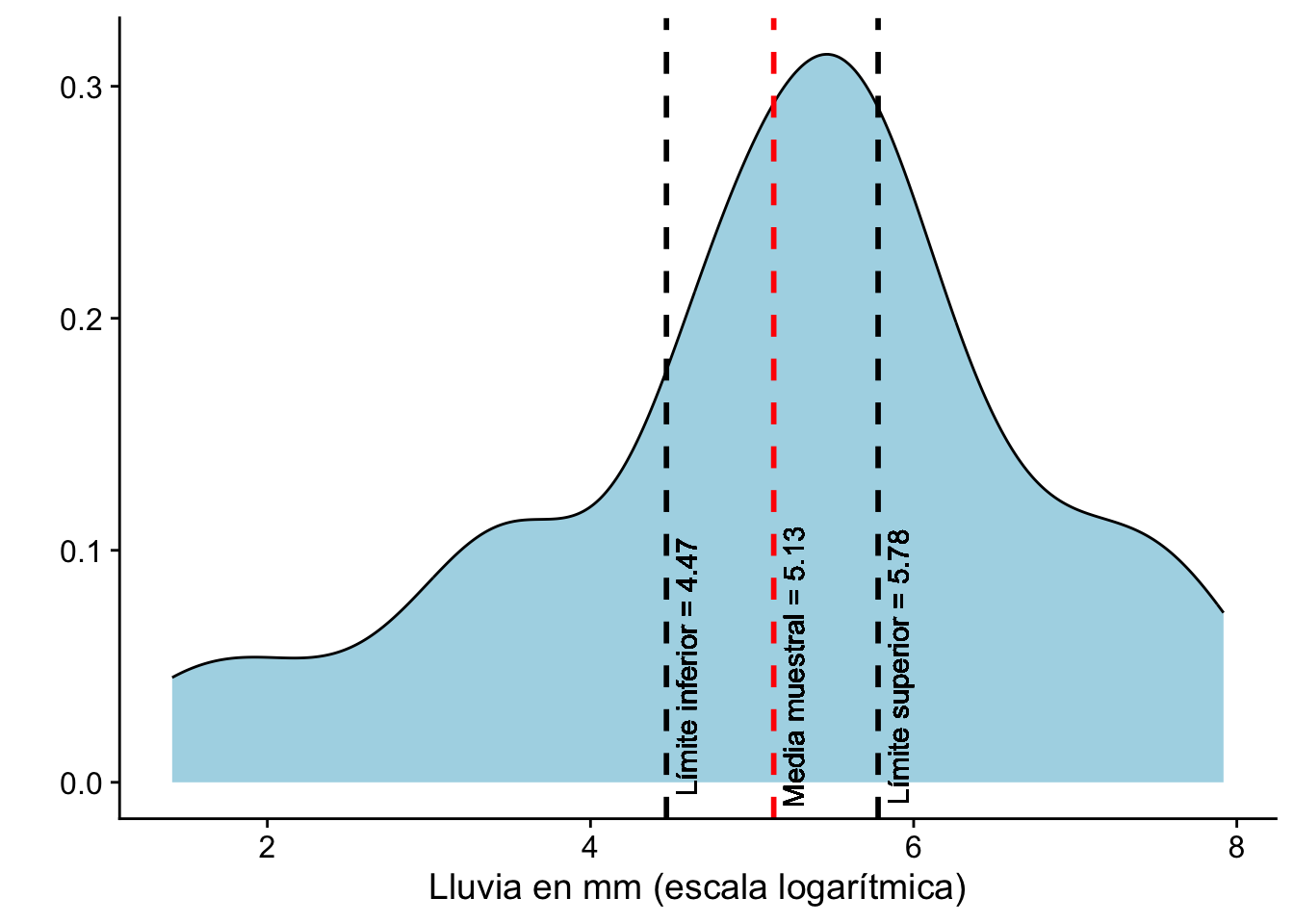
El intervalo de confianza para \(\mu\) al \(95\%\) es

\[\begin{align*} \bar X_n & \pm \frac{c}{\sqrt{n}} s \\ \bar X_n & \pm \frac{2.060}{\sqrt{26}}s \\ \bar X_n & \pm 0.404 s \end{align*}\]

Si \(\bar X_n = 5.134\) y \(s = 1.6\) el valor observado del intervalo de confianza al \(95\%\) para \(\mu\) corresponde a

\[\begin{equation*} [5.134-0.404\cdot1.6, 5.134+0.404\cdot1.6]= [4.47,5.78] \end{equation*}\]

Observación (Interpretación técnica). El intervalo observado \([4.48,5.78]\) contiene a \(\mu\) con un nivel de confianza del \(95%\). Usualmente a \(\dfrac{c s}{\sqrt{n}}\) se le llama margen de error (MOE).

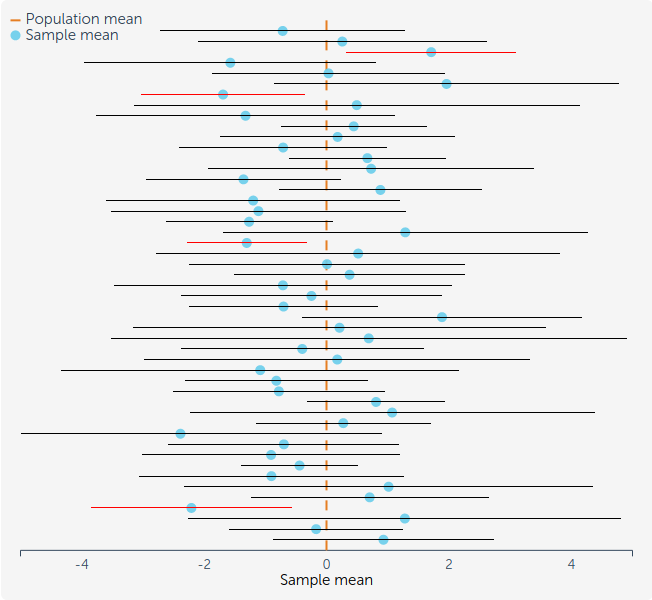
Observación (Interpretación gráfica). El proceso de construir un intervalo de confianza, quiere decir que si usted repitiera ese experimento muchas veces, el \(100(1-\alpha)\%\) (e.g, 95% o 99%) de la veces, el intervalo escogido tendría el parámetro real de la población \(\theta\).

Ejemplo interactivo sobre intervalos de confianza. Tomado de (R Psycologist)[https://rpsychologist.com/d3/ci/]

9.3 Intervalos de Confianza Asimétricos

Los intervalos de confianza no siempre son simétricos en torno a un valor estimado. En ciertos contextos, puede ser útil considerar intervalos de confianza de un solo lado.

Dado un nivel de confianza \(1-\alpha\), supongamos que existen dos valores \(\gamma_1\) y \(\gamma_2\) con \(\gamma_2 -\gamma_1 = 1-\alpha\). Definamos el estadístico \(U\) como:

\[ U = \frac{\sqrt n}{s}(\bar X_n-\mu) \]

Si \(T_{n-1}^{-1}(c)\) representa el cuantil de nivel \(c\) de la distribución del estadístico, los límites del intervalo de confianza pueden ser definidos como:

\[ A = \bar X_n - T_{n-1}^{-1}(\gamma_1)\dfrac{ s}{\sqrt n} \] \[ B = \bar X_n + T_{n-1}^{-1}(\gamma_2)\dfrac{ s}{\sqrt n} \]

El intervalo \((A,B)\) es un intervalo de confianza al \(100(1-\alpha)\%\) ya que:

\[ \mathbb P[\mu \in (A,B)] = \gamma_2-\gamma_1 = (1-\alpha) \]

Definición 9.3 (Intervalos de Confianza Abiertos) En ciertas situaciones, puede ser útil considerar intervalos de confianza que no están acotados en uno de sus extremos.

• Límite Inferior de Confianza: Si \(A\) es un estadístico que cumple: \[ \mathbb P [A<g(\theta)]\geq 1-\alpha \] Entonces, \(A\) es el límite inferior de confianza al \(100(1-\alpha)\%\). El intervalo \((A,\infty)\) es el intervalo de confianza inferior al \(100(1-\alpha)\%\).

• Límite Superior de Confianza: De manera análoga, si \(B\) cumple: \[ \mathbb P [g(\theta)<B]\geq 1-\alpha \] El intervalo \((- \infty,B)\) es el intervalo de confianza superior para \(g(\theta)\) con nivel \(1-\alpha\). Si se cumple la igualdad, el intervalo es exacto.

Ejemplo 9.2 Consideremos una distribución normal. Queremos encontrar un valor \(B\) tal que \(\mathbb P(\mu<B) = 1-\alpha\). Sabemos que:

\[F_{t_{n-1}}(c) = \mathbb P(U>-c) = \mathbb P \left(\dfrac{\sqrt n(\mu - \bar X_n)}{ s}<c\right)\]

De aquí, podemos expresar \(1-\alpha\) como:

\[1-\alpha = \mathbb P\left(\mu < \bar X_n + \dfrac{ s}{\sqrt n}c\right)\]

Para encontrar \(c\), tomamos:

\[F_{t_{n-1}}(-c) = 1-\alpha \implies c = -F_{t_{n-1}}^{-1}(1-\alpha)\]

Finalmente, el límite superior \(B\) del intervalo de confianza es:

\[B = \bar X_n - \dfrac{ s_n}{\sqrt{n}}F^{-1}_{t_{n-1}}(1-\alpha)\]

Ejemplo 9.3 Ahora si retomamos el Ejemplo 9.1, pero ahora queremos el 90% intervalo de confianza para \(\mu\). Entonces \(T_{25}^{-1}(0.9)\) se calcula con el comando qt(p = 0.90, df = 25) = \(1.316\). El intervalo de confianza quedaría

\[\begin{equation*} a = 5.1314 - 1.316 \frac{1.600}{\sqrt{26}} = 4.727. \end{equation*}\]

9.4 Intervalos de confianza en otros casos

Importante

Recuerden lo siguiente: para calcular un intervalo de confianza ustedes solo necesitan saber el estadístico del parámetro \(\theta\) y la distribución de ese estadístico. Con esa distribución calculan el cuantil de tamaño \(1-\alpha\) de modo que la probabilidad de que el parámetro \(\theta\) esté en el intervalo sea \(1-\alpha\).

Ejemplo 9.4 Retomemos el ejemplo de los componentes electrónicos que fallan. Recordemos que el tiempo de vida de estos componentes sigue una distribución exponencial con parámetro \(\theta\). En el experimento, se observaron 3 aparatos, es decir, \(n=3\) y \(X_i \sim \text{Exp}(\theta)\). A partir de nuestros datos, determinamos que si \(T = \sum_{i=1}^3X_i\), entonces \(\theta T \sim \Gamma(3,1)\).

Queremos construir un intervalo de confianza superior para \(\theta\) al \(100(1-\alpha)\%\) (exacto). Esto se traduce en encontrar un valor \(B\) tal que \(\mathbb P[\theta<B] = 1-\alpha\).

Si \(G\) representa la función de distribución acumulada de la distribución gamma, entonces:

\[1-\alpha = \mathbb{P}[\theta T<G^{-1}(1-\alpha)] = \mathbb{P}\left[\theta<\frac{G^{-1}(1-\alpha)}{T}\right]\]

Por lo tanto, el límite superior del intervalo de confianza es:

\[B = \frac{G^{-1}(\gamma)}{T}\]

# Establecemos una semilla para reproducibilidad
set.seed(123)

# Definimos el valor de theta
theta <- 2

# Generamos 3 valores aleatorios de una distribución exponencial
(X <- rexp(3, rate = theta))

[1] 0.4217286 0.2883051 0.6645274

# Calculamos la suma de estos valores
(T <- sum(X))

[1] 1.374561

# Obtenemos el cuantil 0.95 de una distribución gamma con forma 3 y tasa 1
(G_inv <- qgamma(p = 0.95, shape = 3, rate = 1))

[1] 6.295794

# Calculamos el intervalo de confianza
c(0, G_inv / T)

[1] 0.000000 4.580221

El siguiente concepto encierra la esencia de la contrucción de los intervalos de confianza. Básicamente, trataremos de transformar nuestro estimador a una cantidad que no dependa del parámetro \(\theta\) o una cantidad pivotal. Para esto primero debemos definir este término.

Definición 9.4 Dada una muestra \(X = (X_1,\dots,X_n)\) proveniente de una distribución \(F_\theta\), si tenemos una variable aleatoria \(V(X,\theta)\) cuya distribución no depende de \(\theta\), entonces decimos que \(V\) es una cantidad pivotal.

En mucho casos el truco para construir intervalos de confianza, es invertir la cantidad pivotal. La idea es encontrar una función \(r(v,x)\) que satisface:

\[r(V(X,\theta), X) = g(\theta)\]

donde \(g\) es una función arbitraria.

Si esta función existe, entonces es posible encontrar un intervalo de confianza para \(\theta\) al \(100(1-\alpha)\%\) de la siguiente manera:

Intervalos asimétricos

Si la función \(r(v,x)\) es creciente en \(v\) para cada \(x\) y tenemos que \(\gamma_2 > \gamma_1\) con \(\gamma_2-\gamma_1=1-\alpha\), entonces los límites del intervalo de confianza son:

\[\begin{align*} A & = r(G^{-1}(\gamma_1),X) \\ B & = r(G^{-1}(\gamma_2),X) \end{align*}\]

Si \(r(v,x)\) es decreciente, simplemente intercambiamos \(A\) y \(B\).

Ejemplo 9.5 Retomando el ejemplo anterior donde \(V(X,\theta) = \theta T\), podemos elegir:

\[r(v,x) = \frac{v}{t}\]

donde \(t = \sum_{i=1}^{3} X_i\). Así, obtenemos:

\[r(V(X,\theta),X) = \frac{V(X,\theta)}{T} = \theta = g(\theta).\]

Ejemplo 9.6 Suponga que \(X_1,\dots, X_n \stackrel{i.i.d}{\sim} N(\mu,\sigma^2)\). Encuentre A, B tales que \(\mathbb P[A<\sigma^2<B] = 1-\alpha\).

Se sabe que \[\dfrac{n\hat\sigma^2}{\sigma^2}\sim \chi^2_{n-1}.\]

Tome \(V(X,\sigma^2) = \dfrac{n\hat\sigma^2}{\sigma^2}\). Entonces

\[1-\alpha = \mathbb P[\chi^2_{n-1,\gamma_1}<V(X,\sigma^2)<\chi^2_{n-1,\gamma_2}]\]

Ahora, defina la función \[r(v,X) =\frac{\sum_{i=1}^{n}{(X_i -\bar X_n)}^2}{v} = \dfrac{n\hat{\sigma}^2}{v}.\]

Esta función cumple que

\[r(V(X,\sigma^2),X) = \dfrac{n\hat{\sigma}^2}{\dfrac{n\hat{\sigma}^2}{\sigma^2}} = \sigma^2.\]

Entonces las siguientes igualdades son verdaderas

\[\begin{align*} & = \mathbb{P}\left[\chi^2_{n-1,\gamma_1}<V(X,\sigma^2)<\chi^2_{n-1,\gamma_2}\right] \\ & =\mathbb{P}\left[\chi^2_{n-1,\gamma_1}<\frac{n\hat{\sigma}^2}{\sigma^2}<\chi^2_{n-1,\gamma_2}\right] \\ & = \mathbb{P}\left[ r(\chi^2_{n-1,\gamma_2},X)<r\left(\frac{n\hat{\sigma}^2}{\sigma^2},X\right)<r(\chi^2_{n-1,\gamma_1},X)\right] \\ &=\mathbb P \left[ \underbrace{\dfrac{\sum{(X_i -\bar X_n)}^2}{\chi^2_{n-1,\gamma_2}}} _{A} <\sigma^2<\underbrace{\dfrac{\sum(X_i -\bar X_n) ^2}{\chi^2_{n-1,\gamma_1}}}_B\right] \\ &= 1-\alpha \end{align*}\]

Note como se tuvieron que invertir los extremos en \(\gamma_1\) y \(\gamma_2\). Esto es debido a que la función \(r\) es decreciente en \(v\). Siempre el valor más pequeño de \(r(v,x)\) debe ir a la izquiera y el más grande a la derecha.

Por lo tanto, el intervalo de confianza para \(\sigma^2\) al \(100(1-\alpha)\%\) es

\[ \Bigg[ \dfrac{\sum(X_i -\bar X_n) ^2}{\chi^2_{n-1,\gamma_2}}, \dfrac{\sum(X_i -\bar X_n) ^2}{\chi^2_{n-1,\gamma_1}}\Bigg].\]

Por ejemplo, si implementamos esto en R, tendríamos algo como lo siguiente:

set.seed(123)

X <- rnorm(n = 1000, 0, 2)
gamma1 <- 0.025
gamma2 <- 0.975
gamma2 - gamma1

[1] 0.95

(chi2_gamma1 <- qchisq(p = gamma1, df = 1000 - 1))

[1] 913.301

(chi2_gamma2 <- qchisq(p = gamma2, df = 1000 - 1))

[1] 1088.487

(diferencias <- sum((X-mean(X))^2))

[1] 3929.902

Finalmente el intervalo es

c(diferencias/chi2_gamma2, diferencias/chi2_gamma1)

[1] 4.047506 4.823884

Precaución

Las cantidades pivotales no siempre existen. Esto ocurre principalmente con las distribuciones discretas.

9.5 Transformaciones estabilizadoras de la varianza

9.5.1 Método Delta

El Método Delta es una herramienta poderosa en estadística que nos permite entender el comportamiento asintótico de transformaciones de estimadores consistentes y asintóticamente normales. Específicamente, nos ayuda a determinar cómo se distribuye una función de un estimador cuando el tamaño de la muestra tiende al infinito.

La pregunta clave es: ¿Cuál es el comportamiento de la distribución de \(\hat\theta\) cuando la muestra es grande?

Recordemos que si tenemos una muestra \(X_1,\dots, X_n\) que sigue una distribución normal \(N(\mu,\sigma^2)\) con \(\sigma^2\) conocida, entonces el estimador de máxima verosimilitud (MLE) de \(\mu\) es \(\hat\mu = \bar X_n\). Además, por el Teorema del Límite Central, sabemos que:

\[\begin{equation*} \frac{\bar X_n-\theta}{\frac{\sigma}{\sqrt{n}}} = \frac{\sqrt{n}(\bar X_n-\theta)}{\sigma} \xrightarrow{d} N(0,1) \end{equation*}\]

con

\[\begin{equation*} \mathrm{Var}(\bar X_n) = \frac{1}{n^2}\sum_{i=1}^n \mathrm{Var}(X_i) = \frac{\sigma^2}{n} \end{equation*}\]

Esto en general nos sugiera que si normalizamos un estadístico con su media y varianza, entonces la distribución de la normal estándar es una buena aproximación.

Ahora, el Método Delta específicamente dice que si \(g^{\prime}(\theta)\neq 0\) entonces

\[\begin{equation*} \frac{\sqrt{n}}{\sigma g^{\prime}(\theta)}[g(Y_n)-g(\theta)]\xrightarrow{d}N(0,1) \end{equation*}\]

Ejemplo 9.7 Consideremos el ejemplo de una muestra \(X_1,X_2,\dots\) i.i.d. de variables exponenciales con densidad \(f(x|\theta) = \frac{1}{\theta} e^{\frac{x}{\theta}}\). Entonces \(\mathbb{E}(X)=\theta\) y \(\mathrm{Var}(X)=\theta^2\). Se puede probar que el MLE \(\theta\) es \(\hat\theta = \bar X_n\) y que \(\mathrm{Var}(\bar X_n) = \frac{\theta^2}{n}\). Por lo tanto, el MLE es consistente. De acuerdo al Teorema del Límite Central, tenemos que:

\[\begin{equation*} \frac{\bar X_n-\theta}{\frac{\theta}{\sqrt{n}}} = \frac{\sqrt{n}(\bar X_n-\theta)}{\theta} \xrightarrow{d} N(0,1) \end{equation*}\]

o lo que es equivalente que

\[\begin{equation*} \bar{X}_n \xrightarrow{d} N\left(\theta,\frac{\theta^2}{n}\right) \end{equation*}\]

Si definimos \(g(\theta) = \dfrac{1}{\theta}\) entonces \(g^{\prime}(\theta) = -\dfrac{1}{\theta^2}\). Por lo tanto, el MLE de \(\dfrac{1}{\theta}\) es \(\dfrac{1}{\bar X_n}\). Estamos interesados en la distribución de \(\dfrac{1}{\bar X_n}\) cuando \(n\to\infty\). Por el Método Delta, tenemos que:

\[\begin{align*} \frac{\sqrt{n}}{\theta g^{\prime}(\theta)}[g(\bar X_n)-g(\theta)] & = \frac{\sqrt{n}}{\theta \frac{1}{\theta^2}}\left[\frac{1}{\bar X_n}-\frac{1}{\theta}\right] \\ & = \sqrt{n}\theta\left[\frac{1}{\bar X_n}-\frac{1}{\theta}\right] \xrightarrow{d} N(0,1) \end{align*}\]

En otras palabras

\[\begin{equation*} \frac{1}{\bar{X}_n} \xrightarrow{d} N\left(\frac{1}{\theta},\frac{1}{n\theta^2}\right). \end{equation*}\]

9.5.2 Aplicación del Método Delta para construir intervalos de confianza

Comencemos con este ejemplo y noten que en un punto no podremos avanzar en el desarrollo.

Ejemplo 9.8 Ssuponga que \(X_1,\dots, X_n\sim \text{Poisson}(\theta)\). Por propiedades del la Poisson, sabemos que \(\mu =\sigma^2 = \theta\). Suponga que se tiene suficientes datos para aproximar por una normal, entonces por el teorema del límite central, \[\sqrt n\dfrac{\bar X_n-\theta}{\sqrt{\theta}}\xrightarrow[]{d}N(0,1).\]

Entonces

\[\begin{align*} \mathbb P[|\bar X_n-\theta|<c] & = \mathbb P\bigg[\dfrac{\sqrt n|\bar X_n-\theta|}{\sqrt \theta}<\dfrac{c\sqrt n}{\sqrt \theta}\bigg] \\ & \approx 2\Phi\left(\dfrac{c\sqrt n}{\sqrt \theta}\right)-1. \end{align*}\]

Como consecuencia

\[\begin{equation*} \mathbb P\bigg[\bar X_n-\dfrac{c\sqrt \theta}{\sqrt n}<\theta<\bar X_n+\dfrac{c\sqrt \theta}{\sqrt n}\bigg]\approx 2\Phi\left(\dfrac{c\sqrt n}{\sqrt \theta}\right)-1. \end{equation*}\]

El problema acá es que no podemos avanzar más, pues no conocemos \(\theta\) y la varianza depende de este.

x_bar <- data.frame(n = numeric(), Z = numeric())

idx <- rep(x = c(10, 2000), times = 1000)
for (k in 1:length(idx)) {
muestra <- rpois(n = idx[k], lambda = 5)
x_bar[k, "Z"] <- sqrt(idx[k]) * (mean(muestra) - 5) / sqrt(5)
x_bar[k, "n"] <- idx[k]
}

ggplot(x_bar) +
geom_histogram(
mapping = aes(x = Z, y = after_stat(density)),
bins = 30,
color = "white"
) +
stat_function(
fun = dnorm,
args = list(mean = 0, sd = 1),
color = "red"
) +
facet_wrap(. ~ n, scales = "free") +
cowplot::theme_cowplot()

Observación. En este caso recuerden que \(\bar{X}_n\) es una variable aleatoria. Lo que dice el teorema del límite central es que conforme \(n\) es grande, la distribución de \(\bar{X}_n\) (centrada y escalada apropiadamente) converge a una normal estándar.

Nota

En las sección, hablamos de las cantidades pivotales, pero si ustedes lo notan, el estadístico todavía no se puede independizar de \(\theta\).

¿Qué se puede hacer en este caso? ¿Cómo transformar \(X_n\) para que tenga varianza constante?

Nota

El método Delta ya lo habíamos mencionado anteriormente. Se los resumo rápidamente.

Si \(X_1, \dots, X_n\) con cualquier distribución y \(T\) es un estimador tal que \(a_n(T-\theta) \to N(0,1)\), entonces \[ a_n \frac{(g(T) - g(\theta))}{g^{\prime}(\theta)} \to N(0,1) \]

Note que en el caso anterior se necesitaría saber explícitamente el valor desconocido de \(\theta\) para hacer el ejercicio.

Por el método Delta, la varianza “aproximada” de \(g(\bar X_n)\) es \[\left( \dfrac{g'(\mu)}{a_n}\right)^2 =\left( \dfrac{g'(\mu)\sigma}{\sqrt n}\right)^2 = \dfrac{g'(\mu)^2\sigma^2(\mu)}{n}.\] Si se desea que la varianza sea constante con respecto a \(\mu\),

\[\begin{align*} g'(u)^2\sigma^2(\mu) & = 1 \\ \implies g'(\mu) & = \dfrac{1}{\sigma(\mu)} \quad (\sigma(\mu)>0) \\ \implies g(\mu) & = \int_{a}^{\mu} \dfrac{dx}{\sigma(x)}dx \end{align*}\]

donde \(a\) es una constante arbitraria que hace la integral finita (y fácil de calcular).

Ejemplo 9.9 Del ejemplo anterior (Poisson), recuerde que \(\sigma ^{2} = \theta = \mu\), entonces se podría tomar que \(\sigma(\mu) = \sqrt{\mu}\) y por lo tanto definimos

\[ g(\mu) = \int_{0}^\mu\dfrac{dx}{\sqrt x} = 2\sqrt \mu \]

Por el método Delta, \[ 2\bar X_n^{\frac12} \underset{n \text{ grande}}{\sim} N\left(2\theta^{\frac 12},\dfrac1n\right) \]

De esta manera

\[\mathbb P[|2\bar X_n^{\frac12}-2\theta^{\frac12}|<c] =\mathbb P\Bigg[\dfrac{|2\bar X_n^{\frac12}-2\theta^{\frac12}|}{\sqrt{1/n}}<\sqrt nc\Bigg] \approx 2\Phi(\sqrt nc)-1 \]

Desarrollando, \[\mathbb P[-c+2\bar X_n^{\frac12}<2\theta^{\frac 12}<c+2\bar X_n^{\frac12}]\approx 2\Phi(\sqrt nc)-1 \]

Se despeja \(c\) tal que \[\Phi(\sqrt n c) = 1-\frac{\alpha}{2}\implies c = \dfrac 1{\sqrt n} z_{1-\frac{\alpha}{2}}.\]

El intervalo para \(2\theta^{\frac 12}\) es \[\bigg[2\bar X_n^{\frac 12} -\dfrac 1{\sqrt n} z_{1-\frac{\alpha}{2}},2\bar X_n^{\frac 12} +\dfrac 1{\sqrt n} z_{1-\frac{\alpha}{2}}\bigg]\]

set.seed(42)
X <- rpois(n = 1000, lambda = 5)
x_bar <- mean(X)
z <- qnorm(p = 0.975)

c(
2 * sqrt(x_bar) - 1 / sqrt(1000) * z,
2 * sqrt(x_bar) + 1 / sqrt(1000) * z
)

[1] 4.371529 4.495488

Para estimar el IC para \(\theta\), vea que si \(y=2x^{\frac12} \implies x = \dfrac{y^2}{4}\). Aplicando esta transformación al intervalo anterior, se obtiene

\[\bigg[\dfrac 14 \left(2\bar X_n^{\frac 12} -\dfrac 1{\sqrt n} z_{1-\frac{\alpha}{2}}\right)^2,\dfrac 14 \left(2\bar X_n^{\frac 12} +\dfrac 1{\sqrt n} z_{1-\frac{\alpha}{2}}\right)^2\bigg].\]

c(
(1 / 4) * (2 * sqrt(x_bar) - 1 / sqrt(1000) * z)^2,
(1 / 4) * (2 * sqrt(x_bar) + 1 / sqrt(1000) * z)^2
)

[1] 4.777567 5.052354